概要
SARIMAではなく、SRIMA"X"というモデルを使って、祝休日データを説明変数に加えて東京都のコロナ感染者数を予測させてみました。
SARIMAでは予測したいデータ$y_t$そのものの過去の傾向を学習して予測してくれるモデルですが、祝休日やそのほかのイベント情報を学習に組み込むことができません。そこで、SARIMAXでは、複数時系列データを扱えるように拡張したモデルとなっています。(似ているものとして、ARIMAXがあります。)
こちらの記事(SARIMAを使ったコロナ感染者数を予測)の続きです
書いているコードはSRAIMAとほぼ同じなので、前回の記事を参考にしていただきつつ、相違点だけをこちらで記載するようにします。
利用するライブラリ
使用しているライブラリは、次の通りです。SARIMAを作った時からjpholiday というライブラリを加えている程度です。
jpholiday
statsmodels
pandas
numpy
matplotlib
datetime
ライブラリの入れ方
pipで入れることができます。
pip install statsmodels
pip install jpholiday
祝休日を説明変数として加える
import jpholiday
# 土日判定をするために、weekdayを取得する
df_tokyo["weekday"] = df_tokyo["Date"].dt.weekday
# holidayの判定をするためのカラムを初期化
df_tokyo["holiday"] = False
list_holiday = []
# 祝日の判定
for i in range(df_tokyo.shape[0]):
date = df_tokyo.iloc[i,0]
is_holiday = jpholiday.is_holiday(date)
list_holiday.append(is_holiday)
df_tokyo["holiday"] = list_holiday
df_tokyo["holiday"].mask(df_tokyo["weekday"] == 5, True, inplace=True)
df_tokyo["holiday"].mask(df_tokyo["weekday"] == 6, True, inplace=True)
del df_tokyo["weekday"]
df_tokyo
コードを説明します。
コードの流れは、
- まず土日判定のために"weekday"カラムを作る。
- 祝日判定のための"holiday"というカラムを初期化して追加する
- 1日毎に日付を読み込み祝日判定し、祝日なら"True"、祝日以外は"False"が入るようにする
- weekdayカラムの中で"5"と"6"がそれぞれ土曜と日曜なので、"holiday"カラムにTrueを入れるようにする。
- weekdayカラムが不要なので、削除する
1:まず土日判定のために"weekday"カラムを作る。
# 土日判定をするために、weekdayを取得する
df_tokyo["weekday"] = df_tokyo["Date"].dt.weekday
2:祝日判定のための"holiday"というカラムを初期化して追加する
# holidayの判定をするためのカラムを初期化
df_tokyo["holiday"] = False
3:1日毎に日付を読み込み祝日判定し、祝日なら"True"、祝日以外は"False"が入るようにする
list_holiday = []
# 祝日の判定
for i in range(df_tokyo.shape[0]):
date = df_tokyo.iloc[i,0]
is_holiday = jpholiday.is_holiday(date)
list_holiday.append(is_holiday)
df_tokyo["holiday"] = list_holiday
4:weekdayカラムの中で"5"と"6"がそれぞれ土曜と日曜なので、"holiday"カラムにTrueを入れるようにする。
df_tokyo["holiday"].mask(df_tokyo["weekday"] == 5, True, inplace=True)
df_tokyo["holiday"].mask(df_tokyo["weekday"] == 6, True, inplace=True)
5:weekdayカラムが不要なので、削除する
del df_tokyo["weekday"]
SRAIMAの最適パラメータ探索
祝休日データを含めてSARIMAを構築する時は、外部説明変数を明示する必要があります。
パラメータ自体は、前回と同様にまずはARIMAを構築し、残りのパラメータ$(P,D,Q)$をグリッドサーチで探索し、基準としては$BIC$を使って探索します。
best_param_seasonal = [0,0,0,0]
best_bic = 100000
best_param = (4,1,2)
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(endog = ts, # 予測したい変数 y_t
exog = ts_holiday, # 外部説明変数
order = best_param,
seasonal_order = param_seasonal,
enforce_stationarity = False,
enforce_invertibility = False)
results = mod.fit()
print('ARIMA{}x{}7 - BIC:{}'.format(best_param, param_seasonal, results.bic))
if best_bic > results.bic:
best_param_seasonal = param_seasonal
best_bic = results.bic
except:
continue
print('*BEST ARIMA{}x{}7 - BIC:{}'.format(best_param, best_param_seasonal, best_bic))
実行した結果、SARIMAのパラメータは$(p,d,q)(P,D,Q)[s] = (4,1,2)(3,0,0)[7]$ となりました。祝休日を考慮せずにモデルを構築した時のパラメータは$(4,1,2)(3,1,3)[7]$だったので、だいぶパラメータが変わりました。
SRIMAXの構築
上記の最適パラメータ探索の結果を使い、SRIMAXモデルの学習をさせます。
先ほどの最適パラメータ探索と同様、外部説明変数を明示させて、モデルの構築、学習をさせます。
sarima_model = sm.tsa.SARIMAX(endog = ts,
exog = ts_holiday,
order=best_param,
seasonal_order=best_param_seasonal).fit()
検証データを使って、予測する。
SARIMAを使った時とは違い、予測には、get_predictionメソッドを使います。
(SARIMAの時は、predictメソッドを使っていました。)
min_date = x_test.index.min()
max_date = x_test.index.max()
predict = sarima_model.get_prediction(start = min_date,
end = max_date,
exog = ts_holiday_test)
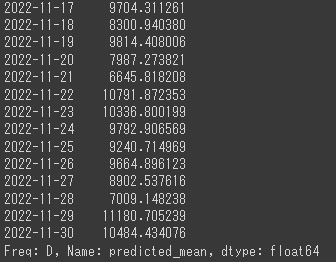
predict_value = predict.predicted_mean
display(predict_value)
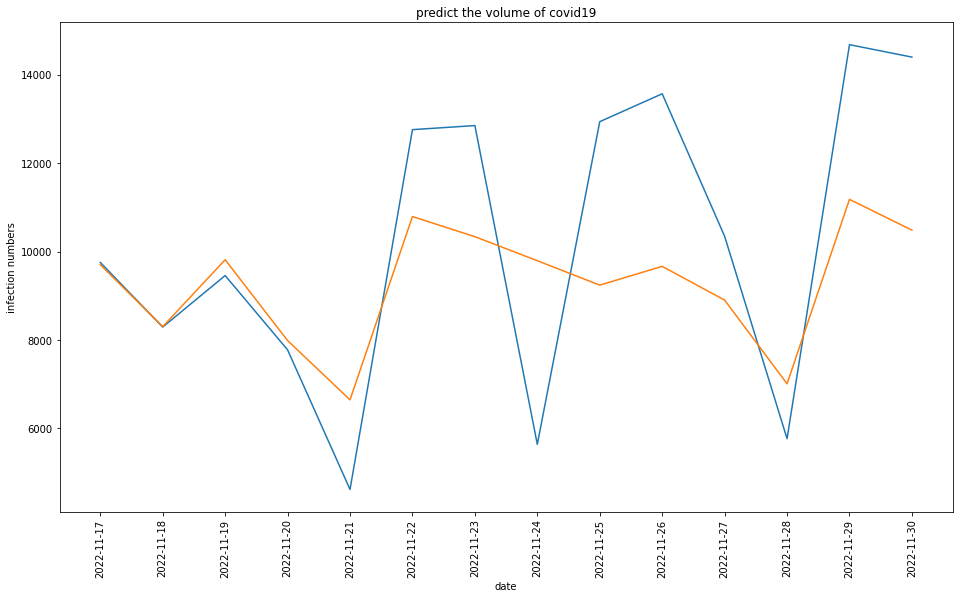
実際の感染者数のデータと予測したデータをそれぞれグラフにプロットさせます。
# 訓練データ・検証データ全体のグラフ化
fig, ax = plt.subplots(figsize=(16,9))
# データのプロット
plt.plot(x_test.index, x_test['Tokyo']) # 実データをプロット
plt.plot(predict_value) # 予測データをプロット
# 日付表記を90度回転
ax.tick_params(axis='x', rotation=90)
locator = mdates.DayLocator(interval=1)
ax.xaxis.set_major_locator(locator)
# titleなど
ax.set_title('predict the volume of covid19')
ax.set_xlabel('date')
ax.set_ylabel('infection numbers')
plt.show()
最初の3日間ほどはかなりの精度で予測できていて、それ以降のズレが大きくなっている点はSARIMAと同じです。
注目したい点は、11月24日の数値です。前回のSARIMAでは、祝日直後の11月24日のズレが大きく精度が下がってしまっていました。だから、祝休日情報を含めて学習させることができるSARIMAXを今回試してみたわけですが、結果はあまり変わらず、祝日成分をあまり反映できていないように見えます。
MAPEの計算
実際に精度が上がったのか下がったのか指標で計算してみましょう。
def Mape(predict, observed):
absolute_diff_percentage = abs( (predict - observed) / observed)
sum_abs_diff = sum(absolute_diff_percentage)
mape = sum_abs_diff / len(predict)
return mape
mape = Mape(predict_value, x_test["Tokyo"].values)
print("mape : " + str(mape * 100) + " %")
$MAPE = 約21.7%$となりました。
あれ、SARIMAよりも精度が下がってしまいました。。。
「祝日情報を反映させられれば、精度が向上するのでは?」という期待が大きいかっただけに裏切られる結果になってしまいました。
まとめと考察
前回のSARIMAでコロナ感染者数を予測の結果から、祝休日情報を反映させることができれば、コロナ感染者数の予測精度が高まると考えていましたが、結果はそれと反対になってしまいました。
精度向上策としては考えていることは、「祝休日情報にラグを加える」ということです。
感染検査を受ける人の行動を考慮するためにはラグを加えるべきだと考えています。おそらく、感染の検査を受けるのは主に祝休日だと思うので、祝休日明け直後に検査を受ける人が少なくなる、という傾向を捉えるために、祝休日情報を1つまたは2つラグでずらしてあげることで精度が上がるのではないでしょうか?
精度があまり出なかった要因や精度向上策がほかにあれば、コメント等で教えていただけると嬉しいです。
参考にしたページ
今回は次のページを参考にさせていただきました。