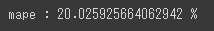【python】SARIMAを使って東京都のコロナ感染者数を予測する

概要

時系列モデルである『SARIMA』を使ってコロナ感染者数を予測してみました。
コロナ感染者数に限らず、時系列データ（特に季節変動があるようなデータ）であれば、同じように時系列データの予測をすることができます。

コロナ感染者数のデータは厚生労働省が発表しているオープンデータを使います。
厚生労働省のコロナ感染者数データ（リンクをクリックするとcsvをダウンロードします。）

コード全文はGithubにアップロードしているので、そちらを見てください。

利用するライブラリ

主に使っているライブラリは下の5つです。他にもライブラリを使っていますが、コードを見ていただければと思いますが、基本的には下の5個を使っています。

statsmodels
pandas
numpy
matplotlib
datetime

ライブラリの入れ方

pipで入れることができます。

pip install statsmodels

コロナ感染者数の予測

ライブラリのインポート

# 必要ライブラリのimport
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import statsmodels.api as sm

import matplotlib.dates as dates
import datetime as dt
from datetime import datetime
import matplotlib.dates as mdates
import math
import itertools
import pandas.tseries.offsets as offsets

データの読み込み

# 厚生労働省の公開データ
url = 'https://covid19.mhlw.go.jp/public/opendata/newly_confirmed_cases_daily.csv'

# データ読み込み
df = pd.read_csv(url, parse_dates=[0])

# 結果確認
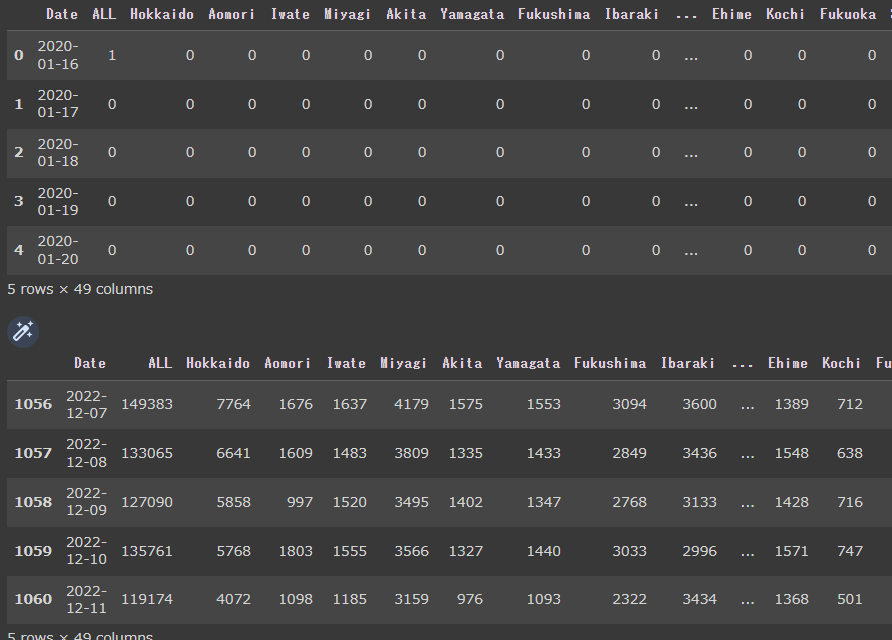
display(df.head())

display(df.tail())
   

出力結果はこちら。

都道府県別に20年1月16日から22年12月11日までのデータが格納されています（コードを作成した日時が12月12日なので、その前日の12月11日までのデータが入っているようです）。

データの期間を調整

後日、アップロードする予定の記事内容で検証したいことがあるので、あえてデータの期間を22年11月30日までにします。

検証したいこと：祝休日の情報を学習データに入れた方が予測精度が上がるのではないか？という仮説の検証です。今回の記事では、素直にコロナ感染者数のデータのみでモデルの学習・予測をさせ、祝休日情報を入れた場合との精度比較ができれば、という意図です。

データの整形

今回の予測対象は東京都のコロナ感染者数を予測したいので、まず東京のコロナ感染者数のみを抽出します。そのあと、学習データと検証データに分割します。

1. 東京のコロナ感染者数の予測を実施するので、東京コロナ感染者に絞り込む。
2. 予測日数を14日間として、データを学習データと検証用データに分割する。

# 東京のデータだけに絞り込み
df_tokyo = df[["Date", "Tokyo"]]


# 分割日 mdayの設定 (最終日から14日前)
mday = df_tokyo['Date'].iloc[-1] - offsets.Day(14)


# 訓練用indexと検証用indexを作る
train_index = df_tokyo['Date'] <= mday
test_index  = df_tokyo['Date'] > mday


# 入力データの分割
x_train = df_tokyo[train_index]
x_test  = df_tokyo[test_index]

x_train = x_train.set_index('Date')
ts      = x_train['Tokyo']

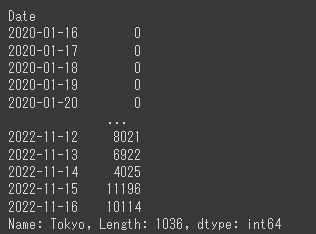
display(ts)

出力結果。

データの可視化

ここで、コロナ感染者数のデータを可視化してみます。
ただ可視化するのではなく、成分分解したデータを表示してみます。

成分分解：時系列データ = トレンド + 季節変動 + 残差

res = sm.tsa.seasonal_decompose(ts, period=14)
fig = res.plot()
fig.set_size_inches(16,8)
fig.tight_layout()

実行結果。

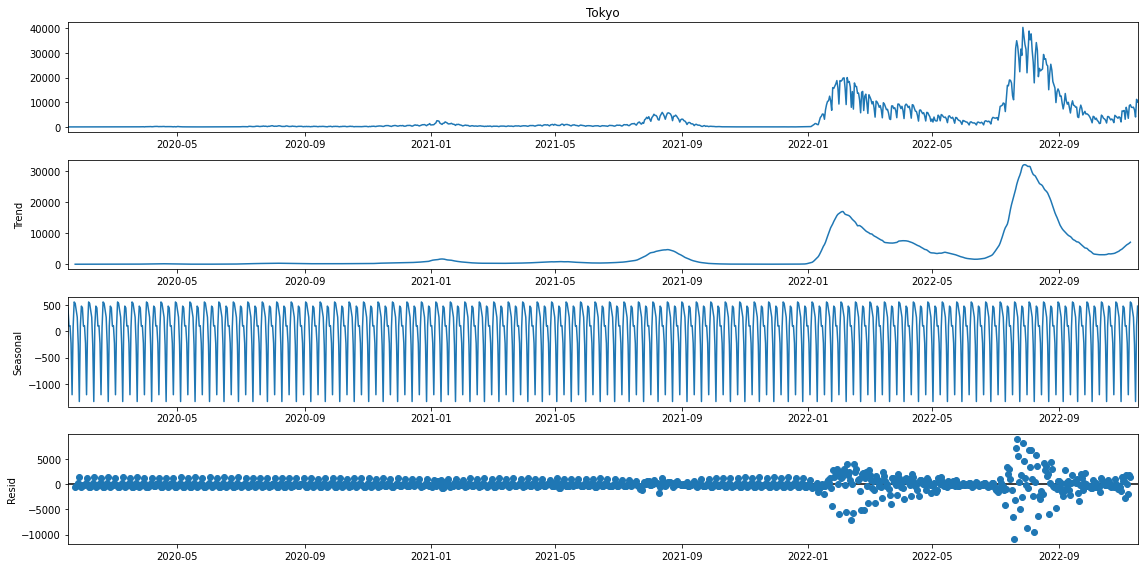
まず生データに注目します（一番上のグラフ）。マクロにデータを見ると、いわゆる第〇波と呼ばれるような大きな増減の山がいくつかあり、ミクロにみると、周期的な変動があるように見えます。

上から2番目のトレンド（trend）をみると、その第〇波に合わせて増減していることを捉えたグラフになっています。

上から3番目のグラフは、季節変動（周期変動）のグラフです。似通った形の細かいグラフが繰り返されている様子を確認できます。

一番下のグラフは残差を表しており、トレンドと季節変動でとらえることができない成分を表しているデータです。

まず着目したいのが、seasonal（季節変動）のデータです。どのくらいの周期で増減を繰り返しているのかを確認してみます。

ts_check  = ts.loc['2022/10/1':'2022/11/1']
res_check = sm.tsa.seasonal_decompose(ts_check)

fig    = res_check.plot()
fig.set_size_inches(16,9)
fig.tight_layout()

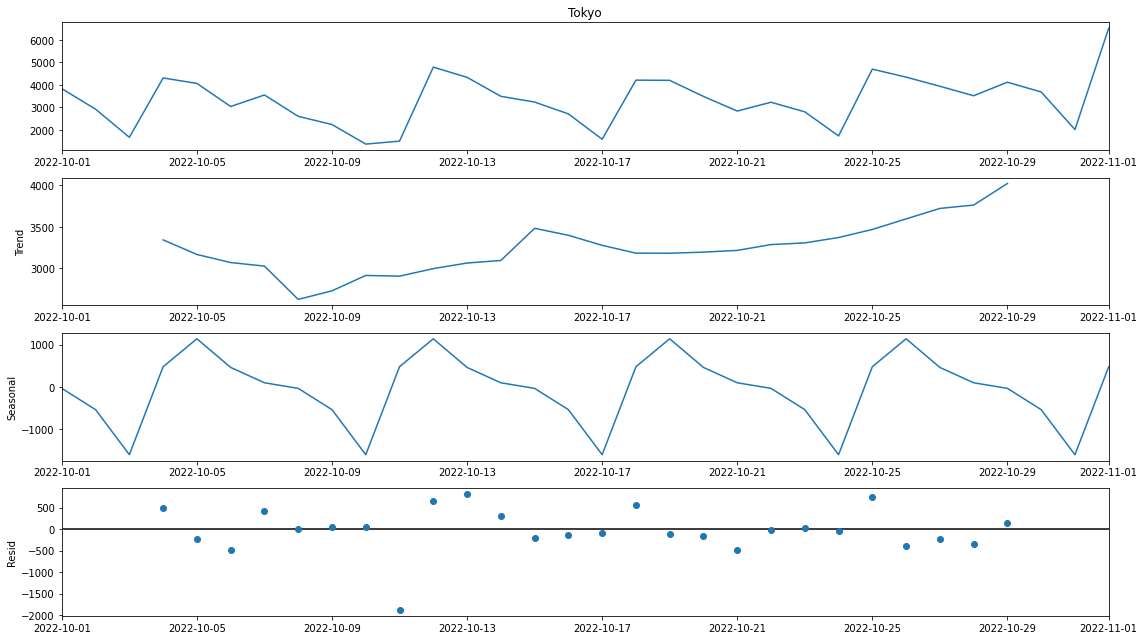
だいたい7日周期になっていることを確認できます。ちゃんと確認してみましょう。

# 初日(22年10月1日)の感染者数を抽出
val = res_check.seasonal[0]

fig, ax = plt.subplots(figsize=(16, 9))

# インデックスを日時にする
res_check.index = pd.to_datetime(ts_check.index)

# データをプロットする
ax.plot(res_check.index, res_check.seasonal)

# グラフのフォーマットなどの調整
formatter = mdates.DateFormatter("%m/%d")
locator   = mdates.DayLocator()
ax.xaxis.set_major_formatter(formatter)
ax.xaxis.set_major_locator(locator)
fig.autofmt_xdate(rotation=90, ha="center")

# y=val(10月1日の値）に水平線を引く
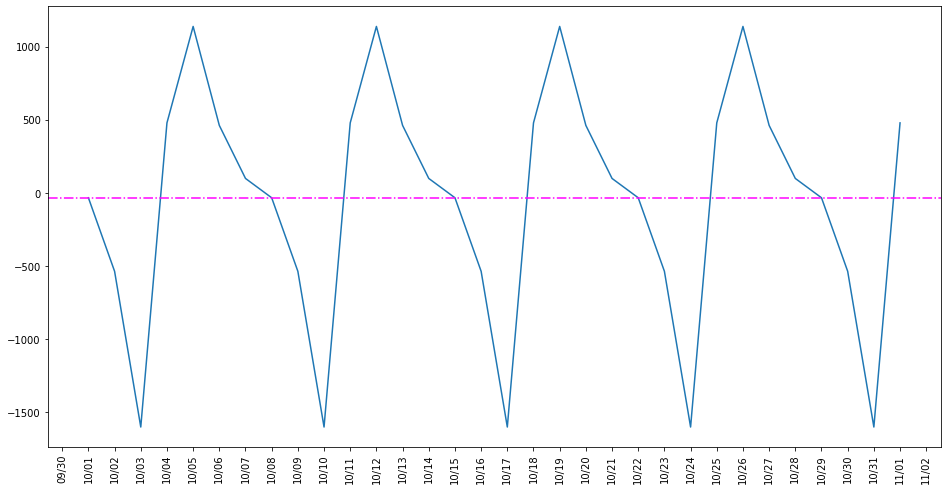
plt.axhline(val, ls = "-.", color = "magenta")

plt.show()

初日(今回は22年10月1日)のデータから横方向に点線を引いてどのくらいの周期があるのかをわかりやすくしてみました。

結果、7日周期のデータであることを確認できます。
（後で出てきますが、この周期がSARIMAの成分$SARIMA(p,d,q)(P,D,Q)[s]$の"s"に該当しますので、この確認は結構重要です。）

自己相関、偏自己相関を描く（コレログラム）

時系列データといえば、これですよね。自己相関、偏自己相関を描きます。これを描くことで、相関係数という指標を使って、データの周期性を確認することができます。

#コレログラム
_, axes = plt.subplots(nrows=2, ncols=3, figsize=(16, 12))

# 原系列の ACF
sm.tsa.graphics.plot_acf(ts, ax=axes[0][0])
# 原系列の PACF
sm.tsa.graphics.plot_pacf(ts, ax=axes[1][0])

# 残差の ACF
sm.tsa.graphics.plot_acf(res.resid.dropna(), ax=axes[0][1])
# 残差の PACF
sm.tsa.graphics.plot_pacf(res.resid.dropna(), ax=axes[1][1])

# 1次の階差系列の ACF
sm.tsa.graphics.plot_acf(ts.diff(1).dropna(), ax=axes[0][2])
# 1次の階差系列の PACF
sm.tsa.graphics.plot_pacf(ts.diff(1).dropna(), ax=axes[1][2])

# グラフを表示する
plt.show()

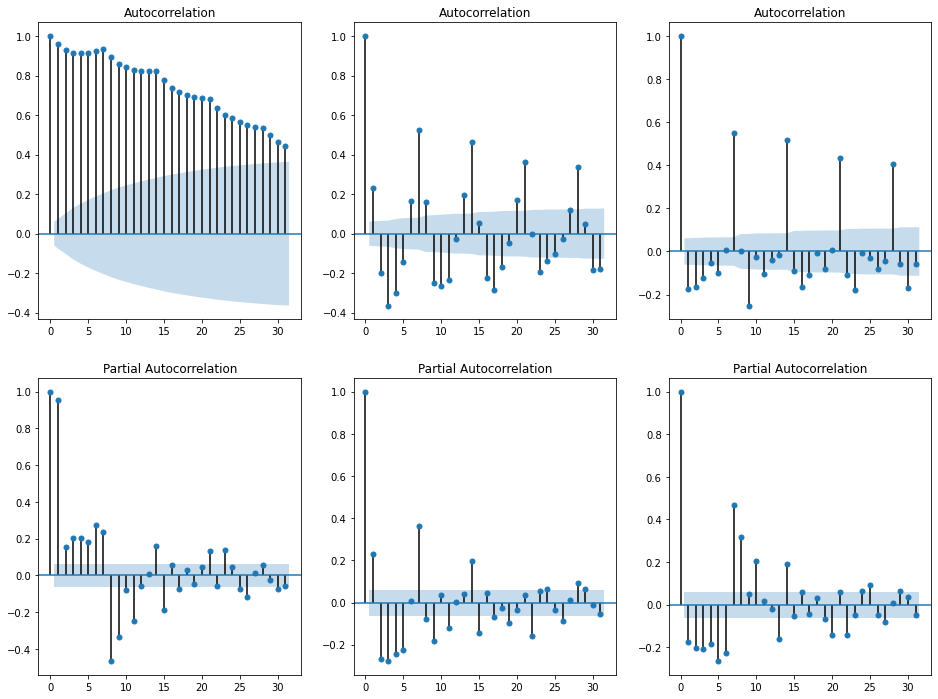
• 左：原系列(オリジナルデータ)
• 真ん中：残差系列
• 右：1次階差系列のデータ

です。

どのデータも、自己相関係数を見ると、7日周期であることを確認できます。
また、1次の階差系列データの偏自己相関(右下)を見ても7日周期であることを確認できます。

ADF検定

単位根過程であるかどうかを確認するために、ADF検定を実施します。今回は、原系列のデータと1次階差系列データのそれぞれでADF検定を実施します。

期待としては、原系列データは非定常で、1次階差系列データは定常となっていることを期待しています。

print("-------------原系列--------------")
# トレンド項なし、定数項なし
nc = sm.tsa.stattools.adfuller(ts, regression="nc")
# トレンド項なし、定数項あり
c = sm.tsa.stattools.adfuller(ts, regression="c")
# トレンド項あり（1次まで）、定数項あり
ct = sm.tsa.stattools.adfuller(ts, regression="ct")
# トレンド項あり（1次+非線形トレンド）、定数項あり
ctt = sm.tsa.stattools.adfuller(ts, regression="ctt")

print("nc  p-value:" + str(nc[1]))
print("c   p-value:" + str(c[1]))
print("ct  p-value:" + str(ct[1]))
print("ctt p-value:" + str(ctt[1]))


print()
print("-------------1次階差系列--------------")
ts_diff = ts.diff().dropna()

# トレンド項なし、定数項なし
nc = sm.tsa.stattools.adfuller(ts_diff, regression="nc")
# トレンド項なし、定数項あり
c = sm.tsa.stattools.adfuller(ts_diff, regression="c")
# トレンド項あり（1次まで）、定数項あり
ct = sm.tsa.stattools.adfuller(ts_diff, regression="ct")
# トレンド項あり（1次+非線形トレンド）、定数項あり
ctt = sm.tsa.stattools.adfuller(ts_diff, regression="ctt")

print("nc  p-value:" + str(nc[1]))
print("c   p-value:" + str(c[1]))
print("ct  p-value:" + str(ct[1]))
print("ctt p-value:" + str(ctt[1]))

あれ？おかしい。。
原系列データではp値が5%以上になっていることを期待（≒非定常データ）していたのですが、ADF検定をしたらすべてが定常であることを示す結果になってしまいました。
1次階差系列のデータは期待通りにp値が5%よりも小さいので、定常データと言えそうです。

解釈に困りますが、ここはいったん無理やり、コロナ感染者数のデータは単位根過程である、と仮定したまま分析を進めることにします。

ARIMAモデルの構築

ここは工夫ポイント1です。いきなりSARIMAを構築するのではなく、まずはARIMAモデルを構築することにします。ARIMAモデルでは、3つのパラメータ$(p,d,q)$を決定する必要がありますが、ADF検定で実施したように1次階差系列のデータが定常過程となることを確認できているので、$d=1$としてモデルを構築することにします。

ARMAモデルの構築

ここは工夫ポイント2です。上記したように、ARIMAのパラメータ$(p,d,q)$は$d=1$であることがわかっているので、1次階差系列に対して、ARMAモデルを構築することにします。

ARMAモデルの最適パラメータの探索

1次階差系列に対して$ARMA(p,q)$の最適パラメータを探索します。ここでは、statsmodelのメソッドを使い、基準として$BIC$を使うことにします。

# トレンド項なし、定数項なし
params2 = sm.tsa.arma_order_select_ic(ts.diff().dropna(), ic='bic')
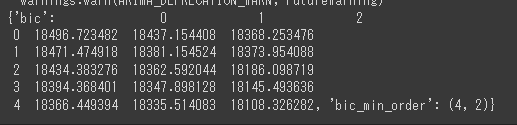
params2

実行結果。

いろいろと警告(warning)が出ますが、最適パラメータは$(p,q) = (4,2)$であることを確認できました。

結果、構築したかったARIMAのパラメータは$(p,d,q) = (4,1,2)$となります。

SARIMAの最適パラメータ探索

ARIMAモデルのパラメータが決まったので、次は本命のSARIMAのパラメータを探索します。SARIMAのパラメータは$(p,d,q)(P,D,Q)[s]$の合計7個ありますが、最初に確認した周期性7日間(="s")、先ほど構築したARIMAのパラメータ$(p,d,q) = (4,1,2)$はすでに分かっているので、実質探索すべきパラメータの数は$(P,D,Q)$の3つのみです。

いきなりSARIMAを作るのではなく、ARIMAモデルを構築して丁寧にパラメータ探索をしたおかげで、7個のパラメータの探索をする必要がなくなり、組み合わせ爆発問題を回避して、最適パラメータ探索時間を大幅に減らすことができました。

パラメータ自体はグリッドサーチで行い、基準は$BIC$で最適化します。

# SARIMAのseasonal成分のパラメータを推定するために、各パラメータのパターンを作る
p = range(0, 4)
d = range(0, 4)
q = range(0, 4)
pdq = list(itertools.product(p, d, q))

# '7'は周期性が明らかに7だから決め打ちで設定している。
seasonal_pdq = [(x[0], x[1], x[2], 7) for x in list(itertools.product(p, d, q))]

best_param_seasonal = [0,0,0,0]
best_bic = 100000

best_param = (4,1,2)

for param_seasonal in seasonal_pdq:
  try:
    mod = sm.tsa.statespace.SARIMAX(ts,
                                    order = best_param,
                                    seasonal_order = param_seasonal,
                                    enforce_stationarity = False,
                                    enforce_invertibility = False)
    results = mod.fit()
    print('ARIMA{}x{}7 - BIC:{}'.format(best_param, param_seasonal, results.bic))
    
    if best_bic > results.bic:
        best_param_seasonal = param_seasonal
        best_bic = results.bic
  
  except:
    continue
print('*BEST ARIMA{}x{}7 - BIC:{}'.format(best_param, best_param_seasonal, best_bic))

実行結果。

Google Colaboratoryで実行すると少し時間がかかりましたが、最適なパラメータを探索することができました。

結果、$SARIMA(p,d,q)(P,D,Q)[s] = SARIMA(4,1,2)(3,1,3)[7]$

SARIMAの構築

上記で探索したパラメータを使って、モデルを構築します。

sarima_model = sm.tsa.SARIMAX(ts, order=best_param, seasonal_order=best_param_seasonal).fit()

検証データを使って感染者数を予測する

検証期間に対して、構築したSARIMAで予測させます。

min_date = x_test['Date'].min()
max_date = x_test['Date'].max()

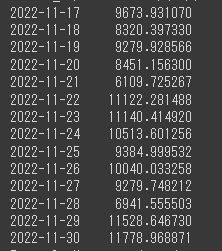
predict = sarima_model.predict(min_date, max_date)

display(predict)

実行結果。

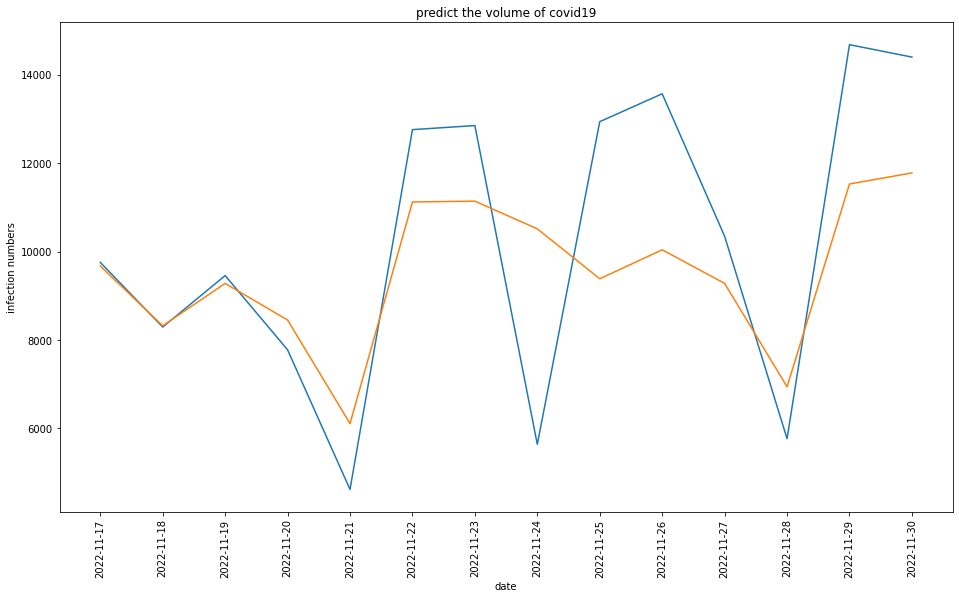
実際の感染者数のデータと予測したデータをそれぞれグラフにプロットさせます。

# 訓練データ・検証データ全体のグラフ化
fig, ax = plt.subplots(figsize=(16,9))

# データのプロット
plt.plot(x_test['Date'], x_test['Tokyo'])  # 実データをプロット
plt.plot(predict)  # 予測データをプロット


# 日付表記を90度回転
ax.tick_params(axis='x', rotation=90)

locator = mdates.DayLocator(interval=1)
ax.xaxis.set_major_locator(locator)

# titleなど
ax.set_title('predict the volume of covid19')
ax.set_xlabel('date')
ax.set_ylabel('infection numbers')


plt.show()

結果、最初の3日間ほどはかなり良い精度で予測できていますが、徐々に誤差が大きくなっていってます。ただ、見方を変えると、増える/減るタイミングはある程度捉えることができており、絶対値的な誤差はあれども増減傾向を捉えることをできているモデルだと言えると思います。

MAPEの計算

上記では、グラフを見て定性的に精度の評価をしましたが、次はちゃんと定量的に精度評価を実施します。

今回は時系列データの予測でよく使われているMAPEという指標で精度を確認します。

MAPE = Mean Abolute Percentage Error（平均絶対パーセント誤差）

MAPEを計算する関数を定義。

def Mape(predict, observed):
  absolute_diff_percentage =  abs( (predict - observed) / observed)
  sum_abs_diff = sum(absolute_diff_percentage)
  mape = sum_abs_diff / len(predict)

  return mape

mape = Mape(predict, x_test["Tokyo"].values)

print("mape : " + str(mape * 100) + " %")

実行結果。

MAPE = 約20%

20%という値を大きいと考えるか、小さいと考えるかはその目的や感性に依存するかと思いますが、筆者は次のように考えています。

「予測精度自体はそこまで高くないものの、上記したように増減傾向自体はある程度捉えることができているので、コロナ感染者数の増減に応じて何らかの対策や打ち手をうつときの参考情報としては十分使えるモデル。」

まとめと考察

今回はSARIMAを使って、東京都のコロナ感染者数を予測させてみました。結果、MAPEで約20%の精度でした。

精度を向上させる方法として、

1. 祝休日の情報を加える。今回の予測モデルで大きな誤差を生んでいるのが22年11月24日でした。実は22年11月23日が祝日だったので、その情報を加えることで精度を向上させることができるかもしれません。（祝休日情報を説明変数として予測させるのは次回実施してみようと思います。）
2. 学習期間を直近のみにする。今回は20年1月16日から22年11月16日までを学習データとしましたが、これをもっと直近の期間にすることも方法としてあると思います。20年、21年のコロナ感染者数の傾向は22年のそれと異なっていると思います。傾向の異なるデータを学習してしまったので、22年11月後半の感染者数の傾向を捉えることができなかったのかもしれません。

他にも、ニューラルネットワークをベースにした時系列予測や、深層学習を使った予測モデルにするなどいろいろと精度向上させる方法があり得ると思いますが、いったんはこんなところかなと考えています。

他にも精度を上げる方法があればコメントなどで教えていただけると嬉しいです。

次回はSARIMAXモデルを使って祝休日情報を組み込んで予測させてみます。

参考にしたページ

今回はここのレポートを大いに参考にさせていただきました。