こんにちは。
前回の記事ではデータをimportしたり、データの中身を確認してみたりしました。
今回は実際にモデルを作成し、その精度等を確認してみたいと思います。
今回使うデータはStore Item Demand Forecasting Challengeを使いたいと思います。
データの詳細について今回は省略します。
時系列データなので、FBprophetというライブラリを利用したいと思います。
データの準備
まずは上記ページからCSVデータをダウンロードし、DataBricks上にアップロードします。
これらの方法は前回の記事を参照してください。
ファイルはData内の/FileStore/testdata/train.csvとしてアップロードしました。
fbprophetのインストール
今回利用するライブラリをインストールします。
自分はここで詰まってしまったのですが、前提ライブラリの最新版に対応していないことが問題だったので、そこのダウングレードを一緒に行っています。
!echo y | %pip uninstall pystan
%pip install pystan==2.19.1.1
%pip install fbprophet
これで必要な準備はできました。
モデルの作成
まずモデルを作成するために使うデータをimportします。
from pyspark.sql.types import *
# 今回利用するデータのスキーマを指定 (型修正オプションで自動読み取りも可能)
schema = StructType([
StructField("date", DateType(), False),
StructField("store", IntegerType(), False),
StructField("item", IntegerType(), False),
StructField("sales", IntegerType(), False)
])
# FileStore に格納されているCSVを読み込み
inputDF = spark.read.format("csv")\
.options(header="true", inferSchema="true")\
.load("/FileStore/testdata/train.csv", schema=schema)
# クエリを発行可能な状態にするために、一時ビューを作成
inputDF.createOrReplaceTempView('history')
history = inputDF
# Spark3.0以降だとDATE_FORMATがうまく動作しないので、timeParserPolicyをLEGACYにすることで対応する
spark.sql("set spark.sql.legacy.timeParserPolicy=LEGACY")
続いて、作成するモデルの定義を行います。
# モデルの定義
def define_prophet_model(params):
model = Prophet(
interval_width=params["interval_width"], # 信頼区間
growth=params["growth"], # モデルの種類。線形回帰(linear)またはロジスティック回帰(logistic)
daily_seasonality=params["daily_seasonality"], # 日ごとの周期性の有無
weekly_seasonality=params["weekly_seasonality"], # 月ごとの周期性の有無
yearly_seasonality=params["yearly_seasonality"], # 年ごとの周期性の有無
seasonality_mode=params["seasonality_mode"] # 周期性の傾向
)
return model
# 予測
def make_predictions(model, number_of_days):
return model.make_future_dataframe(periods=number_of_days, freq='d', include_history=True)
実際にモデルを作成します。
from pyspark.sql.functions import to_date, col
from pyspark.sql.types import IntegerType
# 学習用の pandas df を用意
history_sample = history.where(col("date") >= "2015-01-01").sample(fraction=0.01, seed=123)
history_pd = history_sample.toPandas().rename(columns={'date':'ds', 'sales':'y'})[['ds','y']]
# fbprophetを利用した場合のメッセージを非表示に
import logging
logging.getLogger('py4j').setLevel(logging.ERROR)
# モデルの定義
from fbprophet import Prophet
params = {
"interval_width": 0.95, # 信頼区間95%
"growth": "linear", # 線形回帰
"daily_seasonality": False, # 日ごとの周期性なし
"weekly_seasonality": True, # 月ごとの周期性あり
"yearly_seasonality": True, # 年ごとの周期性あり
"seasonality_mode": "multiplicative" # 周期性を増加させていく
}
model = define_prophet_model(params)
# 過去のデータをモデルに学習させる
model.fit(history_pd)
これでモデルを作成することができました。
実際にモデルの精度を確認してみたいと思います。
モデルの確認
まずは実際に予測してみたいと思います。
# 過去のデータと先90日間を含むデータフレームを定義
future_pd = model.make_future_dataframe(
periods=90,
freq='d',
include_history=True
)
# データセット全体に対して予測実行
forecast_pd = model.predict(future_pd)
display(forecast_pd)
実際に予測を行い、その結果がforecast_pd内に格納されます。
上記では表形式で表示されていると思うので、グラフにして視覚化したいと思います。
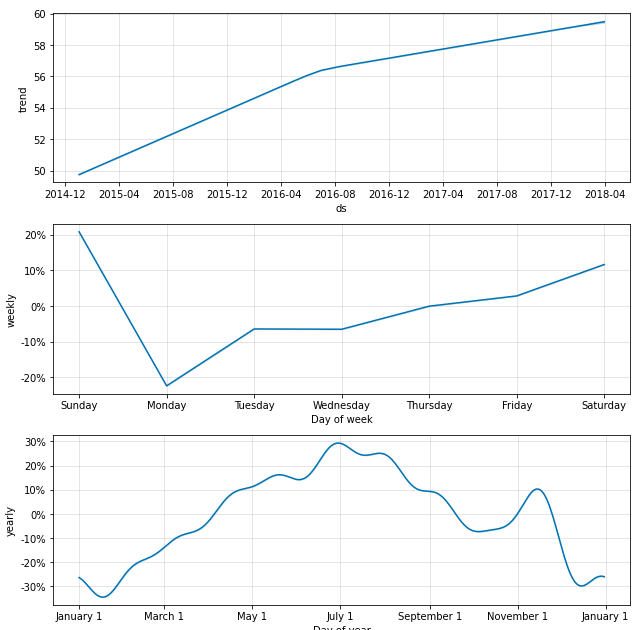
trends_fig = model.plot_components(forecast_pd)
display(trends_fig)
1つ目のグラフは販売数の推移を表しています。16年8月以降上昇が鈍化しています。
2つ目のグラフは1週間の周期性を表しています。月曜に販売数が落ち、土日に向けて上昇していることがわかります。
3つ目のグラフは年単位の周期性を表しています。夏に向かい上昇し、冬に向かい減少するという大まかな傾向がわかります。
傾向については上記で確認できました。
続いて、実際の予測値がどのようになっているかを視覚化してみたいと思います。
わかりやすいように過去一年の予測結果のみ表示してみます。
predict_fig = model.plot( forecast_pd, xlabel='date', ylabel='sales')
# 出力されるデータを過去1年と予測機関のみに絞る
xlim = predict_fig.axes[0].get_xlim()
new_xlim = ( xlim[1]-(180.0+365.0), xlim[1]-90.0)
predict_fig.axes[0].set_xlim(new_xlim)
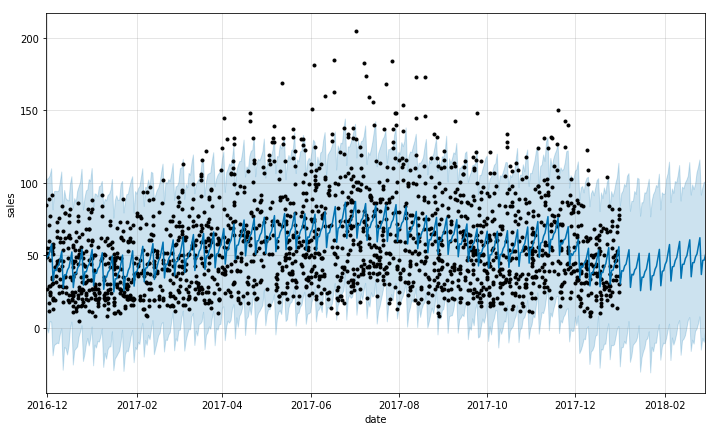
display(predict_fig)
黒い点が実測値、青い線が予測値になります。
また、薄い青の範囲が95%の信頼区間を表しています。
このグラフから良いモデルなのかを判断することは難しいので、よく使われるモデルの指標を算出してみたいと思います。
今回利用する指標として以下の3つを算出したいと思います。
平均二乗誤差 (MSE: Mean Squared Error)
各データにおいて実測値と予測値の誤差を二乗し、平均をとったもの
二乗平均平方根誤差 (RMSE: Root Mean Squared Error)
MSE の平方根をとったもの。MAEに比べて大きな誤差を厳しく評価する特徴がある。
平均絶対誤差 (MAE: Mean Absolute Error)
誤差の絶対値を取り、平均をとったもの。
RMSE に比べて外れ値の影響を受けにくいと言われる。
それぞれ0に近いほど誤差が小さく、精度が高いことがわかります。
import pandas as pd
from sklearn.metrics import mean_squared_error, mean_absolute_error
from math import sqrt
from datetime import date
# 比較のために過去の実績と予測を取得
predicted_pd = forecast_pd[ pd.to_datetime(forecast_pd['ds']).dt.date < date(2018, 1, 1) ]['yhat']
actuals_pd = history_pd[ pd.to_datetime(history_pd['ds']).dt.date < date(2018, 1, 1) ]['y'].sample(len(predicted_pd))
# 制度指標の計算
mae = mean_absolute_error(actuals_pd, predicted_pd)
mse = mean_squared_error(actuals_pd, predicted_pd)
rmse = sqrt(mse)
print('-----------------------------')
print( '\n'.join(['MSE: {0}', 'RMSE: {1}', 'MAE: {2}']).format(mae, mse, rmse) )
算出してみた結果が以下になります。
実際にはここからさらにチューニングしていき、モデルの精度を上げていくことになると思います。
-----------------------------
MSE: 1040.242690489999
RMSE: 32.25279353001844
MAE: 25.966749442943733
まとめ
以上でモデルの作成からモデルの確認までを行いました。
実際は最後に出した値やグラフなどを確認しながらより精度が上がるようにチューニングしていくことになります。
今回はモデルの作成、確認についての理解ということでこちらは省略します。
次回は、モデルの大規模データに対するアプローチやリモデルについてをまとめられたらいいなと思います。