L1は◇、L2は○

機械学習の書籍などでリッジ回帰やラッソ回帰のページを開くとでてくるこの図。
見たことある人も多いだろう。

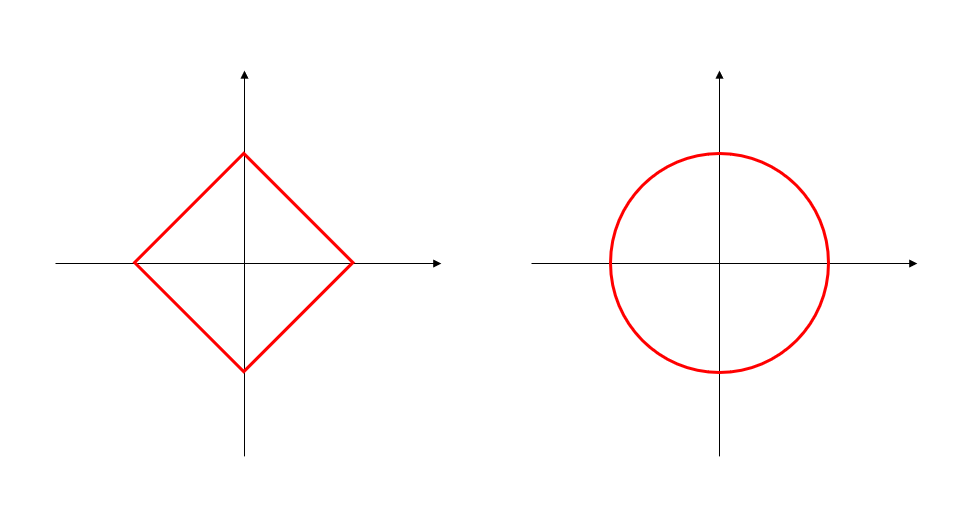
正則化項にL2ノルムを使うのがリッジ回帰、L1ノルムを使うのがラッソ回帰。
過学習を防いだり変数選択ができたりするあれだ。

じゃあL3は...?

詳しい人からしたら「そんなの当たり前だよ」と言われそうだが、
私と同じように機械学習から入った人間からしたらL1、L2しか聞いたことがない、
という人もいるかもしれない（いなかったらごめん）。

L3がそもそもあるのか、あったらどんな形なのか、それを調査したのが本記事である。

もう結論なのだが、一般化するとLpノルムと呼ぶらしい。
つまりp=3の場合がL3ノルムとなる。

Lpノルムの式はこちら。

$ \sqrt[p]{\sum_{i=1}^{n}|x_i|^p}$

L3ノルムを探して真っ先にたどりついた記事がこれ。
【機械学習】LPノルムってなんだっけ？
pの値をいろいろ変えて描画していて、なにより美しい。

Githubに描画のコードも置いてくださっていたので、
こちらを利用して描いたL3ノルムの形がこちら。

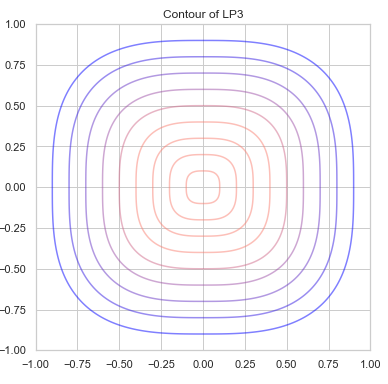
なるほど、角が丸い四角という感じか...!
そしてp=∞のときに完全な正方形になるらしい。

L3ノルムを調べていて学んだことがもうひとつある。
それはL1ノルムの形状はマンハッタン距離であるということ。
碁盤目状に進むやつね。

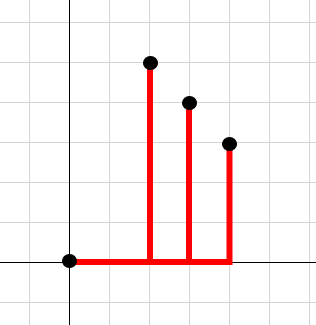
式を見ると確かにそうじゃん！となって少し理解した気になった。

ちなみに
L2ノルムの形状はユークリッド距離
L∞ノルムの形状はチェビチェフ距離ですね。