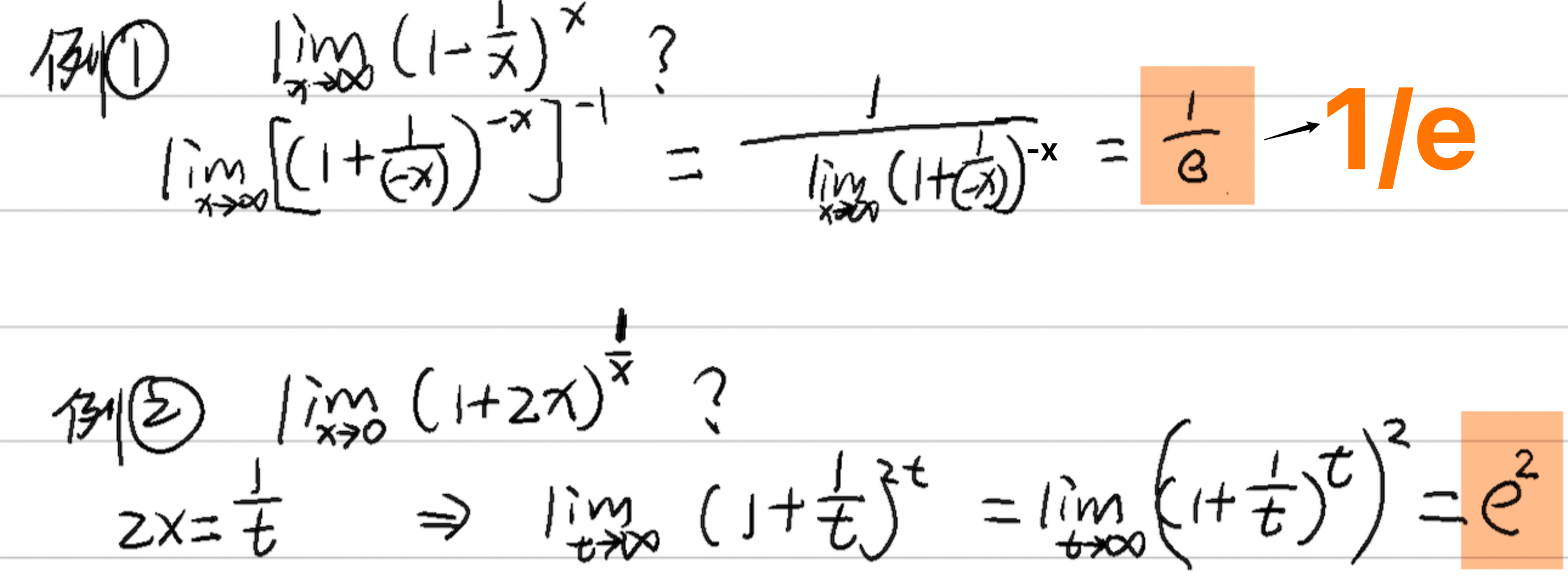本記事は数学講座2.14単調有界数列必ず極限を持つを勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
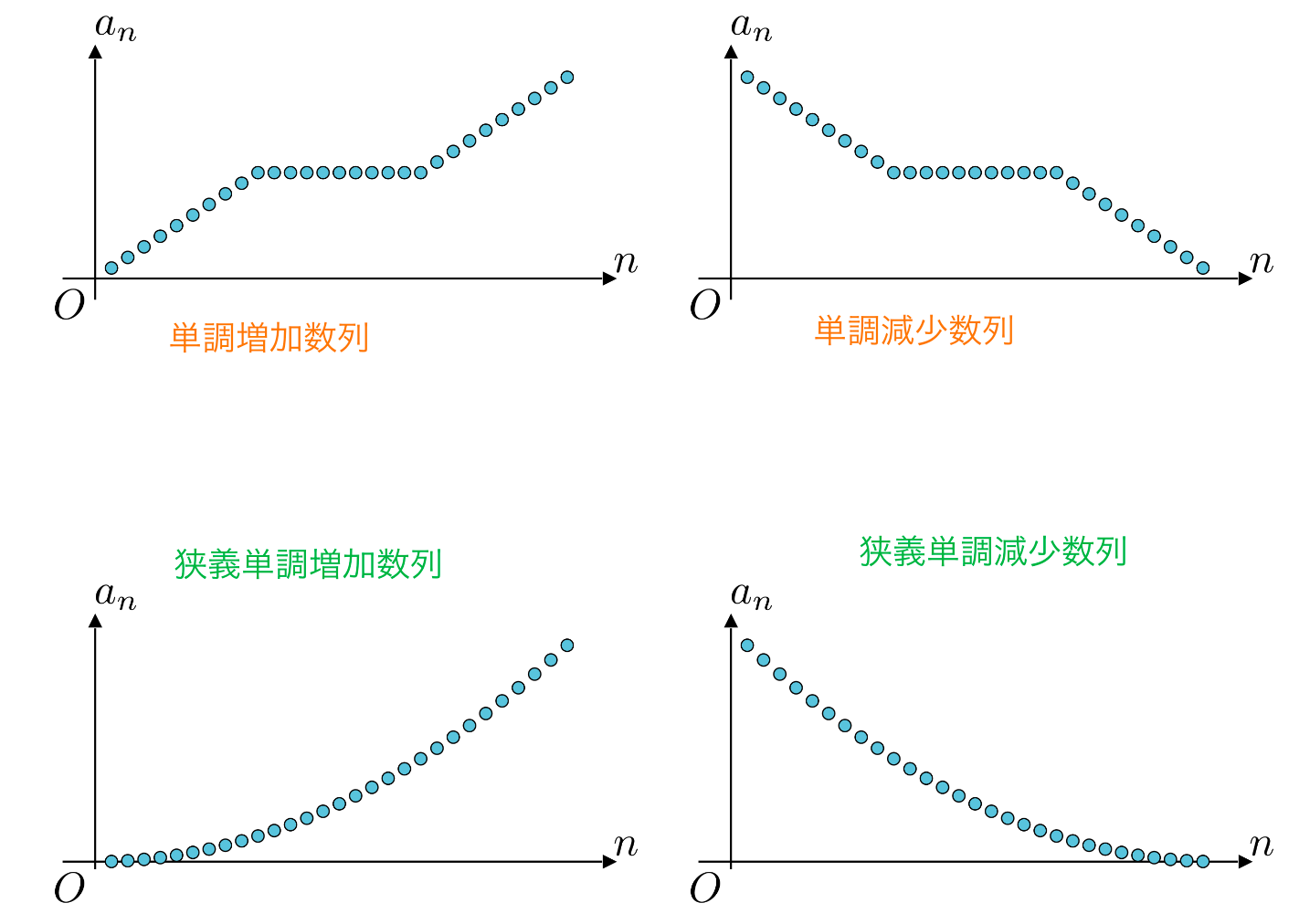
単調な数列と関数
概念：
- 狭義(きょうぎ)単調数列（関数）
- 単調数列（関数）
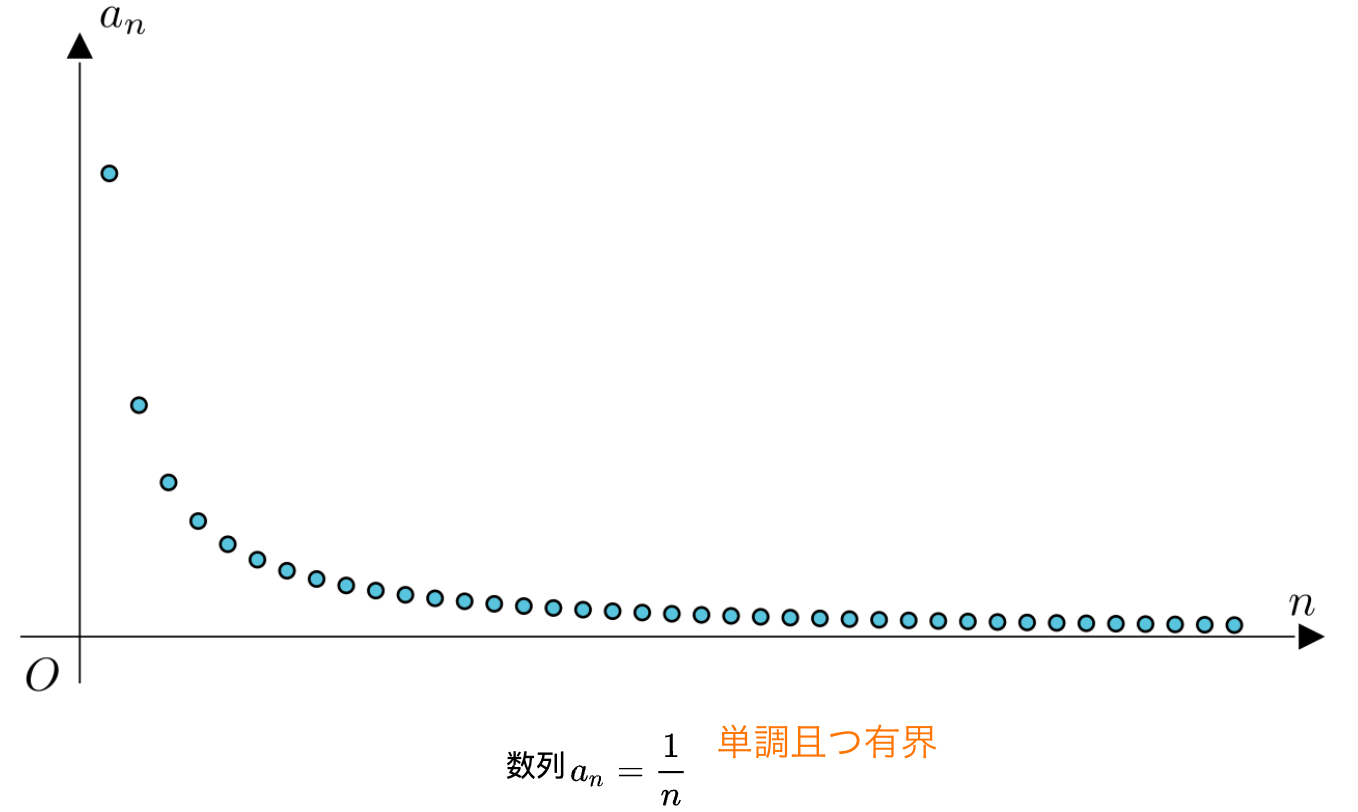
単調有界原則
数列が単調、且つ有界であれば、この数列には必ず極限があり、収束します。
オイラー数 e
定理：
$\displaystyle{a_n}={\left(1+\frac{1}{n}\right)^n}$の極限が存在します、その極限が$e$で表します：
\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n=e
$e$がオイラー数 （Euler's number）、或は自然対数 （Base of the natural logarithms）、無理数です.
$e=2.718\ 281\ 828\ 459\ 045\cdots$
オイラー数 e の例題
