本記事は数学講座4.4 行列関数の性質を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
行列関数の性質
行列の乗法の演算規則のと同じで、行列関数も以下の性質があります。
\begin{array}{c|c}
\hline
\\
\quad 交換律\quad&\quad 必ずしも成立しない\quad\\
\quad スカラー倍交換律\quad&\quad \lambda(AB)=(\lambda A)B=A(\lambda B)（\lambdaが定数）\quad\\
\quad 結合律\quad&\quad (AB)C=A(BC)\quad\\
\quad 配分律\quad&\quad A(B+C)=AB+AC\quad\\
\\
\hline
\end{array}
交換律
行列関数$A,B$の乗法は、関数の複合を考えたらよいです。
AB=A\circ B
$A\circ B$が関数の複合の記号です。例えば、$y=f(x), y=g(x)$の複合が：
f\Big(g(x)\Big)=(f\circ g)(x)
関数の複合は交換できないので、行列関数の交換もできないです。
f(x)=x^2, g(x)=x-2
\\
複合をすると：
\\
f\Big(g(x)\Big)=(f\circ g)(x)=(x-2)^2
\\
≠
\\
g\Big(f(x)\Big)=(g\circ f)(x)=(x^2)-2
行列関数の複合
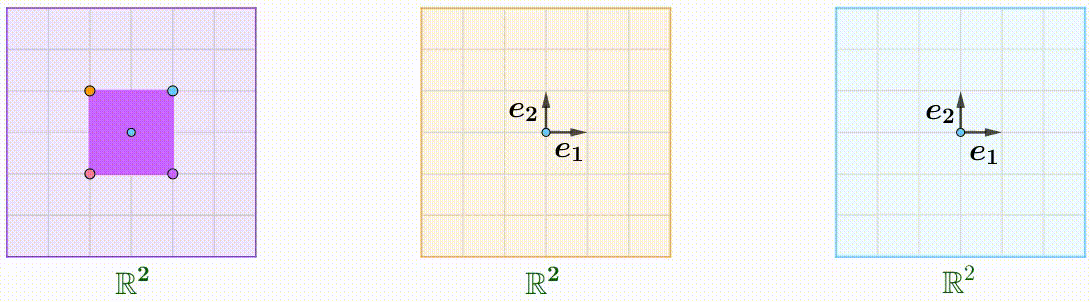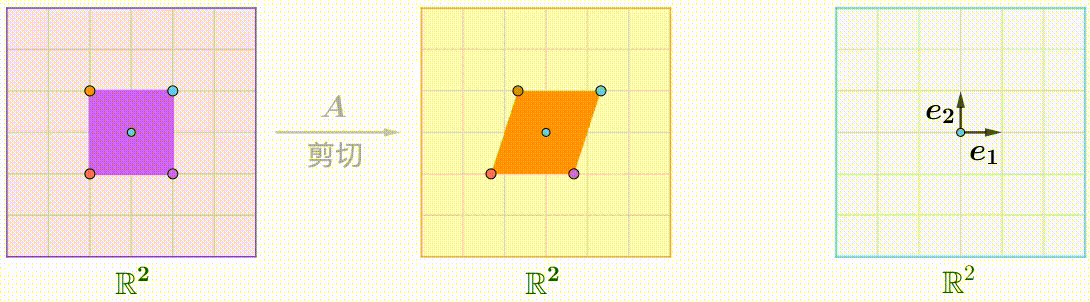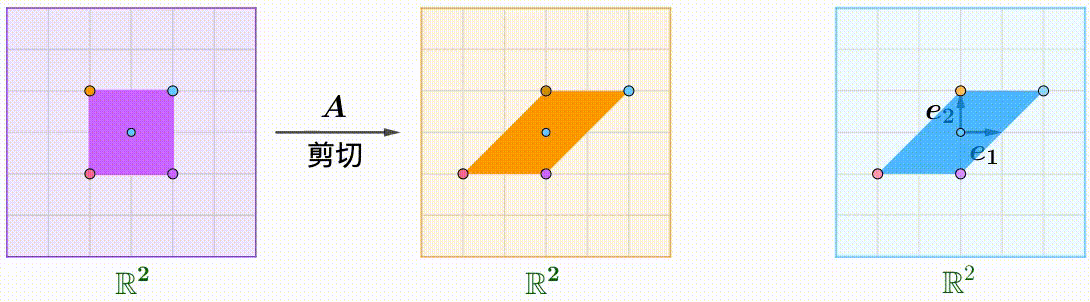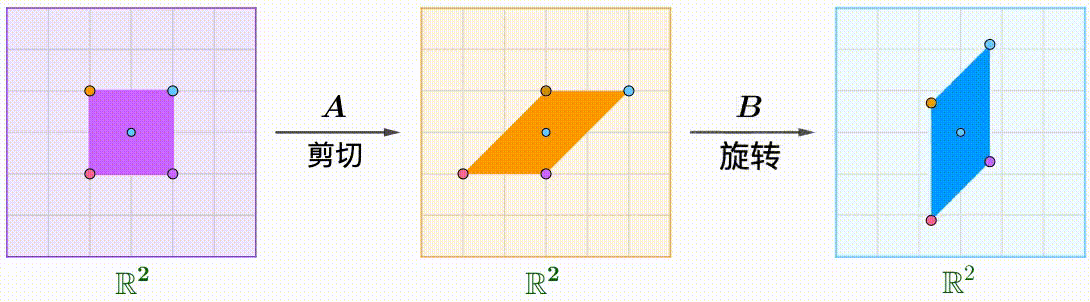
例えば、$A$のShear行列、$B$の回転行列：
A=\begin{pmatrix}1&k\\0&1\end{pmatrix},\quad B=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}
回転とShearの順番が違うと、結果も異なります$AB\ne BA$。
と
結合律
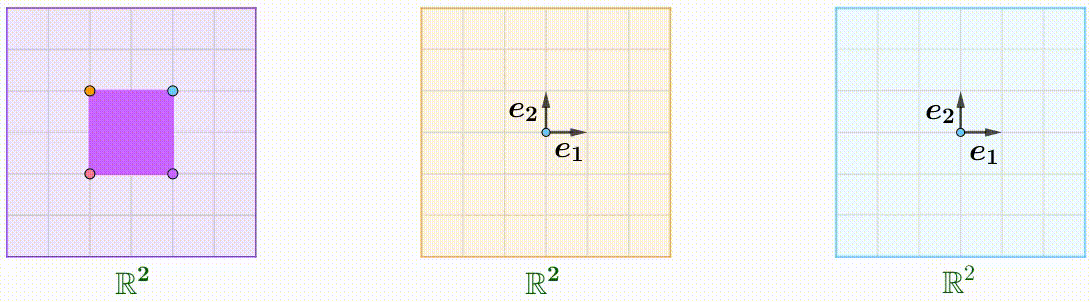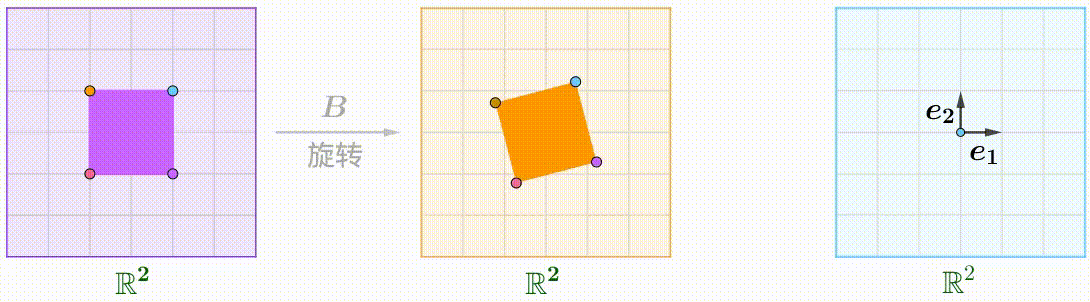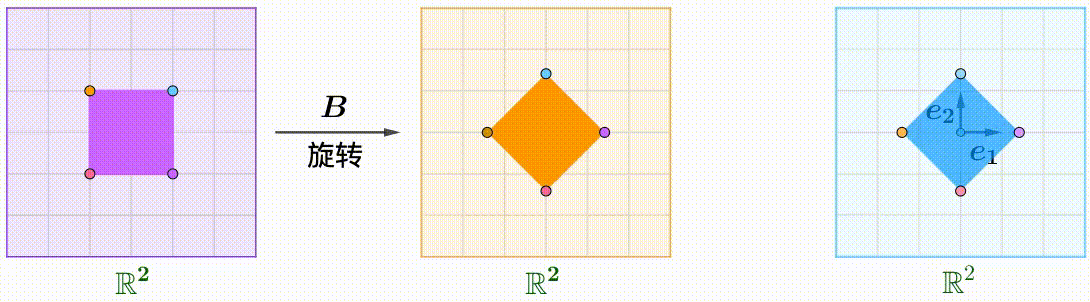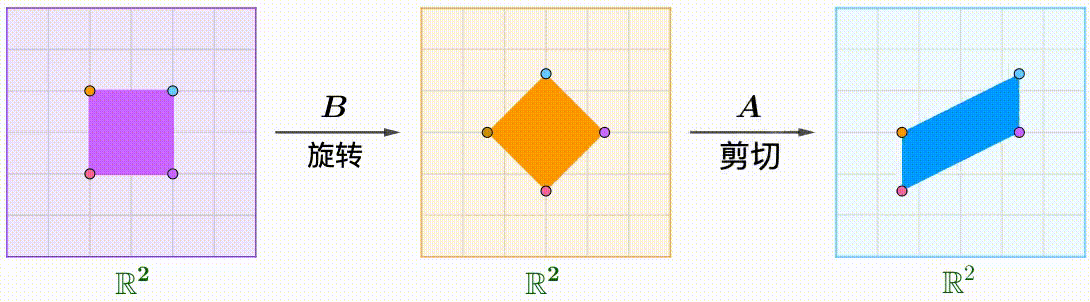
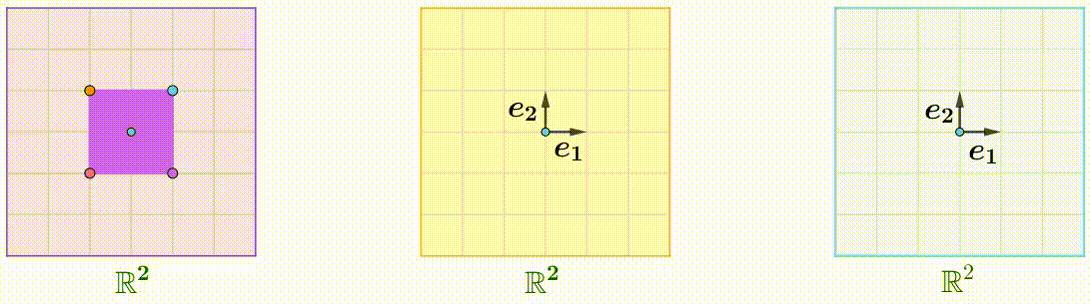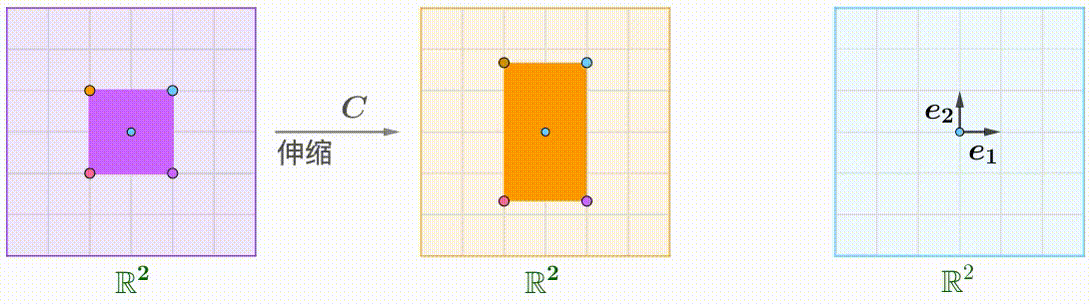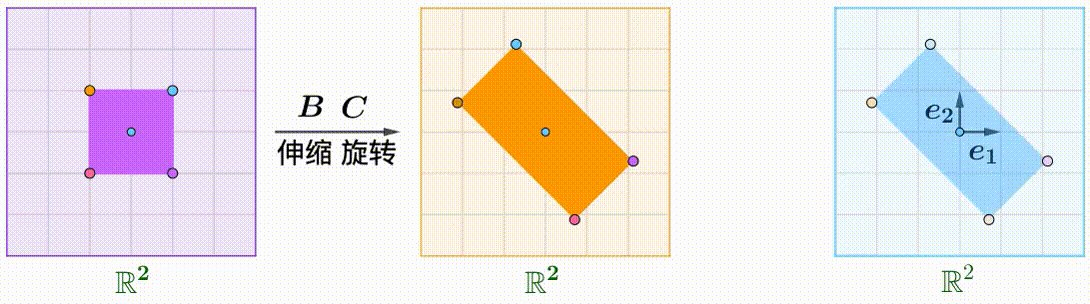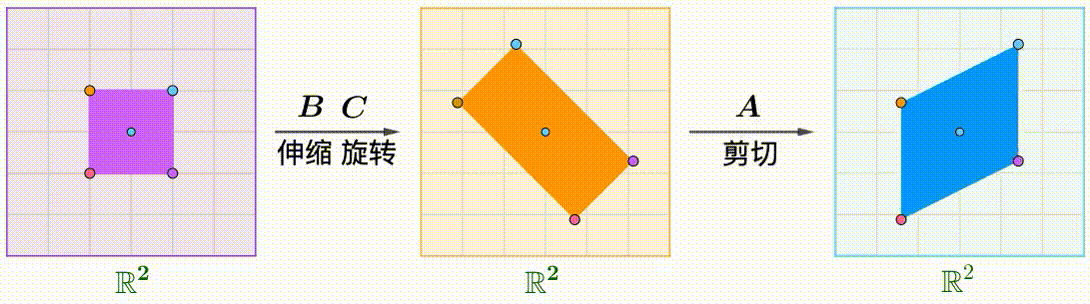
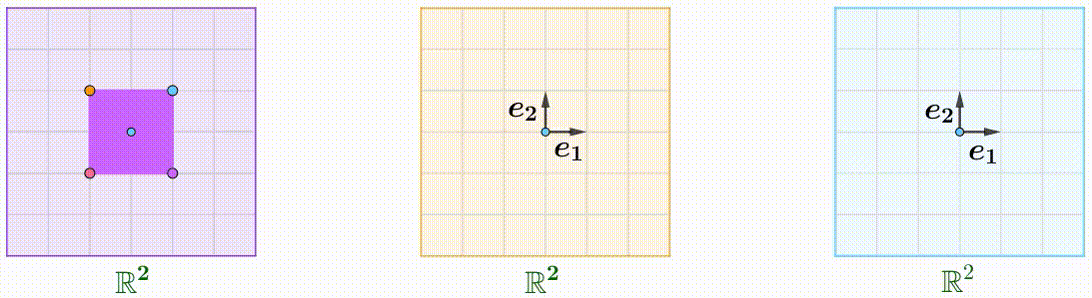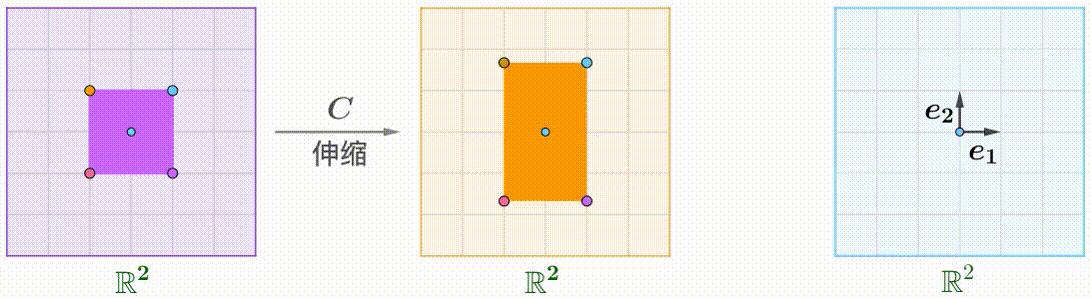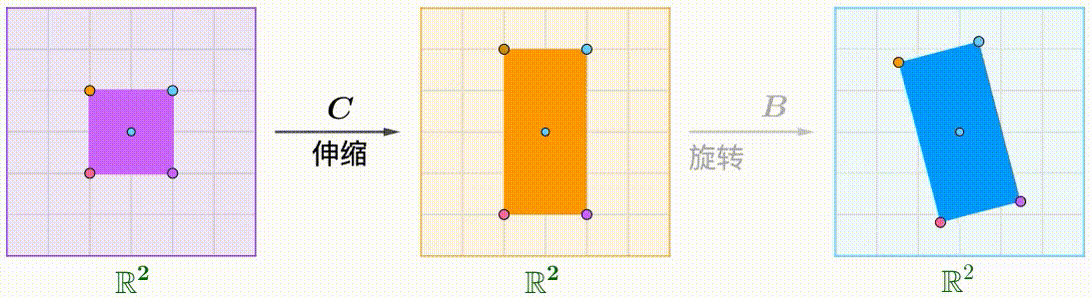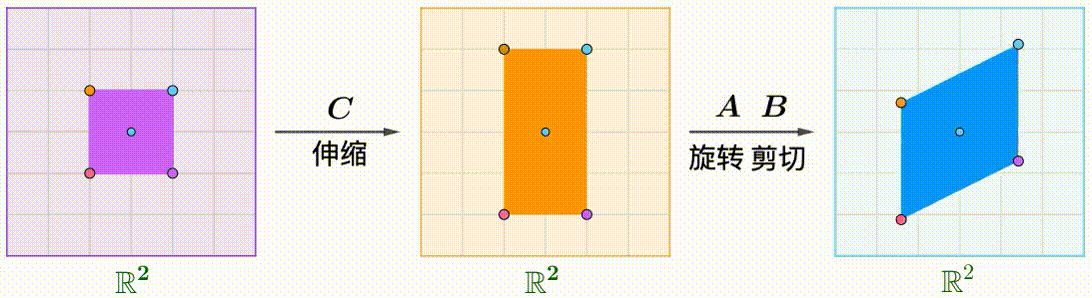
例えば、$A$のShear行列、$B$の回転行列、$C$が拡大縮小行列です：
\boldsymbol{A}=\begin{pmatrix}1&k\\0&1\end{pmatrix},\quad\boldsymbol{B}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix},\quad\boldsymbol{C}=\begin{pmatrix}1&0\\0&2\end{pmatrix}
$A(BC)$: 先に拡大縮小と回転をして、Shear：
$(AB)C$: 先に拡大縮小をして、回転とShear：
$\boldsymbol{A}(\boldsymbol{B}\boldsymbol{C})=(\boldsymbol{A}\boldsymbol{B})\boldsymbol{C}$が分かります。
補足
$A,B$が$n$次元の行列で、$(A-B)(A+B)$の計算は：
\begin{aligned}
(A-B)(A+B)
&=A(A+B)-B(A+B)&&配分律\\
&=A^2+AB-BA-B^2&&配分律\\
\end{aligned}
$AB$と$BA$が必ずしも等しいではないです。