本記事は数学講座6.1 解の存在性を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
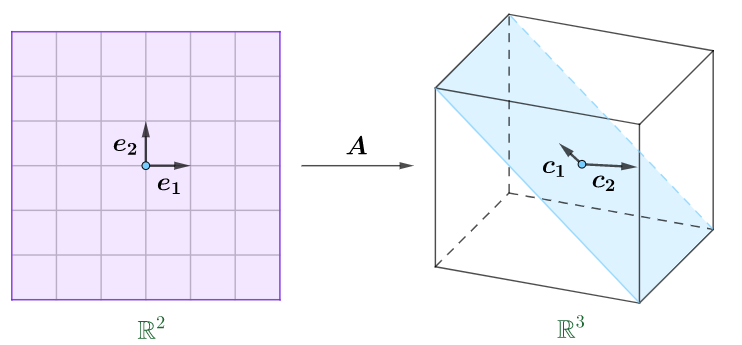
解の存在性に関して、データサイエンスのための線形代数 第22回 行列関数の全単射で解説した通り、行列$A$が単射、全射、全単射かに関わっています。
\begin{array}{c|c|c|c}
\hline
\quad行列関数\quad&\quad 単射の必要十分条件 \quad&\quad 全射の必要十分条件 \quad&\quad 全単射の必要十分条件 \quad\\\hline\\
\quad \begin{aligned}A\boldsymbol{x}=\boldsymbol{y}\ \ \\\boldsymbol{x}^\mathrm{T}A=\boldsymbol{y}^\mathrm{T}\end{aligned} \quad&\quad \begin{aligned}列フルランク\\行フルランク\end{aligned} \quad&\quad \begin{aligned}行フルランク\\列フルランク\end{aligned} \quad&\quad フルランク\quad\\
\\
\hline
\end{array}
補足：
- 単射：定義域＝値域、唯一な解あるか
- 全射：到達域＝値域、解存在か(指定の値が値域にあるのか)
- 全単射：定義域＝値域＝到達域、解ある且つ唯一な解
幾何観点からの線形方程式
二つ未知数の線形方程式
以下のように二つ未知数の線形方程式：
\begin{cases}
a_{11}x_1+a_{12}x_2=b_{1}\\
a_{21}x_1+a_{22}x_2=b_{2}\\
a_{31}x_1+a_{32}x_2=b_{3}
\end{cases}
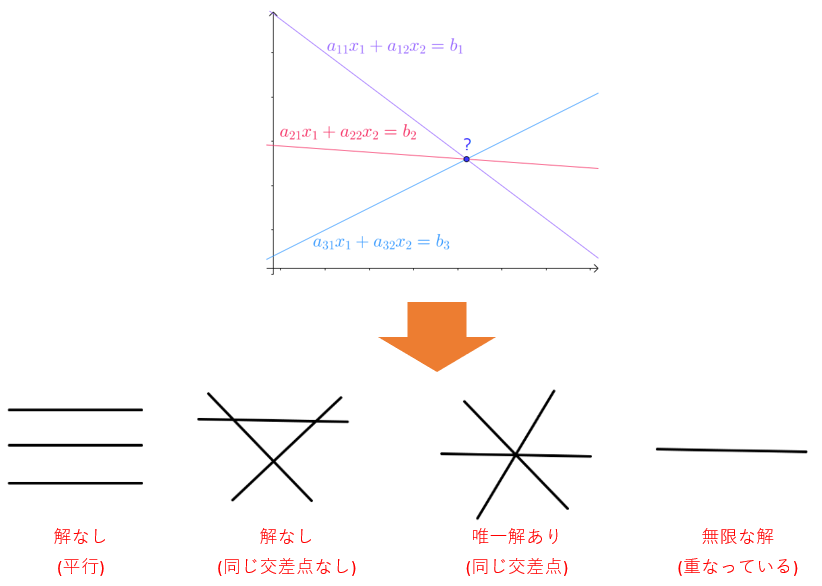
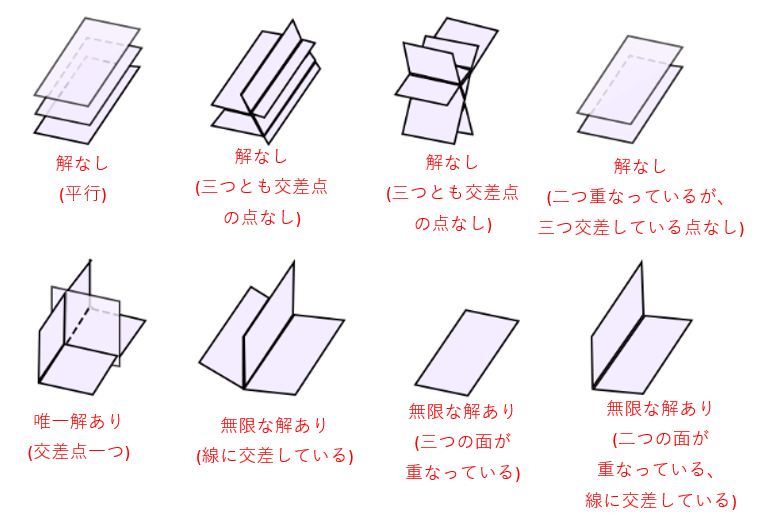
幾何的に見れば、これが三本の線の交差点があるのかを解きます。
三つの未知数の線形方程式
以下のように三つ未知数の線形方程式：
\begin{cases}
a_{11}x_1+a_{12}x_2+a_{13}x_3=b_{1}\\
a_{21}x_1+a_{22}x_2+a_{23}x_3=b_{2}\\
a_{31}x_1+a_{32}x_2+a_{33}x_3=b_{3}
\end{cases}
幾何的に見れば、これが三つの面の交差点があるのかを解きます。
行列観点からの線形方程式
以下のような二つ未知数の線形方程式があります。
\begin{cases}
a_{11}x_1+a_{12}x_2=b_{1}\\
a_{21}x_1+a_{22}x_2=b_{2}\\
a_{31}x_1+a_{32}x_2=b_{3}
\end{cases}
行列の乗法式へ変更すると：
\underbrace{\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32}\end{pmatrix}}_{A}\underbrace{\begin{pmatrix}x_1\\x_2\end{pmatrix}}_{\boldsymbol{x_{}}}=\underbrace{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}_{\boldsymbol{b_{}}}\implies A\boldsymbol{x_{}}=\boldsymbol{b_{}}
これが行列関数の$Ax=y$、$y=b$の時の$x$の解の状況です。
更に一般的な線形方程式系になると：
\begin{cases}
a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_{1}\\
a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_{2}\\
\qquad\qquad\quad\vdots\qquad\qquad\quad\vdots\\
a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n=b_{m}
\end{cases}
\implies
\underbrace{A}_{m\times n}\quad\underbrace{\boldsymbol{x_{}}}_{n\times 1}\quad=\quad\underbrace{\boldsymbol{b_{}}}_{m\times 1}
これも行列関数の$Ax=y$、$y=b$の時の$x$の解の状況です。
上記のように、線形方程式が行列関数です。これから行列関数の知識で、線形方程式を解くようにします。まず
以下の三つの問題を見ていきます。
- 解の存在性：$Ax=y$で、$y=b$の時に、$x$が存在するか
- 解の件数：$Ax=y$で、$y=b$の時に、$x$が何件存在するか
- 解の集合：$Ax=y$で、$y=b$の時に、具体的に、どれら$x$ なのか
この記事では、まず解の存在性を確認します。
解が存在するか $=$ $b$の値が値域に存在しているか、存在していれば、定義域に相応な$x$があるので、解があります。
解と行列関数の値域
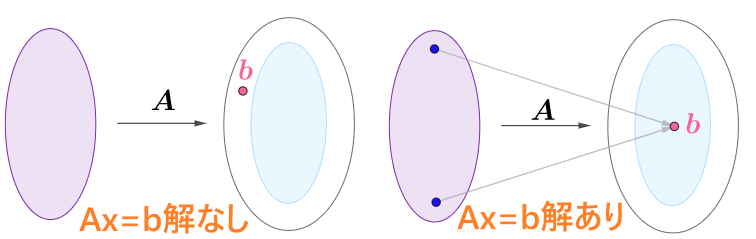
行列関数型の線形方程式$Ax=y$に対して、$b$が行列関数$AX=y$の値域内に存在しているか を判断できれば、解があるかがわかります。
\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}\ \ \begin{cases}\text{解なし：}&\boldsymbol{b}\ \text{が}\ \boldsymbol{A}\boldsymbol{x}=\boldsymbol{y}\ \text{の値域内ではない}\\\text{解あり解：}&\boldsymbol{b}\ \text{が}\ \boldsymbol{A}\boldsymbol{x}=\boldsymbol{y}\ \text{の値域内}\end{cases}
例１(解なし→線形独立)：
以下の線形方程式には、$x$の解があるか？
\begin{cases}x_1-x_2=1\\x_1-x_2=2\end{cases}
まず、線形方程式から行列関数へ変換します。
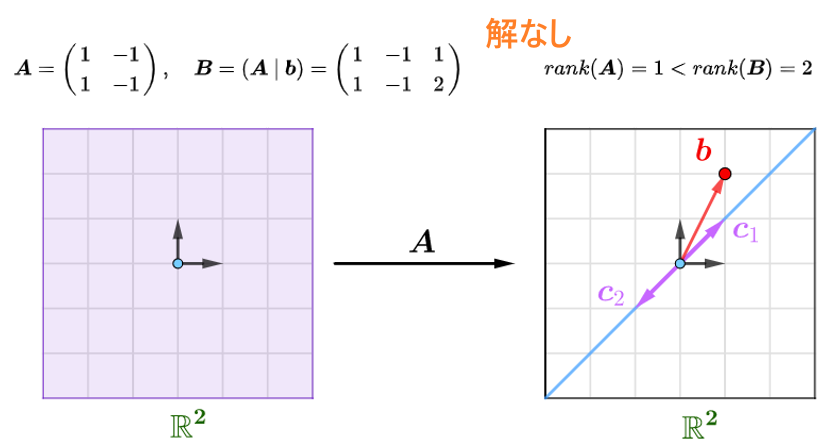
\begin{cases}x_1-x_2=1\\x_1-x_2=2\end{cases}\implies\underbrace{\begin{pmatrix}1&-1\\1&-1\end{pmatrix}}_{\boldsymbol{A}}\underbrace{\begin{pmatrix}x_1\\x_2\end{pmatrix}}_{\boldsymbol{x}}=\underbrace{\begin{pmatrix}1\\2\end{pmatrix}}_{\boldsymbol{b}}
$A$の列ベクトルが：
\boldsymbol{c_1}=\begin{pmatrix}1\\1\end{pmatrix},\quad\boldsymbol{c_2}=\begin{pmatrix}-1\\-1\end{pmatrix}
{$c1,c2$}の列ベクトル組の張る空間が行列関数$Ax=y$の値域です。{$c1,c2$}が線形従属で、平面での線になります。
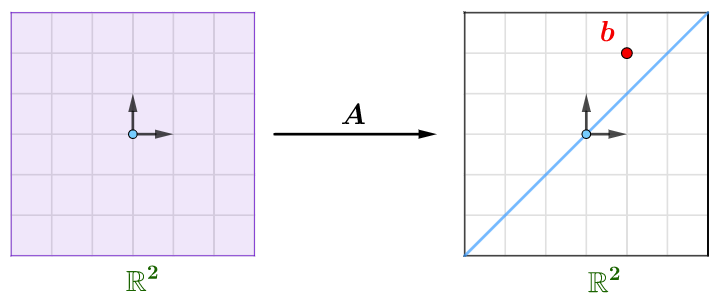
$b$が線に存在していないので、該当線形方程式には解なしです。
例２(解あり→線形従属)：
以下の線形方程式には、$x$の解があるか？
\begin{cases}-x_1+2x_2=0\\\qquad\quad2x_2=2\\\ \ \ x_1-2x_2=0\end{cases}
まず、線形方程式から行列関数へ変換します。
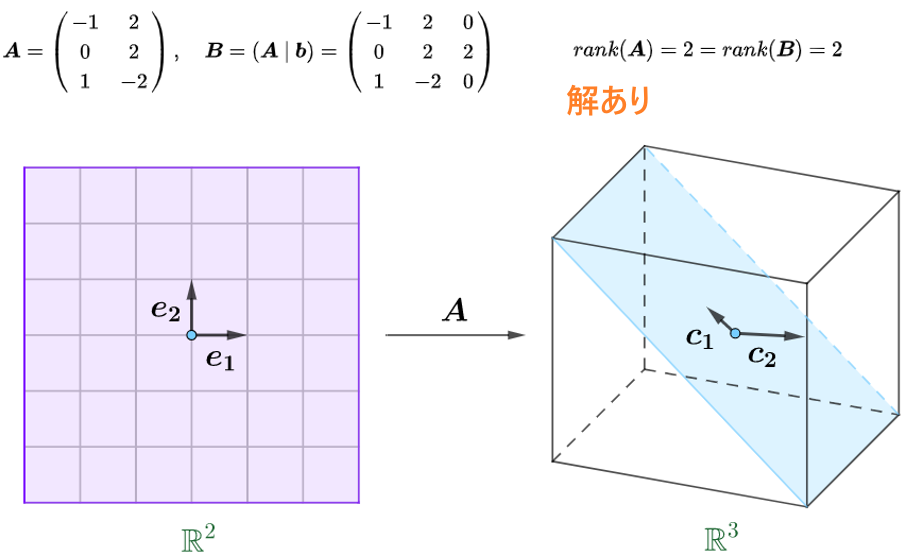
\begin{cases}-x_1+2x_2=0\\\qquad\quad2x_2=2\\\ \ \ x_1-2x_2=0\end{cases}\implies\underbrace{\begin{pmatrix}-1&2\\0&2\\1&-2\end{pmatrix}}_{\boldsymbol{A}}\underbrace{\begin{pmatrix}x_1\\x_2\end{pmatrix}}_{\boldsymbol{x}}=\underbrace{\begin{pmatrix}0\\2\\0\end{pmatrix}}_{\boldsymbol{b}}
$A$の列ベクトルが：
\boldsymbol{c_1}=\begin{pmatrix}-1\\0\\1\end{pmatrix},\quad\boldsymbol{c_2}=\begin{pmatrix}2\\2\\-2\end{pmatrix}
値域が$\mathbb{R}^3$の水色の平面です。
$b$が列ベクトル組{$c1,c2$}の線形結合なので、$b$が$A$の列空間内 $colsp(\boldsymbol{A})$です。
\boldsymbol{b}=2\boldsymbol{c_1}+\boldsymbol{c_2}\in colsp(\boldsymbol{A})
$b$が行列関数$Ax=y$の値域内ですので、解があります。
解の存在性
定理（解の存在性）：
線形方程式$\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$について、その拡大行列を$\boldsymbol{B}=(\boldsymbol{A}\ |\ \boldsymbol{b_{}})$とするとき、以下の条件が成り立つ:
- 解なしの場合、$rank(\boldsymbol{A}) < rank(\boldsymbol{B})$である。
- 解ありの場合、$rank(\boldsymbol{A})=rank(\boldsymbol{B})$である。
$rank(\boldsymbol{A})=rank(\boldsymbol{B})$であれば、$b$が$Ax$の線形結合なので、$b$が$Ax$の張る空間(値域)にあります。
上記の例１と例２：
-
解なし：$b$が$A$のベクトル空間外なので、ランクが増えます
-
解あり：$b$が$A$のベクトル空間内なので、ランクが変わらない
行フルランクの行列は必ず解あり
行列$A$：$A$が行フルランク $➡$ $Ax=b$解あり
$A$が行フルランクの時に、$Ax=y$が全射、到達域での$b$も値域に存在するので、$Ax=b$は必ず解あり。
練習
- 以下の線形方程式に解ありか？
\begin{cases}x+y+z=2\\2x+y-z=3\\-2x+y-z=1\end{cases}
- 以下の線形方程式に解ありか？
\begin{cases}x+y+z=0\\-2x-y+z=0\\x+y+z=1\end{cases}
