本記事は数学講座2.6無限小を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
無限小の定義
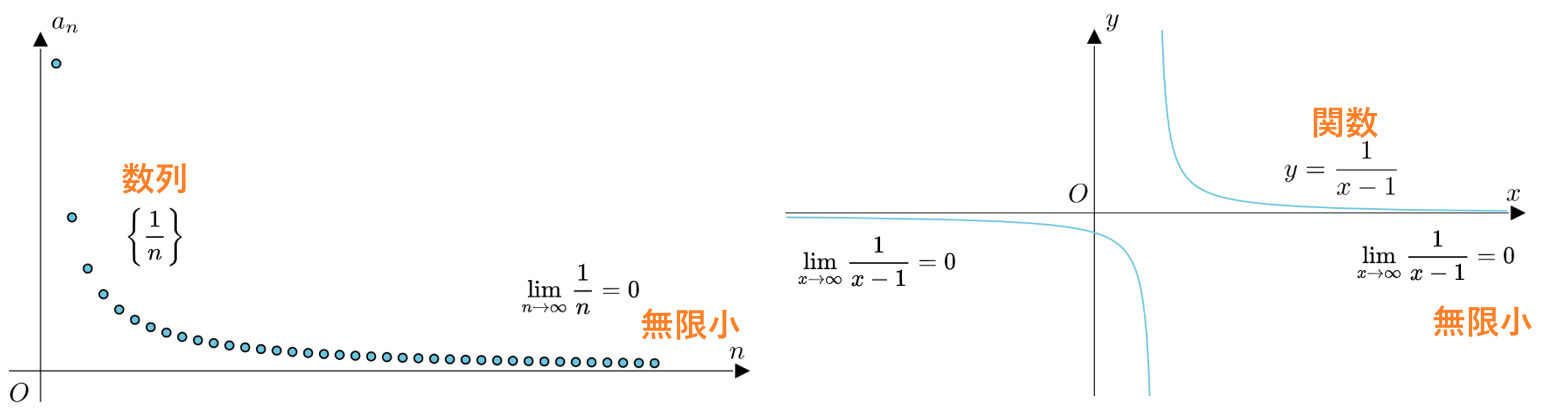
数列{$a_n$}にとって、$\displaystyle\lim_{n\to\infty}a_n=0$があれば,数列{$a_n$}が$n\to\infty$のときの無限小(Infinitesimal) です。
同じで、関数$f(x)$にとって、$\lim f(x)=0$があれば、関数$f(x)$が$x\to x_0,x\to\infty$などの時の無限小(Infinitesimal) です。
例えば、
極限と無限小
極限$\lim f(x)=L$が存在の充分必要な条件:
f(x)=L+\alpha\iff \lim f(x)=L
$\alpha$が無限小、即ち、$\lim\alpha=0$です。
練習
参照