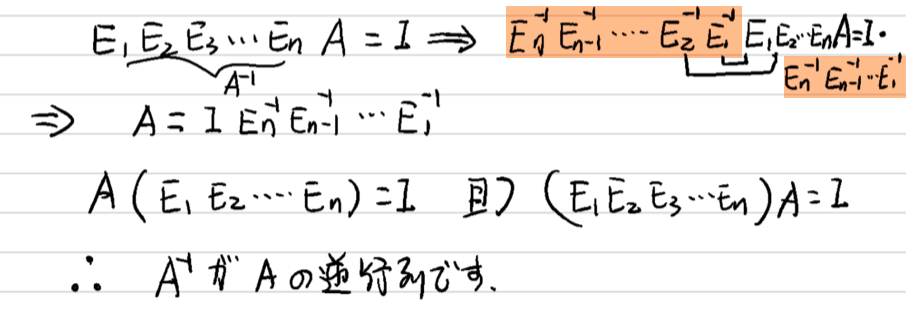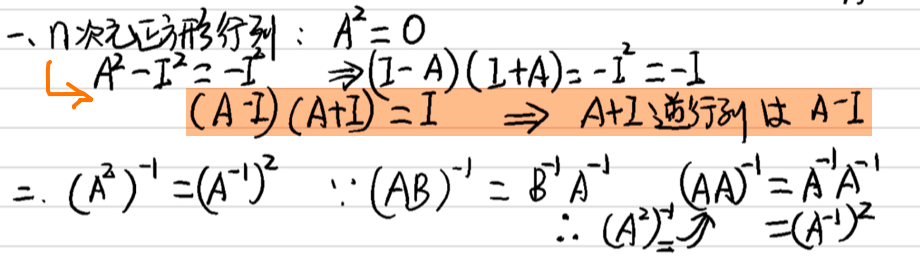本記事は数学講座5.7 逆行列を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
 逆行列の演算規則
逆行列の演算規則
- $A$は逆行列があれば、$A^{-1}$も逆行列あり:$(\boldsymbol{A}^{-1})^{-1}=\boldsymbol{A}$
- $A$は逆行列があり、実数 $\lambda\ne 0$、$\lambda\boldsymbol{A}$も逆行列あり:$(\lambda\boldsymbol{A})^{-1}=\frac{1}{\lambda}\boldsymbol{A}^{-1}$
- $A$と$B$とも逆行列あり且つ次元数が同じな正方形行列、$\boldsymbol{A}\boldsymbol{B}$も逆行列あり:$(\boldsymbol{A}\boldsymbol{B})^{-1}=\boldsymbol{B}^{-1}\boldsymbol{A}^{-1}$
- $A$は逆行列があれば、$A^{-T}$も逆行列あり: $ (\boldsymbol{A}^\mathrm{T})^{-1}=(\boldsymbol{A}^{-1})^\mathrm{T}$
全単射と逆関数
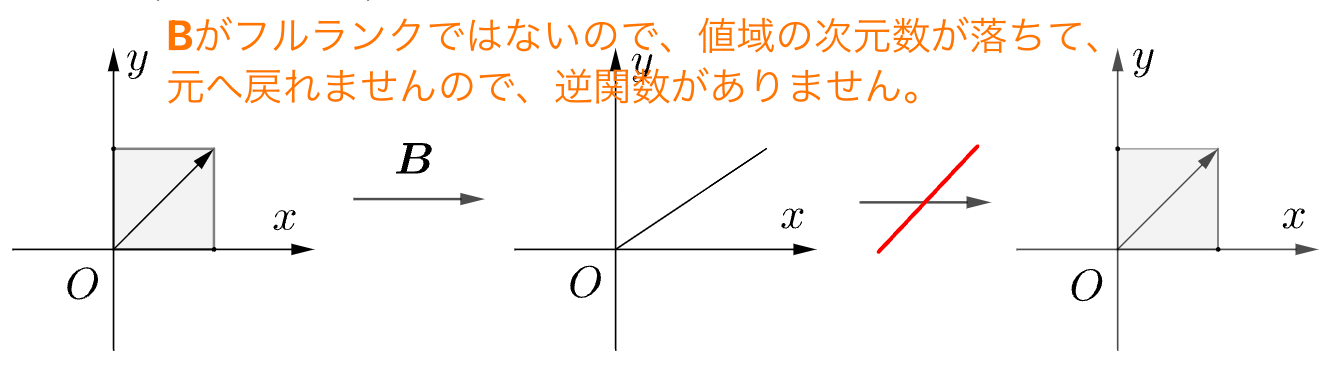
単射あるいは全射だけでは、逆関数の条件が満たされません。


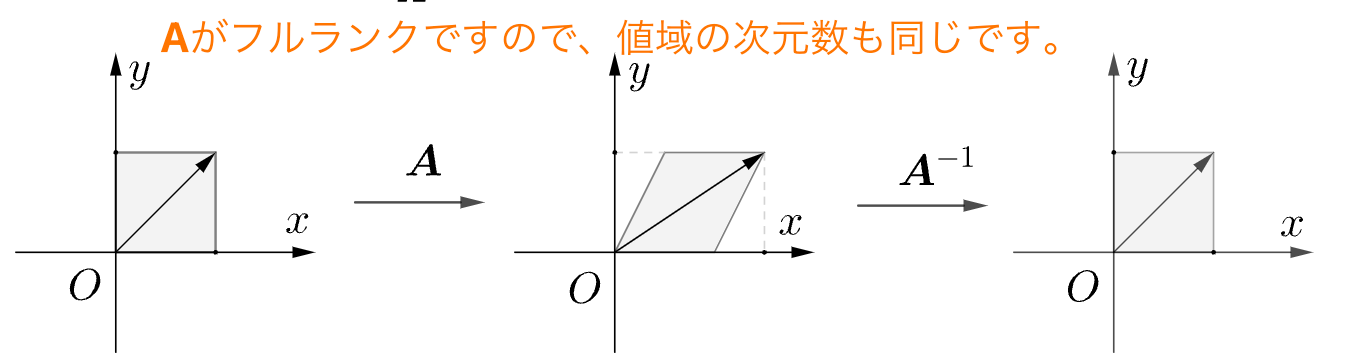
全単射のみの場合には、逆関数があります。

逆行列の存在性
行列 $\boldsymbol{A}$ がフルランク行列であるとき、対応する行列関数は全単射となり、このとき行列 $\boldsymbol{A}$ は逆行列が存在し、$\boldsymbol{A}$ は可逆であると言います。逆行列は $\boldsymbol{A}^{-1}$ で表され、$\boldsymbol{A}$ の逆行列と呼ばれます。
逆行列の定義
二つ$n$次元の正方形行列$A,C$があり、$A,C$のドット積が$n$次元の単位行列$I$:
$AC=I$ 且つ $CA=I$
があれば、$C$が$A$の逆行列です。即ち$A^{-1}=C$、且つ$A^{-1}$が唯一のものです。
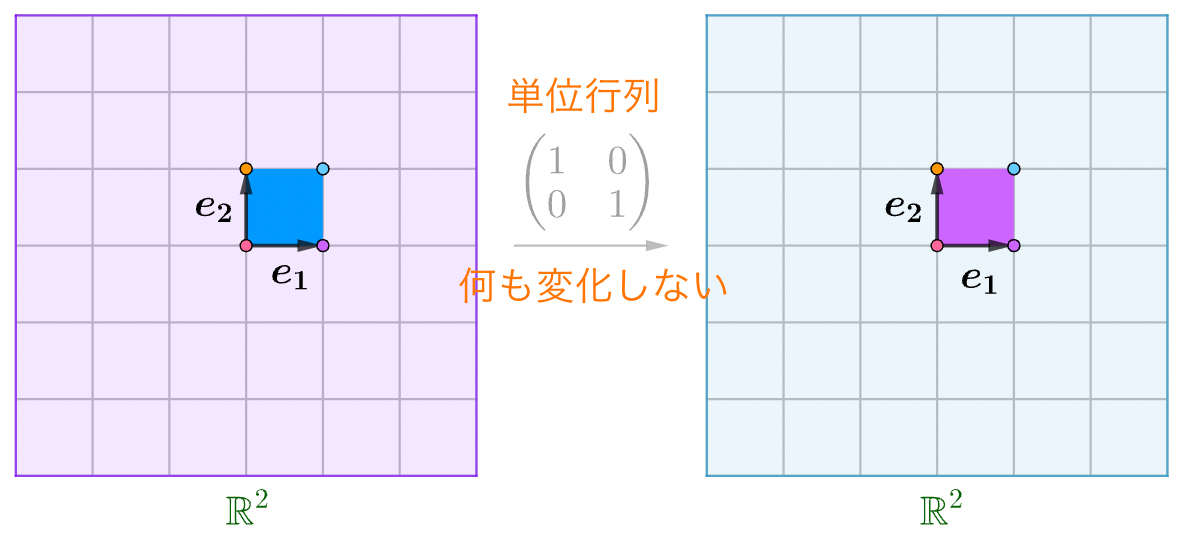
単位行列
$Ax=y$、$A$が単位行列であれば、前後の変化がありません。
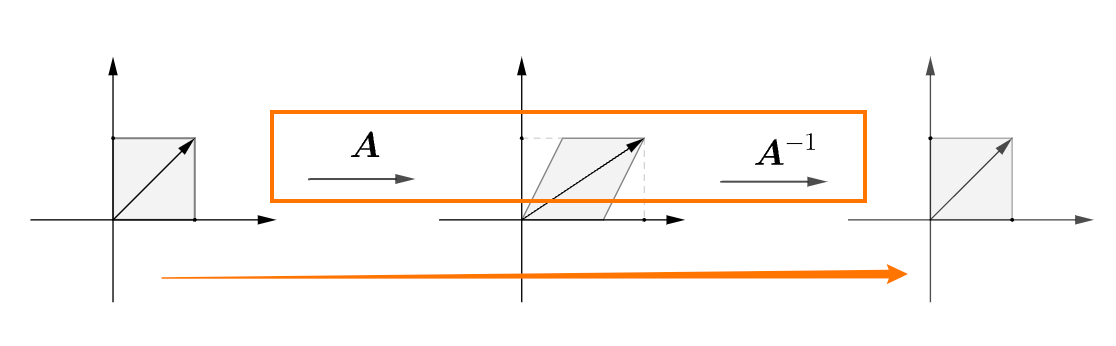
先に行列$A$をかけて、再度逆行列$A^{-1}$をかければ、単位行列と同じように、前後の変化がありません。
だから、単位行列と$AA^{-1}$の合成の効果が同じです。
$I=AA^{-1}=A^{-1}A$
基本行列を用いた逆行列の求め方
一連の基本行列$\boldsymbol{E_i}$を通して、行列$\boldsymbol{A}$を変換して、単位行列$\boldsymbol{I}$
\underbrace{\boldsymbol{E}_1\boldsymbol{E}_2...\boldsymbol{E}_n}_{\boldsymbol{A}^{-1}}\boldsymbol{A}=\boldsymbol{I}
逆行列の存在条件:$A$がフルランク、且つ$AA^{-1}$=Iが成立している。
基本行列を用いた逆行列の例題
例えば、以下行列の逆行列は:
\boldsymbol{A}=\begin{pmatrix}2&3\\1&2\end{pmatrix}

ガウス・ジョルダン法を用いた逆行列の求め方
以下の二つステップで、行列の逆行列$AA^{-1}=1$を解くことができます:
A\xrightarrow{\quad E_1,E_2,...,E_n\quad }I
次は、それらの積:
A^{-1}=E_1E_2...E_n
ただし、2ステップが煩雑ですので、まとめて計算することが可能です。
( A|I )\xrightarrow{\quad E_1,E_2,...,E_n\quad }( I|A^{-1} )
例題

まだ十分理解できていないと思うんですが、こちらのメリットはどこだろう?人的に計算すれば、そんなメリットが感じていません。最後の1ステップの計算を分散して、前のステップに混ぜっただけですね。
もしかしたら、これがプログラミングする際に、便利になる技ですかね?
逆行列の演算規則
-
$A$は逆行列があれば、$A^{-1}$も逆行列あり:$(\boldsymbol{A}^{-1})^{-1}=\boldsymbol{A}$
説明:逆行列の定義によれば、$AC=I且つCA=I$ですので、$C$が$A$の逆行列、$A$が$C$も逆行列です、お互いの関係です。
-
$A$は逆行列があり、実数 $\lambda\ne 0$、$\lambda\boldsymbol{A}$も逆行列あり:$(\lambda\boldsymbol{A})^{-1}=\frac{1}{\lambda}\boldsymbol{A}^{-1}$
実際に計算すれば、その積が単位行列ですので、上記のが成立している。
\lambda\boldsymbol{A}\cdot\frac{1}{\lambda}\boldsymbol{A}^{-1}=\frac{1}{\lambda}\boldsymbol{A}^{-1}\cdot\lambda\boldsymbol{A}=\boldsymbol{I}
- $A$と$B$とも逆行列あり且つ次元数が同じな正方形行列、$\boldsymbol{A}\boldsymbol{B}$も逆行列あり:$(\boldsymbol{A}\boldsymbol{B})^{-1}=\boldsymbol{B}^{-1}\boldsymbol{A}^{-1}$
実際に計算すれば、その積が単位行列ですので、上記のが成立している。
(\boldsymbol{A}\boldsymbol{B})(\boldsymbol{B}^{-1}\boldsymbol{A}^{-1})=\boldsymbol{A}(\boldsymbol{B}\boldsymbol{B}^{-1})\boldsymbol{A}^{-1}=\boldsymbol{A}\boldsymbol{I}\boldsymbol{A}^{-1}=\boldsymbol{A}\boldsymbol{A}^{-1}=\boldsymbol{I}
実際に計算すれば、その積が単位行列ですので、上記のが成立している。
- $A$は逆行列があれば、$A^{-T}$も逆行列あり: $ (\boldsymbol{A}^\mathrm{T})^{-1}=(\boldsymbol{A}^{-1})^\mathrm{T}$
転置行列の性質の$(AB)^\mathrm{T}=B^\mathrm{T}A^\mathrm{T}$があるので、代入すれば:
\boldsymbol{A}^\mathrm{T}(\boldsymbol{A}^{-1})^\mathrm{T}=(\boldsymbol{A}^{-1}\boldsymbol{A})^\mathrm{T}=\boldsymbol{I}^\mathrm{T}=\boldsymbol{I}
練習
参考情報