本記事は数学講座5.3 行列関数の値域を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
 [まとめ] ランクの性質
[まとめ] ランクの性質
- ランクの値の範囲
0\le rank(A_{m\times n})\le\min(m,n)
- 転置行列のランク
rank(A)=rank(A^\mathrm{T})
- 合成関数のランク
rank(AB)\leq\min\Big(rank(A),rank(B)\Big)
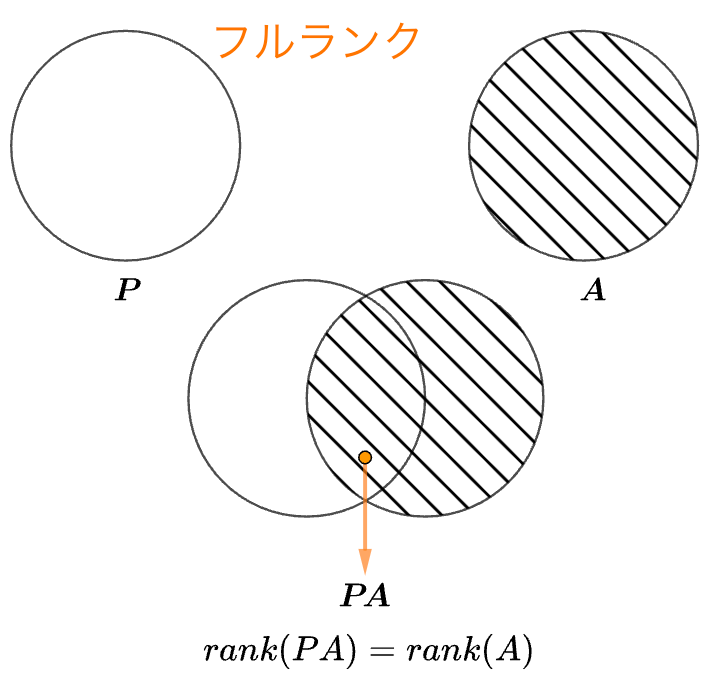
- $P,Q$がフルランクの行列であれば:
rank(PA)=rank(AQ)=rank(PAQ)=rank(A)
- $A,B$が同じ形の行列であれば:
rank(A+B)\le rank(A)+rank(B)
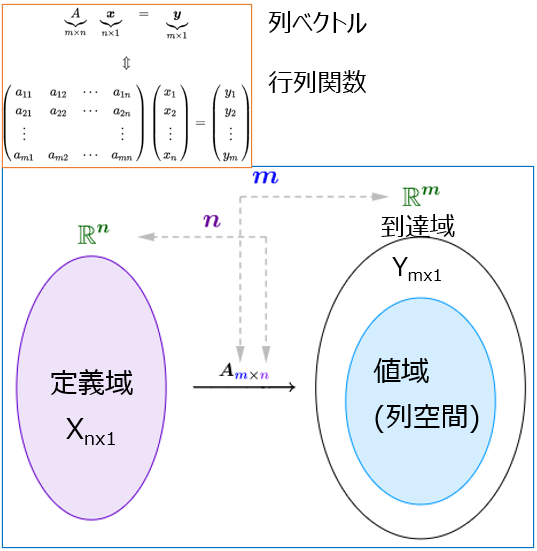
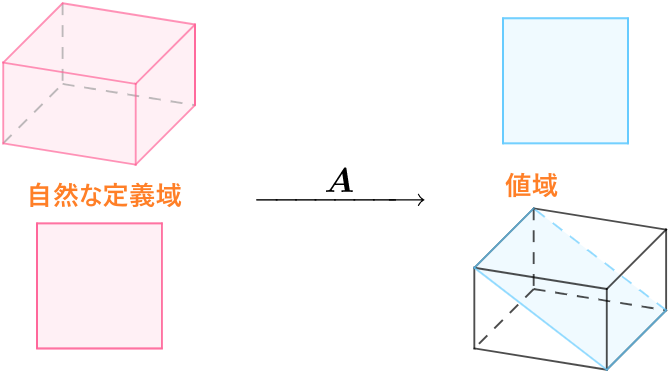
列ベクトル行列関数の値域
自然な定義域で、列ベクトル行列関数$Ax=y$の値域が$A$の列空間です。即ち:$値域=colsp(A)$
例えば、$A$が$m\times n$のぎょうれであり、列ベクトル行列関数$Ax=y$の自然定義域が$R^n$であり、自然定義域での認識なベクトル$x$が$R^n$の自然基底の{$e_1,e_2,e_3...e_n$}で表せます。
\boldsymbol{x}=x_1\boldsymbol{e}_1+x_2\boldsymbol{e}_2+\cdots+x_n\boldsymbol{e}_n,\quad x_{1,2,\cdots,n}\in\mathbb{R}
$A$の列ベクトルが$c_1,c_2,..c_n$: $A=(c_1,c_2,..c_n)$
行列の乗法によれば、列ベクトル行列関数$Ax=y$での$y$が
\boldsymbol{y}=x_1\boldsymbol{c}_1+x_2\boldsymbol{c}_2+\cdots+x_n\boldsymbol{c}_n,\quad x_{1,2,\cdots,n}\in\mathbb{R}
値域$y$が列ベクトル組{$c_1,c_2,..c_n$}の張る空間です。値域が列空間です。
$A$が$m\times n$の行列であれば、自然な定義域での関数$Ax=y$四つ要素が:
\begin{array}{c|c|c|c}
\hline
\quad 自然な定義域\quad&\quad マッピング規則 \quad&\quad 値域 \quad&\quad 到達域\quad\\\hline\\
\quad \mathbb{R}^n \quad&\quad \boldsymbol{A} \quad&\quad colsp(\boldsymbol{A}) \quad&\quad \mathbb{R}^m \quad\\
\\
\hline
\end{array}
参照:列ベクトル行列関数
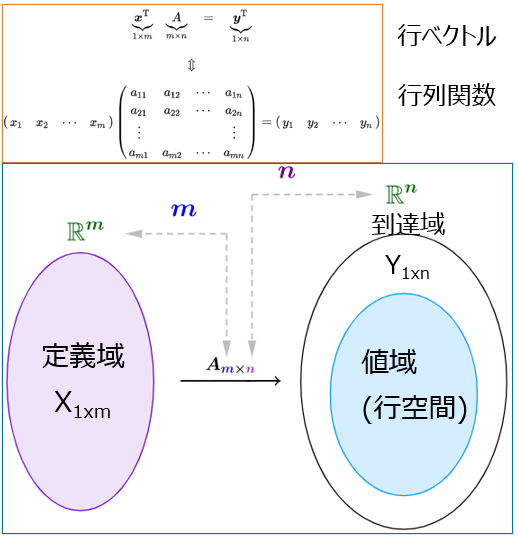
行ベクトル行列関数の値域
考え方は列ベクトルと同じくです、詳細は行ベクトル行列関数の値域に記載があります。
$A$が$m\times n$の行列であれば、自然な定義域での関数$x^T{A}=y^T$四つ要素が:
\begin{array}{c|c|c|c}
\hline
\quad 自然な定義域\quad&\quad マッピング規則 \quad&\quad 値域 \quad&\quad 到達域\quad\\\hline\\
\quad \mathbb{R}^m \quad&\quad \boldsymbol{A} \quad&\quad rowsp(\boldsymbol{A}) \quad&\quad \mathbb{R}^n \quad\\
\\
\hline
\end{array}
行列のランク
自然な定義域内において、行列関数の値域を知ることで、
- 列ベクトル行列関数$A\boldsymbol{x}=\boldsymbol{y}$の値域の次元数は列ランクであり、
- 行ベクトル行列関数$\boldsymbol{x}^\mathrm{T}A=\boldsymbol{y}^\mathrm{T}$の値域の次元数は行ランクであることが分かります。
行ランク=列ランク=ランクであるため、自然定義域内では、ランクは行列関数の値域の次元数と同じです。
-
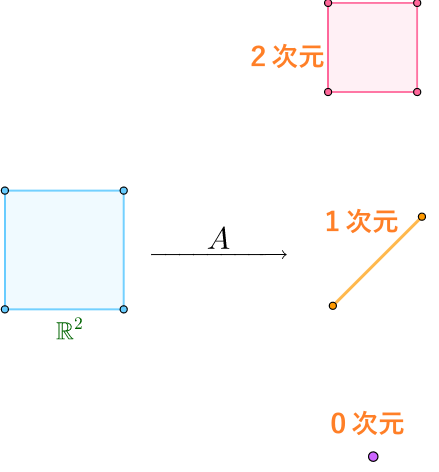
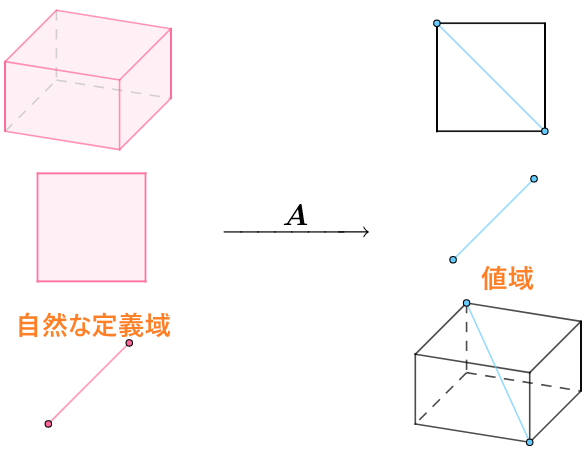
ランクが$2$: $A$の自然な定義域の次元数がいくら関係なく、$rank(A)=2$であれば、値域のランクが$2$になります。
-
同様:ランクが$1$: $A$の自然な定義域の次元数がいくら関係なく、$rank(A)=1$であれば、値域のランクが$1$になります。
行列ランクまとめ
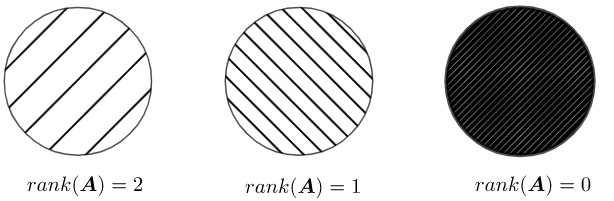
同じ自然な定義域にとって、$rank(A)$が小さければ、値域の次元数が小さくなります。
例えば、
\begin{array}{c|c|c}
\hline
\quad \text{自然な定義域}\quad&\quad \text{ランク}\quad&\quad \text{値域次元数}\quad \\
\hline
\quad \mathbb{R}^2\quad&\quad\begin{aligned}rank(\boldsymbol{A})=2\\rank(\boldsymbol{A})=1\\
rank(\boldsymbol{A})=0\end{aligned}\quad&\quad\begin{aligned}\text{2 次元}\\\text{1 次元}\\\text{0 次元}\end{aligned}\quad\\
\hline
\end{array}
ふるいの穴が大ければ、行列$A$のランクが大きいです、ふるいを通して落ちたもの(値域)が大きいです。
フルランクの行列
とある行列が列フルランク且つ行フルランクであれば、この行列がフルランクの行列と呼びます。また、フルランクの行列が必ず正方行列です。
任意の行列$(A_{m\times n})$にとって、行ランクが列ランクと等しいですので、列フルランクであれば、列ランクが$n$で、行ランクが$m$です。$m=n$ですので、行列$(A_{m\times n})$が正方行列になります。
行ランクが列ランクと等しいが、こちら行列のランクで説明あります。
合成関数のランク
rank(AB)\leq\min\Big(rank(A),rank(B)\Big)
$A$が$m\times r$の行列、$B$が$r\times n$の行列で、列ベクトル行列関数$AB(x)=y$にとって、結合律によれば、以下のが成立しています。
AB(\boldsymbol{x})=(AB)(\boldsymbol{x})=\boldsymbol{y}
$AB$が一つの行列($m\times n$)で、この行列関数の自然な定義域の四つの要素が以下の通りです。
\begin{array}{c|c|c|c}
\hline
\quad 自然な定義域\quad&\quad マッピング規則 \quad&\quad 値域 \quad&\quad 到達域 \quad\\\hline\\
\quad \mathbb{R}^n \quad&\quad AB \quad&\quad colsp(AB) \quad&\quad \mathbb{R}^m \quad\\
\\
\hline
\end{array}

フルランク行列の合成
$P,Q$がフルランクの行列であれば:
rank(PA)=rank(AQ)=rank(PAQ)=rank(A)
参考情報