量子もつれ（エンタングルメント）の仕組みの仮説・視覚化

視覚モデルで見る量子相関

はじめに

私が過去に目にした量子もつれの紹介記事には、次のような説明がありました。
「量子もつれの状態にある2つの量子 a, b を、たとえ何光年離しても、ある時点で a を観測すると、その瞬間に b の結果がわかる。」

さらに、かのアルベルト・アインシュタインさえも、この不思議な現象についてにわかに信じがたく、否定的な見解を示していたと聞きます。

では、なぜそのような不思議なことが起こるのでしょうか。

今回、その謎に対する直観的な可視化モデルを独自にまとめたので共有します。

背景

• 量子ビット（qubit）は、従来のコンピュータのbitと異なり、1量子ビットでとても複雑な状態を持つことができる。
  • 量子ビットを観測すると0として観測される確率がほぼ100%の純粋状態を |0> と表記。
  • 1として観測される確率がほぼ100%の純粋状態を |1> と表記。
  • 0と1どちらが出るか50%ずつくらいの状態を 0と1の重ね合わせ 状態と言う。
  • しかし、それだけではなくもっと多様な状態を持つことができる。
• 不思議な挙動のように見えるのは、複数の量子ビット同士を干渉させると、ある量子ビットの測定結果が他方の結果と強い相関を持つようになることである。
  • 特定のエンタングル状態（例：ベル状態）では、どちらの量子も単体で見ると、0と1が出る確率が50%ずつ程度であるが同じ測定基底で測ると「片方が0なら他方は必ず1（あるいは必ず0）」といった100%の（反）相関が現れる。
  • このように2つの量子間の結果に強い結びつきが生まれることが「遠く離れていても結果がリンクする」という量子もつれの不思議さを生んでいる。

しかし従来の説明は、「相関がある」と抽象的に語られることが多く、なぜ相関が成り立つのか が直感的に分かりにくい。

新しい解釈：周期性による同期

私が提案する理解の軸はシンプルです。

• 複数の量子ビットは、同じ周期で異なるリズムを繰り返すサンプラー（楽器）のようなもの
• それぞれの量子ビットが異なるリズムを叩けるが、繰り返しの周期が同じになるように設計して使用する。
  • 周期の中で同じタイミング（位相）で全く同じリズムを叩いている状態の量子ビット同士は観測結果がいつも同じ。
  • 片方がリズムを叩き、片方が叩かないという譜面で両者がリズムを繰り返しているなら、同じタイミングで観測すると片方が叩いている(観測結果が1)なら、もう片方が叩いていない（観測結果が0）という相関を持つ。
• 量子ビット同士を干渉させると、互いのリズムをサンプラーのようにコピーし合うため相関が生まれる。
• 量子ビットの状態は微細なため物理的に非常にデリケート。操作過程でノイズを受けやすいし、観測するという行為だけでも副作用を与えて状態が変わってしまうことがある。

具体例：波としての量子状態を考える

単純な2量子の例

同じ周期をもつ量子 a, b があり、

• a は位相 0° にあるパルス波
• b は位相 180° にあるパルス波

を持つとします。

横軸 0°〜360°、縦軸 -1〜+1 の 2 次元グラフを円柱に貼り付けて回転させると、こう見えます。

• 正面から見ると a が 1 のとき b は必ず 0

• 180° 回転させると a が 0 のとき b は必ず 1

※いずれの図も直観のための可視化モデルです。実験装置・信号波形を写実したものではなく、エンタングル相関を比喩的に示しています。

つまり、同じ測定基底（測定軸）で観測すると「a が 0 なら b は 1、a が 1 なら b は 0」という強い相関関係が見えてきます。これがエンタングル状態の一つの直感的な表現です。

※この相関は a と b を同じ測定基底で測る場合に現れます。実際のエンタングル状態は確率分布として現れます。

---

QFT（Quantum Fourier Transform: 量子フーリエ変換）の例

ここから少し専門的な例を見てみましょう。

量子コンピュータが持つすごさや可能性を説明する時によく、「現在使われている暗号（RSA-2048）がすぐに解読されてしまうようになる」というような表現で説明されることがあります。
これは量子コンピュータが量子もつれ（エンタングルメント）を利用すると、Shorのアルゴリズムにより暗号解読に必要な素因数分解を効率的に行えるからです。

量子コンピュータで素因数分解を行う際に使われる QFT (Quantum Fourier Transform) というアルゴリズムでは、位相レジスタと呼ばれる複数の量子ビットをアルゴリズムに従って互いに干渉を繰り返したあと、量子ビット列に「周期を示す手がかり」が現れます。

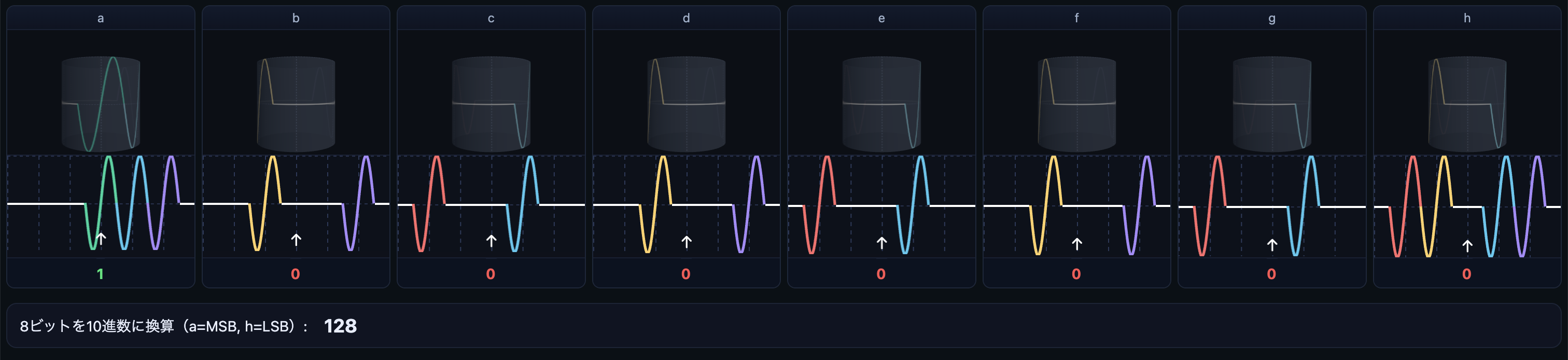
例えば 21 を素因数分解する場合、8 量子ビットの位相レジスタを用意しQFT及び逆QFTの手順で量子ビット同士を干渉させていったあと、それらの量子ビットを観測すると次の値が高頻度で出現するようになります。

      abcd efgh
  0 = 0000 0000b
 43 = 0010 1011b
 85 = 0101 0101b
128 = 1000 0000b
171 = 1010 1011b
213 = 1101 0101b

これらの数は8ビットの位相レジスタで表現できる最大値2^8=256 を 6 分割した値に対応しており、周期性を反映しています。
。周期 r=6 のとき、256/6の付近（0.0, 42.7, 85.3, 128.0, 170.7, 213.3）にピークが現れ、これらに最も近い整数（0, 43, 85, 128, 171, 213）が高頻度で出現します。

量子コンピュータの仕組み上ノイズや周期のばらつきがあるので、確実に0,43,85,128,171,213が必ず出るというわけではないのですが、統計を取ると明らかにこの値になる確率が突出している様子が見えるのだそうです。

• これにより、上記いずれかの値が高頻度で観測され、その値から6回で繰り返す可能性がある値だと判定し、周期r=6 ということが推定できます。このrの値を利用すると素因数分解が容易に解けるのです。

上記以外の値になることもありますが、これらの値は繰り返し実験したときに特に出やすい値となります。
なぜこんな不思議なことが起きるのでしょう？
これはQFT（＋逆QFT）のアルゴリズムの手順で量子ビットと量子ビットを干渉させる手順を踏んだ後、量子ビット同士がエンタングル（量子もつれ）を起こしているためです。
では実際それは具体的にどのような状態なのでしょうか？

ビットごとの波に変換して考える

各ビットを左から順に a b c d e f g h と名付け、出現パターンを並べてみます。
（先ほどのa列〜h列までを「縦読み」して横に並べたのが下記です。）

a=[0,0,0,1,1,1]
b=[0,0,1,0,0,1]
c=[0,1,0,0,1,0]
d=[0,0,1,0,0,1]
e=[0,1,0,0,1,0]
f=[0,0,1,0,0,1]
g=[0,1,0,0,1,0]
h=[0,1,1,0,1,1]

「6 回の観測結果」を 360°周期に対応させるため、1 ステップ = 60° として 1 が出る位置を「パルスがある場所」と見なします。

- a = [0,0,0,1,1,1] → パルス: 180°, 240°, 300°（3本）
- b = [0,0,1,0,0,1] → パルス: 120°, 300°（2本）
- c = [0,1,0,0,1,0] → パルス: 60°, 240°（2本）
- d = [0,0,1,0,0,1] → パルス: 120°, 300°（2本）
- e = [0,1,0,0,1,0] → パルス: 60°, 240°（2本）
- f = [0,0,1,0,0,1] → パルス: 120°, 300°（2本）
- g = [0,1,0,0,1,0] → パルス: 60°, 240°（2本）
- h = [0,1,1,0,1,1] → パルス: 60°, 120°, 240°, 300°（4本）

可視化のイメージ

この結果を先ほどのように円柱グラフ上にプロットしてみると、各量子ビットがそれぞれのリズムでパルスを持つ様子として表せることがわかります。

そして、複数の量子ビットを同じ測定基底（測定軸）で観測すると、a のこのパルスが観測されるタイミングなら、bのパルスが観測されるかされないかが決まる という相関が現れます。（だから、決まった組み合わせ（特定の数値）で観測される確率が高くなる）
これこそが、数式の背後にある「量子もつれ（エンタングル）状態の直感的イメージ」として捉えられるのです。

角度0°からみた時

角度60°からみた時

角度120°からみた時

角度180°からみた時

角度240°からみた時

角度300°からみた時

※いずれの図も直観のための可視化モデルです。実験装置・信号波形を写実したものではなく、エンタングル相関を比喩的に示しています。

これらは、各量子ビットが音楽のサンプラーのように周期的にリズムを繰り返し、2つあるいは複数の量子同士を干渉させた時に互いのリズムが干渉してゆくような挙動をすることを示唆しています。

測定基底の整合

• 各量子は波として揺らいでいるが、同じ測定基底（測定軸）を選ぶことでエンタングル特有の確率的相関が現れる。

• 観測のタイミングは必須条件ではなく、同じ基底なら相関は保たれる一方、異なる基底では相関が弱まったり消えたりする。

• これが「遠隔でも同じ結果が出る」ように見える理由であり、片方の観測結果がもう片方に伝播して結果が変わるわけではない。エンタングル状態は遠隔で情報を書き込む仕組みではなく、測定統計に相関が現れるだけです（非通信定理）。

まとめ

• 量子もつれ（エンタングルメント）は「同周期のリズムが生み出すシンクロナイズ（同期）」と解釈できる。

• 直感的には、「2つの波を同じタイミング（または同じ位相、同じ測定基底（測定軸））で測定したとき、波の山と谷の関係が一致する」イメージに近い。

• この視点を持つと、量子計算における並列性や相関の強さを理解しやすくなる。

  • 様々な量子、測定方式に一般化した言い方をすると、量子もつれ（エンタングルメント）は「測定基底の整合とエンタングル状態の構造」に由来する強い相関として理解できる
  • ここでいう“位相”はTransmon qubitの様相を直観的にイメージするための比喩で、厳密には同じ測定軸を選んだときに相関が最も明瞭になる、という意味

• 最後に強調すると、本稿の“位相とリズム”は直感の足場です。通常、量子力学ではヒルベルト空間・測定理論・Bell不等式などで量子もつれが説明されますが、本記事ではそれらとは別の切り口で量子もつれを考察しました。読者が数式に入る前のイメージ作りとして役立てば幸いです。

  • Bell不等式違反は「単なる周期的隠れ変数モデルでは説明できない」ことを示すといわれており、それを実証する実験結果も報告されています。しかし「量子」の定義は広いため、各実験の対象や条件など精査して、「測定軸をあわせた考え」で考察し、混同を避けて理解する必要があると思います。

今後の展望

• この解釈が量子アルゴリズムの教育や直感的理解に役立つ可能性がある。
• より厳密には量子測定理論の枠組みと突き合わせる必要があるが、初学者がイメージする上で有効な「思考モデル」となるかもしれない。
• 波の比喩を使ったアルゴリズム研究の可能性
  • この波形モデルが新しいアルゴリズム（例: 素因数分解の r 推定）のヒントとなる可能性もありますが、現時点では未開拓の領域です。
  • できた方がいらっしゃいましたらぜひコメントなどで教えてください

注釈

アインシュタインは「量子もつれ」の奇妙さを受け入れず、
「観測前から結果は決まっている（隠れた変数があるはずだ）」と主張しました。

1964年、ジョン・ベルが「もし隠れた変数があって、しかも局所的（離れた場所には瞬時に影響しない）なら、観測結果の相関は必ずある上限を超えない」という数学的不等式を導きました。
→ これが Bell不等式 です。
→ Bell不等式とは「もし結果が観測前から決まっているなら、統計的相関はこの上限を超えない」という制約です。量子実験はこれを破る（違反する）ため、古典的説明では不可能なことが確認されています。

量子には色々な種類があり、当記事の考察はTransmon qubitの仕組みに着想を得て考察した結果です。
当記事での考察は「隠れた周期性で相関を説明する」という直感に基づいています。
これはあくまで思考モデルであり、Bell不等式違反「局所的な隠れた変数による古典的説明では不可能な相関を、実験が実際に示した」という実験結果がいくつも見つかってきています。

Bell不等式違反の確認実験では、光子（フォトン）の偏光状態が最初に使われました。
1982年、アラン・アスペの実験（フランス）は、偏光子を用いた光子のエンタングル状態で Bell不等式違反 を確認しました。

その後も多くの光子ベース実験（偏光・時間ビン・エネルギー時間エンタングルメントなど）が行われ、相関が「古典的位相同期モデル」を超えることが示されました。

近年は光子以外の物理系でもBell不等式違反が観測されています。

当記事の考察は全ての「量子」に当てはまるわけではない可能性があります。

---

おわりに

私は今回、量子もつれ（エンタングルメント）を「同周期のリズムが生み出すシンクロナイズ（同期）」として解釈するアイデアをまとめました。
この視点が読者の理解に新しい切り口を提供できれば幸いです。

補足

「量子」とは具体的に何でしょうか？
一言で量子と言っても、具体的には色々あります。光子だったり、電子だったり。
量子コンピューティングには複数方式があり、その方式毎に利用する「量子」が異なります。
しかしどの方式も量子がもつ多様な特性のうち、何を利用するかを絞ってコンピューティングに利用します。
たとえば、光子だったら「偏光の角度」を用いる方式、電子であれば波の周期の「位相」を用いる方式など。

今回は、現在一番実用化に近づいているTransmon qubitという量子コンピューティングの仕組みを考察して、量子もつれ（エンタングルメント）について考察を行いました。
Transmon qubitでは、超伝導島という2つの薄い長方形の超伝導物質をジョセフソン接合と呼ばれる1本の細い絶縁膜で接合させた構造になっており、この超伝導物質の中に電子が膨大に存在する状態です。絶縁膜の箇所で励起状態が行き来するようになっており、この励起状態の波が2つの島を行ったり来たりすることで波の位相を持ち、位相・電荷の揺らぎの量子状態を保持します。
そう、「量子」というとたった一つの粒のようなものをイメージしてしまいますが、実は、Transmon qubitでは、膨大な数の電子を含む超伝導構造そのものを量子ビットと呼んでいるのです。

この構造から私は、2つの大きなプールを行き来する波の様子をイメージしました。
そのイメージだと、波はプールの端で折り返して反対側の端まで進み、また折り返して戻ってくるということを繰り返します。
そして、波は1つだけではなく、何度も波を作ると、その波が追加され、一定周期でリズムを打つように繰り返します。
このようなことがTransmon qubitの電子のプールの中で、励起状態の波が周期的に打ち寄せてくるものだとイメージしました。

今回の考察を踏まえると、量子コンピューティングに利用可能な量子ビットとは、
同じ周期で、それぞれ独自のタイミングでリズムを打つ楽器のようなものだと例えることもできます。
複数の量子ビットが同じ周期で合奏し、各量子がそれぞれの譜面でリズムを叩いている状態です。

譜面上で同じタイミングでリズムを叩く量子ビット同士は、同じタイミングで観測すると同じ結果。
これが「量子もつれ」「エンタングル」の「直観的な思考モデル」だと私は考えています。

今回例に挙げたのは、360°を60°ずつで割った６拍子のリズムでしたが、
もっと細かく角度を刻むと、交響曲のような長い長い譜面をギュッと一瞬で演奏し切るような状態になります。
なので、音楽の数が無数にあるように、量子ビットの状態も譜面の分解能（＝量子ビット操作の分解能）に応じて非常に多様なリズムを持つことができるため多様な状態を持てるのです。

この考察が量子コンピューティングを学ぶ方々の理解の一助になれば幸いです。
また、万が一この予測が誤っていた場合、皆様の学習を阻害する結果にならないことを祈るばかりです。

参考文献