増川 直裕
■日本の人口減少が止まらない
先日、昨年(2021年)の出生数は過去最少になり、死亡数は戦後最多になったとの報道を耳にしました。これらの原因として、コロナウィルスの影響から妊娠を控える方がいた、コロナに関連した死亡が多かったことが挙げられていました。
そこで、昨年だけではなく、過去にも遡って出生数と死亡数を見てみましょう。下のグラフは、2014年～2021年の年ごとの出生数、死亡数をグラフにしたものです。
青色の折れ線が死亡数を、赤色の折れ線が死亡数を示しています。
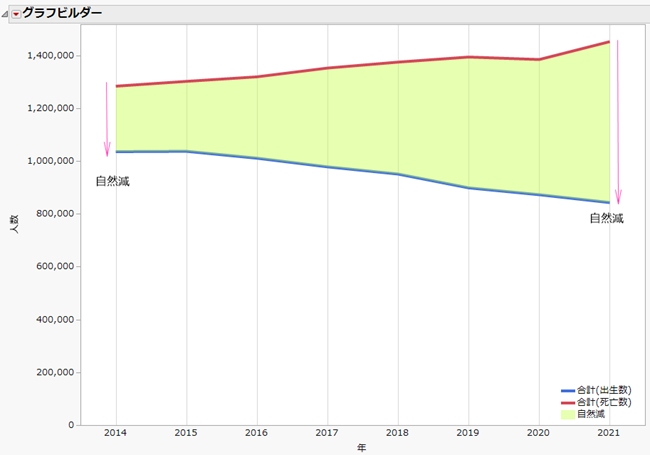
データの出典：厚生労働省 人口動態統計（速報値）
青色で示した出生数は明らかな減少傾向がみられ、赤色で示した死亡数は増加傾向になります。その結果、緑色で囲んである自然減（出生数と死亡数の差）は、年ごとに大きくなるばかりです。近年では、2020年の自然減は約51.2万人でしたが、2021年は約60.9万人となり、前年比で約16%増となりました。
今後、日本の人口が減少していくことは、以前から言われていたことなので分かってはいましたが、減少のスピードが速いかなと感じています。仮に1年で60万人減るとなると、10年で600万人減るわけです。ただ、1年で60万人減は現在の状況であり、今後、減少数は増加する可能性の方が高いはずです。
今後の出生数や死亡数は、さまざまな外部状況（ウィルスや社会保障制度など）により変化する可能性があるので、予測するのは難しいです。ただ、過去のデータを使って、近い未来である今年(2022年)の予測はそれなりにできるかもしれません。
本記事では、JMPの機能として搭載されている「時系列分析」の季節ARIMAモデルを使って、過去のデータ（2014年～2021年）から、2022年の出生数、死亡数を予測してみます。
■季節ARIMAモデルのあてはめ
ARIMAモデルは、時系列データを使って将来を予測する方法として広く使われています。太陽の周期といった自然現象や在庫管理、経済指標、株価など幅広く使われていることもあり、今回の出生数、死亡数のデータでも用いてみます。
実は、出生数、死亡数ともに周期性があります。以下のグラフは、2014年～2021年の月ごとの出生数（青色）、死亡数（赤色）です。
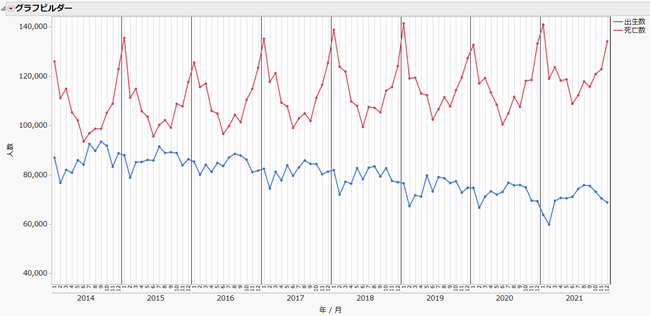
例えば死亡数の場合、どの年も1月が最も多く、6月が最も少なくなっています。出生数は、多くの年で8月が最も多く、2月が最も少なくなっています。そこで、この周期性を考慮し、月ごとのデータに対し季節ARIMAモデルをあてはめ、2022年の予測をしてみます。
■季節ARIMAモデルにおける次数の決定
本記事では、ARIMAモデルの詳細な説明は省略しますが、実務上、ARIMAモデル、季節ARIMAモデルをあてはめる際、やっかいな点はモデルの次数を決めることです。
以下は、JMPで季節ARIMAモデルをあてはめるときの指定ウィンドウですが、あてはめる際、ARIMAの次数(p,d,q)、季節ARIMAの次数（P,Q,R）、1周期における時点数（周期）を指定する必要があります。
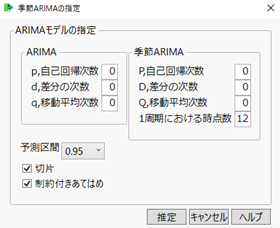
今回の出生数と死亡数において、周期は12(12か月周期)で良いですが、それ以外の次数（自己回帰、差分、移動平均）を決めなくてはなりません。
これらの次数は、時系列分析で出力される自己相関プロット、偏自己相関プロット、差分のプロットなどからヒントを見つけることはできますが、明確に次数を見つけることが難しいことも多いです。
JMPでは、”さまざまな次数のモデルをあてはめて、それらのモデルの良さを比較することにより次数を決める” ことができる機能があります。
そこで、この機能を活用し、次の手順（ステップ1, ステップ2）で、2022年の出生数、死亡数の予測をしていきます。
ステップ1 . 季節ARIMAモデルの次数決定
- 2014年～2020年を学習データとして、さまざまな次数の季節ARIMAモデルをあてはめる。
- 2021年を検証データとして、あてはまりを評価する統計量(RMSE)を使い最適な次数を決定する。
ステップ2. 決定した次数を使って2022年を予測
手順1.で決定した最適な次数を用い、2014年～2021年に対して季節ARIMAモデルをあてはめ、2022年を予測する。
■ステップ1. 季節ARIMAモデルにおける次数の決定
JMPの「時系列分析」において、「複数のARIMAモデル」の機能を使うと、次のように、ARIMAモデルにおける次数を動かす幅を指定することができます。
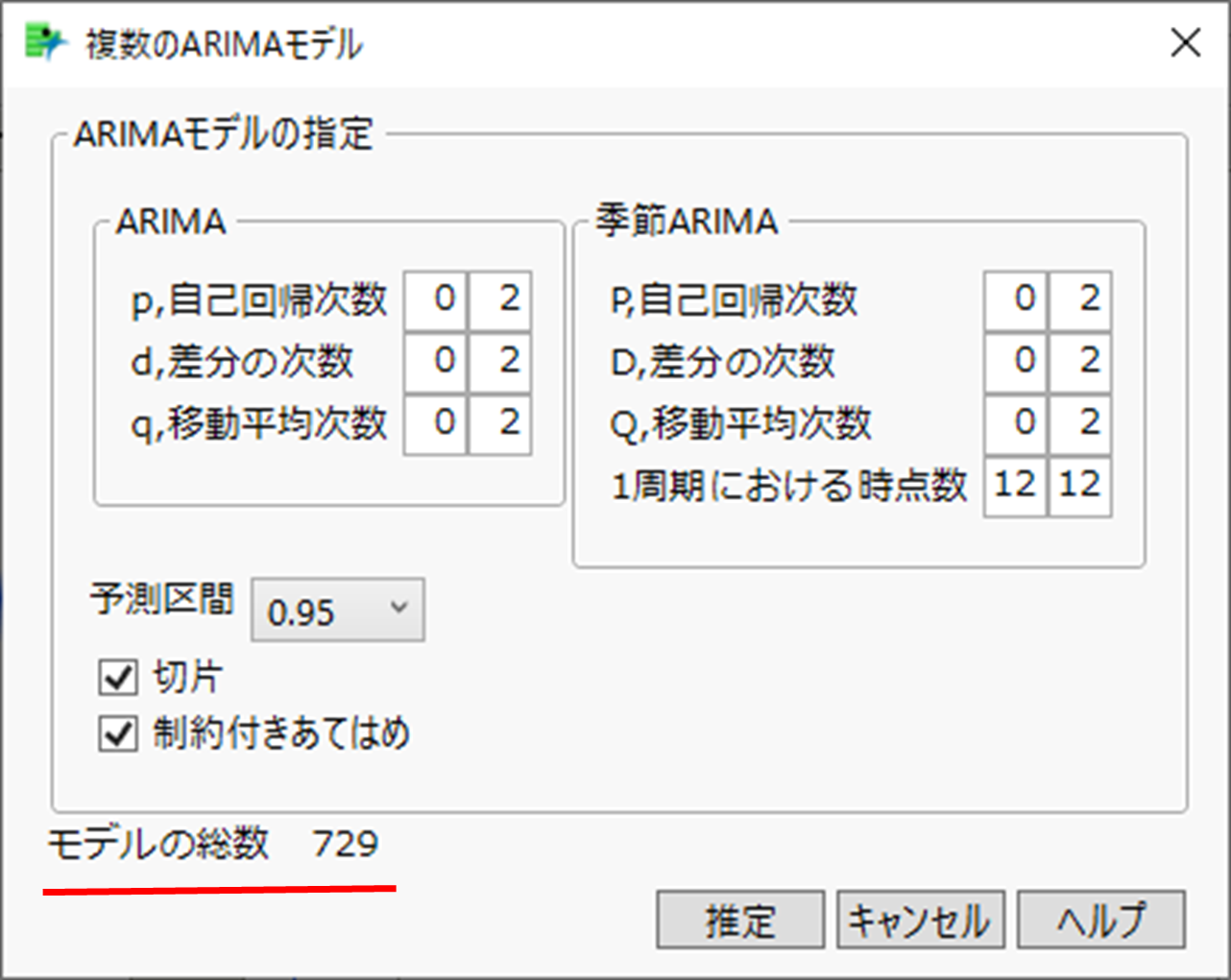
ここでは、ARIMAの3つの次数、季節ARIMAの3つの次数を、それぞれ0から2まで動かしていくといった指定をしています。
すなわち、 p,d,q,P,D,Q の次数に対し、それぞれ0,1,2の3パターンを考え、それらすべての組み合わせをあてはめることになります。組み合わせの数は3の6乗なので、モデルの総数は729パターンになるのです。
[推定] ボタンをクリックすると、729ものモデルをあてはめるので、少々時間がかかりますが、しばらくすると、次のような、モデルの良さを比較したレポート「モデルの比較」を得ることができます。
このレポートにある「モデル」は、以下の記述における次数を示しています。
季節ARIMA(p,d,q)(P,D,Q)12
最後にある”12”は周期数を示し、今回の例では12に固定しています。
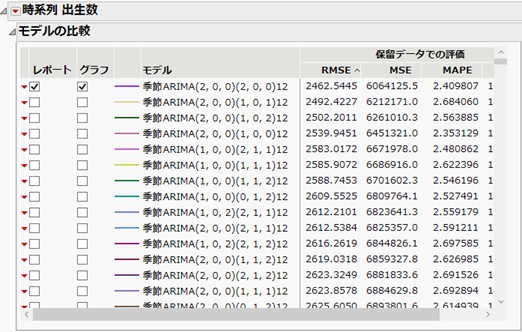
上に示した「モデルの比較」レポートでは、各モデルを学習データにあてはめ、検証データに対する評価指標（保留データでの評価）が示されています。デフォルトでは、検証データに対する誤差の標準偏差（RMSE）が小さい順に並んでいます。
検証データのRMSEが小さいほど良いモデルと考えると、レポートの上から下にわたり、良いモデルの順に並んでいることになります。
上図は出生数のデータに対するあてはめであり、このときの一番良いモデルは、季節ARIMA(2,0,0)(2,0,0)12 であることがわかります。
実際にこのモデルをあてはめたときのグラフを示します。黒い点は出生数の実測値であり、紫色の折れ線が、このモデルにおける予測値を示しています。紫色で塗りつぶされた区間は、予測における95%信頼区間です。
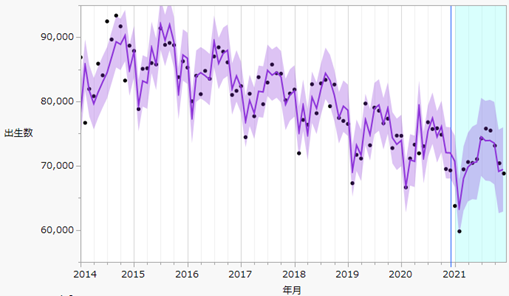
グラフ右側の2021年が検証データであり、黒い点である実測値と、モデルで求められた予測値から誤差(RMSE：誤差の標準偏差) が計算され、その値が、他のモデルと比較したとき最も小さかったのです。
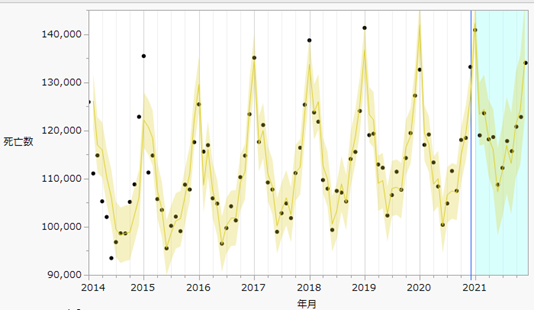
同様に、死亡数についてもモデルをあてはめてみると、季節ARIMA(0,1,1)(2,0,0)12 が最も良いモデルとなります。下図は、このモデルをあてはめたときのグラフです。
■ステップ2. 決定した次数を使って2022年を予測
ステップ1より、次のように最適なモデルが決まりました。
出生数： 季節ARIMA(2,0,0)(2,0,0)12
死亡数： 季節ARIMA(0,1,1)(2,0,0)12
今度は、2014年～2021年のデータ（今現在あるデータ）について、これらのモデルをあてはめ、2020年の月ごとの予測値を算出します。
その後、2022年の月ごとの予測値を合計し、2022年の予測値とします。
このプロセスを経て得られた2022年の出生数、死亡数の予測値を、本記事の最初に示したグラフに追加しています。
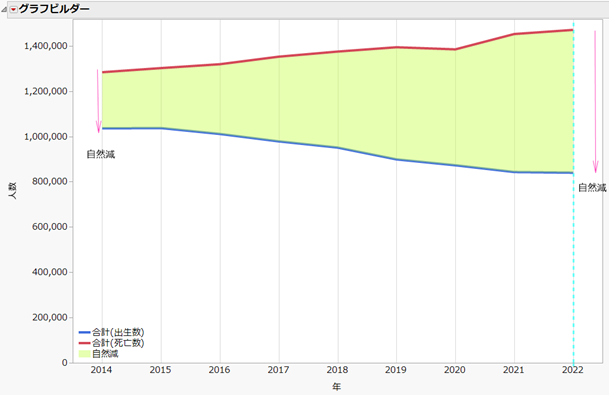
2022年における出生数の予測値は839,796人、死亡数の予測値は1,470,462人となり、やはり、出生数は2021年に対して減少、死亡数は増加するといった予測になります。
これらの予測から、2022年の自然減の人数は約63.1万人になり、前年比で約3.4％増加することになります。
日本において、今後の人口減少は致し方ないところなのかもしれませんが、人口が減るということは、労働力不足、消費の減少等を引き起こし、日本が経済的に弱くなる恐れもあります。
コロナが終息に向かえば、人口減少の問題は少し改善するかもしれません。さらに、医療が進歩すれば、死亡数は少なくなるかもしれません。しかし、日本の未来を考えると、やはり出生数を増加させることですね。今後の社会政策に期待したいところです。
■さあ始めよう！
JMPの全機能を30日間試せるトライアル版で、データからさらなる情報を導き出せることを実感してください。
ダウンロードはコチラ！
■JMPについて
JMP（ジャンプ）は世界中のエンジニア、データアナリストに選ばれているインタラクティブで可視的なデータ分析ツールです。