はじめに
エキサイトの新卒1年目エンジニアの伊藤です。
adventCalendar22日目は効果検証の難しさをまとめて, その解決をPythonで実践します。
効果検証を阻む2つの難しさ
Webサービスの運用において売上アップのためのキャンペーンは欠かせない施策の1つです。
私が携わっているサービスでもサービス内で利用できるコインを配布する形式のキャンペーンをよく行います。
この時, より効果のあるキャンペーンを見つけるPDCAを回したいはずですが, キャンペーンの効果測定は以下の2つの難しさに阻まれることが多いです。
1. セレクションバイアス
例えば, 月末の売上落込みへの対策として月末キャンペーンを実施したとします。
このとき得られるデータは「月末の落ち込み」と「キャンペーン効果」が合わさった値となります。
セレクションバイアスとは何らかの条件で括った集合とそれ以外の集合の潜在的な差を表します。
この例の場合, 月末集合とそれ以外の集合との売上差にあたります。
キャンペーンの効果を正しく測るにはこの差をうまく取り除かなければなりません。
2. ある日の売上データは1つしか存在しない
一般に, 介入による効果の違いを検証したいのであれば, 介入ありのデータと介入なしのデータを十分な数揃えて, 検定なりベイズ推定なりを行えばわかります。しかし, 2020/12/20にキャンペーンを行ったとしてその売上データは1つしかありません。これは以下の2つの問題を引き起こします。
1. 2020/12/20にキャンペーンを行わなかった場合のデータを手に入れられない
2. 検定やベイズ推定のための十分な数のデータを得られない
こちらは時系列データが定常性を持つという仮定を置くことで解消します。詳しくは後述します。
※介入: キャンペーンなど何かしらのアクションを集団に対して行うこと
効果検証の難しさを解消する
重回帰分析によりセレクションバイアスを省く
セレクションバイアスを省く方法は傾向スコア・差分の差分法・回帰不連続デザインなどいくつかありますが, 本稿では基本的な回帰分析を使用します。なお, 重回帰分析・最尤推定の知識を読者が有しているものとして話を進めます。
基本的な方針は, 介入変数(キャンペーンを行ったか否か)と共変量(月末か否か)を含むモデルを構築します。
これにより, 介入と共変量の効果を別々に推定します。
定常性という仮定
定常性とは時系列データが以下の2つの条件を満たすことです。
- 期待値は時点によらず一定である
- 自己共分散は時点によらず時間差のみに依存する
つまり, 単に複数時点の平均や分散をとれば, それがそのまま「特定時点の期待値や分散の推定量」と見なすことができます。
しかし, 期待値が時点によらず一定とはつまりトレンドがないことを表します。そのような時系列データは中々ないため基本的には前時点のデータとの差分をとることにより, 定常過程へと変換します。差分をとった時系列データ(差分系列)が定常性を持つか否かはKPSS検定などを使用して知ることができます。
これにより, ARMAモデルを使った時系列回帰分析が可能になります。
※厳密に定常性とは弱定常性と強定常性とがあります。本稿で定常性とは弱定常性のことを表します。
※ARMA(ARIMA)モデルは古典的な時系列回帰のモデルです。本稿では詳しく解説しませんが興味がある方は調べてみてください。
効果検証実践
モデル
今回は時系列回帰で一般的なARIMAXモデルをパラメータ(1,1,1)で採用します。
本来はAICなどの指標を使ってモデル同定を行わないと行けませんが今回の趣旨はそこではないため最も単純なパラメータ(1,1,1)を使用します。
ARIMAX(1,1,1)をモデル式で表すと以下のようになります。
y_t = \phi y_{t-1} + \theta\epsilon_{t-1} + c + \beta_{campaign}x_{campaign} + \beta_{monthend}x_{monthend} + \epsilon_t
$y_t$: t時点での売上
$c$: トレンド
$\phi$: t-1時点の売上が及ぼす影響
$\theta$: t-1時点の外因性ノイズが及ぼす影響
$\beta_{campaign}$: キャンペーンが売上に及ぼす影響
$\beta_{monthend}$: 月末が売上に及ぼす影響
$x_{campaign}$: キャンペーン日に1それ以外の日に0をとる2値変数
$x_{monthend}$: 月末(毎月27日以降)に1それ以外の日に0をとる2値変数
$\epsilon$: 外因性ノイズ
推定
それでは上記の話をコードを踏まえて実践します。
今回使用するライブラリー群です。
import pandas as pd
import numpy as np
import statsmodels.api as sm
推定用に架空のデータを生成します。
特にこれといったこだわりはありませんが, 「2020/1/1にローンチしたサービスで4月に月末のユニークユーザー数が低下することがわかり, 4月から月末のキャンペーンを行い始めた」みたいな想定をしました。
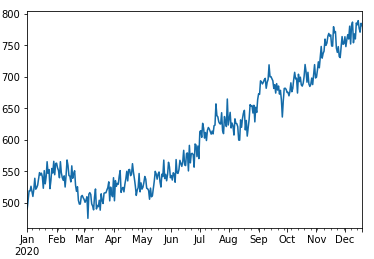
月末に平均10人ほど利用者がいなくなり, キャンペーンの効果は平均して+10人ほど利用者を引き寄せるように生成しています。なお, 初期ユーザー数は500人ほどとします。
# 2020/1/1~2020/12/19までの値を生成
df = pd.DataFrame(index=pd.date_range(start='1/1/2020', end='12/19/2020', freq='D'))
# 月末を表す2値変数の追加
df['monthend'] = (df.index.day >= 25).astype(int)
# 月末キャンペーンを表す2値変数の追加
df['campaign'] = ((df.index.day >= 27) & (df.index.month >= 4)).astype(int)
# UU数データの生成
trend = np.random.normal(loc=1, scale=5, size=len(df)).cumsum()
monthend = df['monthend']*np.random.normal(loc=10, scale=5, size=len(df))
campaign = df['campaign']*np.random.normal(loc=10, scale=5, size=len(df))
noise = np.random.normal(loc=0, scale=10, size=len(df))
df['uu'] = trend - monthend + campaign + noise + 500
# 生成したUU数の推移をプロット
df['uu'].plot()
まずはキャンペーンとそれ以外の日で単純な平均値の差分を出してみます。
# 差分系列で考える
df['diff'] = df['uu'].diff()
# キャンペーン日の平均とそれ以外の日の平均の差
campaign_effection = df.loc[df['campaign'] == 1, 'uu'].mean() - df.loc[df['campaign'] == 0, 'uu'].mean()
display(campaign_effection)
28.85179016200425
外因性ノイズとセレクションバイアスの影響で, めちゃくちゃな値が出てしまいました。
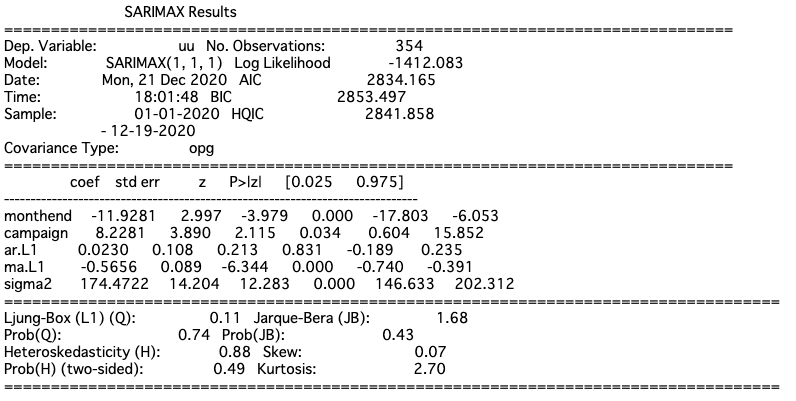
では, 実際に上記のモデルを最尤推定して結果を出してみます。
result = sm.tsa.SARIMAX(endog=df['uu'], exog=df[['monthend', 'campaign']], order=(1,1,1)).fit()
print(result.summary())
月末が-11人, キャンペーン効果が+8人と誤差はあるもののしっかり推定されていそうです。
最後に
実はよしなに飛ばした問題がいくつかあるため, これをそのまま業務適用するにはまだまだ難しい段階です。
しかし, 今回趣旨とした「セレクションバイアス」と「ある日の売上データは1つしか存在しない」という問題に対しては重回帰分析と定常性という2つのキーで対処することが可能ですので参考にしていただけると幸いです。
最後に, 弊社の採用情報をになります。
https://www.wantedly.com/companies/excite
参考
- 効果検証入門 正しい比較のための因果推論/計量経済学の基礎
- 時系列分析と状態空間モデルの基礎 RとStanで学ぶ理論と実践