概要
昨今ビックデータやそれを活用するAI技術などが特に技術的な注目を浴びていますが、これに伴って個人情報が侵害される危険性も増しました。しかし、個人情報を保護するような技術はAIなどの技術に比べて軽視される傾向にあると思います。
僕はそんな個人情報を保護する技術、匿名化技術を研究しています。匿名化技術をより皆さんに理解して頂きたくて、この記事を書くことに決めました。
注意
この記事を書くにあたり、できるだけ正しい記述を心がけますが、内容のわかりやすさを優先して僕の解釈を混ぜています。よって、不正確な部分が生じていることがあると思います。お気づきの際は適宜コメント等で指摘してくださると大変助かります。
そもそも匿名化とは?
匿名化という言葉が指す行為とは「データから名前や社会福祉番号などのすぐに個人が特定されるような情報を削除すること」と判断される方が多いと思います。しかし、例えば位置情報などは全く同じ軌跡を持つ個人が複数いることは考えにくいですし、一つでは個人を特定できない情報も集まれば個人を特定するに足る情報になりえます。つまり、全ての情報が個人特定につながる可能性があるため、それを踏まえて匿名化する必要があります。
名前や社会福祉番号などのすぐに個人が特定される情報を識別子(identifier)、それ以外の集まることで個人の特定につながる可能性のある情報を準識別子(quasi-identifier)と呼びます。匿名化技術関連の議論をするときは、前提として識別子の情報は消されることになっているのが普通です。以下でも識別子の情報は既に消されているとして話します。
| 該当例
:-- | :-- |
識別子 | 名前、社会福祉番号といったIDの類 |
準識別子 | 位置情報、購買履歴、誕生日、住所、性別、年齢、年収 その他諸々場合による |
補足
正直な話、識別子に関しては個人情報保護法があり定義されている節はありますが、準識別子に関してはどこからどこまでがそれにあたるのかには議論があると思います。例えば、性別を例として挙げましたが、性別なんて男と女(最近ではそれ以外)くらいです。確かに、個人を特定する材料としてはあまりにも弱い要素です。しかし、誕生日、性別、郵便番号から個人を特定し、病歴に関して情報を得たことを報告する論文もあります。ただし、個人的には、どれが識別子と類似する性質があるという意味での準識別子であるのかという議論よりもこの情報は他から観測が可能であるかどうかの可観測性について議論する方が有益だと思います。
結局のところ、例え、ゲームで使っているアバターの行動履歴でも個人に帰属する情報であればすべて識別子と似た性質を持つため準識別子として扱えます。では、考慮しなくても良い要素とは何かと考えたとき、大事なのはそれが攻撃者に観測される可能性があるのかだと思います。先に例で言えば、普通ゲーム内のアバターの行動など、ゲーム会社以外知りえないとすれば、準識別子として扱う必要はないですし、ゲームでもストーカがいると思えば、それも立派な準識別子です。
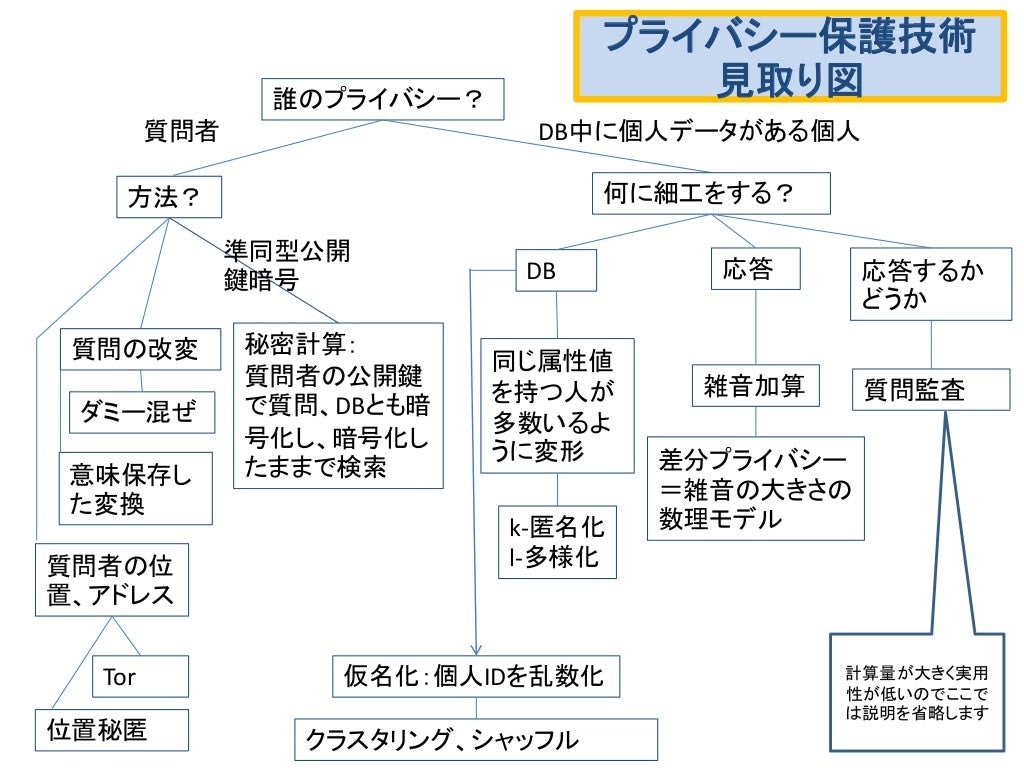
今回お話するのは、タイトル通り【k匿名性, l多様性,t近接性,差分プライバシ】についてになります。これらの技術的な関連は中川裕志先生のスライドにあった図が分かりやすいので、それを紹介します。
引用元:https://www.slideshare.net/hirsoshnakagawa3/it-78784457
k匿名性、l多様性(t近接性)は図中央ちょい右に配置され、差分プライバシはその右にいます。ちなみに、匿名化と匿名性で表記が図と違いますが、これは匿名化が匿名性を与える手法のことを言っているだけで、「方法」と「性質」という意味での違いです。今回はアルゴリズムについての解説ではないので、匿名性の紹介となります。
全て右に配されているのは、本記事がデータベース内の個人の情報をどう細工して隠すかについてのみにフォーカスしているためです。
k匿名性
おそらく最も有名な匿名性がこのk匿名性です。
k匿名性の定義は
全ての個人のデータに対して、その準識別子が全く同一の個人が少なくともk人以上存在する
というものです。
例えば、以下のようなテーブルのデータがあったとしましょう。
表1 病気データ
| id | 年齢 | 性別 | 病気 |
|---|---|---|---|
| 1 | 23 | 男 | 肺炎 |
| 2 | 32 | 男 | 肺炎 |
| 3 | 78 | 男 | 胃ガン |
| 4 | 72 | 女 | リウマチ |
idは説明のために付した数字で実際にはないものと思ってください。仮に、この4人しか登録されていないテーブルに太郎がいることがわかっており、太郎が78才の男であることがわかっているとすれば、すなわち太郎は id=3 の人物で、病気が胃ガンであると発覚します。これでは、匿名性を保てないわけです。
そこで、k匿名性ではこの「病気」という個人情報を守るためにそれ以外の準識別子(年齢、性別)について全く同一の個人がいるように加工します。例えば以下のように上のテーブルを k=2 の匿名加工をします。
表2 k=2匿名化された病気データ
| id | 年齢 | 性別 | 病気 |
|---|---|---|---|
| 1 | 20~40 | 男 | 肺炎 |
| 2 | 20~40 | 男 | 肺炎 |
| 3 | 70~80 | * | 胃ガン |
| 4 | 70~80 | * | リウマチ |
*は情報なしという意味です。こうすれば、太郎が胃ガンかリウマチかはわからなくなります。これは病気以外の準識別子にあたる年齢、性別がすべての個人で2人以上存在しているためです。つまり、k匿名化によって病気という個人情報を守ることができました。しかし、その代わり、生のデータに比べてデータが劣化しているという具合です。
k匿名性の問題
k匿名性は機密情報が「個人が特定されない」ことに頼って保護されていました。しかし、ここには問題があります。例えば、一郎が23才の男であるとわかるだけで表2からも一郎が肺炎であることが分かります。これは id=1,2 どちらも同じ病気を持っているため起こる問題です。確かに、k匿名性はidの判別に関してはk人以下に絞ることを許さない状態を作ることができます。しかし、idについて保護しただけで、機密情報そのものについて保護できるかは別問題なのです。
補足
k匿名性がidについてのみ保護し、実際には機密情報を保護していないことが問題であると書きましたが、実際にこれが問題かどうかには議論があります。多くの人が持つような情報、例えば、日本に住む人の国籍が日本である等の情報はほとんど価値を持たない当前の情報です。これと同様に考えて、表2の状態であれば、若い男性のほとんどが罹る肺炎という病気はほとんど価値がない情報だと言えるでしょう。つまり、若い男性といえば肺炎と言える状態なので、これが暴露されることに対するダメージそれなりに少ないはずです。乱暴な言い方ではありますが、k匿名性が抱える問題とは、k匿名性がこれは個人情報ではないと判断したものについての話なのです。
l多様性、t近接性
k匿名性の問題を解決するために考えだされたのが、l多様性、t近接性です。k匿名性が準識別子に注目して、機密情報を保護したのに対して、今度は機密情報そのものに注目しているという具合です。ただし、どちらもk匿名化が施されたデータに対して追加で考える匿名性で、k匿名化工した後にできる準識別子を同一とするデータ群Q*ブロックの機密情報ついて考えます。
l多様性
定義は
任意のQ*ブロックが l種類以上の機密情報を持つこと
であり、例えば、表2ではid=1,2のQ*ブロックでは l=1, id=3,4では l=2 となります。l多様性を満たすことはk匿名性の問題を解消する1つの手段になります。
しかしながら、l多様性は機密情報の種類に注目しているため、例えば、病気の代わりに住所などのより一人一人が異なる値を持つようなもの(連続値)の場合の対処や、Q*ブロック内での機密情報の頻度や分布に関して全く考慮されない問題があります。その点に関して改善されたのが次のt近接性になります。
t近接性
Q*ブロック内の機密情報の分布が全体の機密情報の分布とどの程度まで離れているかについて保証する匿名性です。定義は
任意のQ*ブロック内の機密情報の分布と全体の機密情報の分布の差がt以下である
となります。k匿名性やl多様性がその個数の下限についてだったのに対して、t近接性は差の上限を保証している点に注意が必要です。
ここで言う「分布の差」については解釈が使う人に依存しているようで、例えば
- 頻度の差の絶対値
- KL距離
- Earth Mover's Distance(EMD)
などがあげられるようです。t近接性が定義された論文では、EMDを使用することが、EMDが機密情報間の”距離”を定義している意味で妥当だとしています。
t近接性はl多様性に比べて応用先が広くなる特徴があります。また、全体の分布と比較する点は、攻撃者が知っている知識をデータ全体の機密情報の分布としたとき、攻撃者が得られる最大知識量を制限しているとも解釈でき、大変興味深い手法です。
ただし、一般にk匿名性よりもさらに厳しく匿名性を追及する匿名性であり、攻撃者が得られる情報量を制限するということは、そのままデータ利用者の得られる情報も制限されることに繋がるため応用には注意が必要になります。
差分プライバシ
これまでの議論と一味違うのがこの差分プライバシです。
k匿名性がデータ全体に匿名加工を施したのに対して、差分プライバシではクエリに対して加工を施します。例えば、「平均値を知りたい人には正しい値を教えるが、データ全体が知りたいという人にはかなりの処理を加えたデータを渡す」といった具合に、教える情報(クエリ)毎に与える加工を変えます。
例えば次のような事例が考えられます。
データとして以下の表3があるとします。
表3 年収データ
| 氏名 | 年収(万円) |
|---|---|
| 太郎 | 500 |
| 次郎 | 200 |
| 三郎 | 800 |
このデータを持っている事業者に対して、「年収の合計を教えて」とクエリ(質問)を投げます。すると、事業者は「1500万円」と答えを返すわけです。これ自体にはそこまで問題はありません。
しかし、この表3に1人足されたデータ表4を考えましょう。
表4 年収データ+
| 氏名 | 年収(万円) |
|---|---|
| 太郎 | 500 |
| 次郎 | 200 |
| 三郎 | 800 |
| 四郎 | 900 |
これにも同様に「年収の合計を教えて」とクエリを投げます。すると、今度は「2400万円」と答えを返すわけです。
もし、攻撃者は先程のクエリの答え「1500万円」と今回の答え「2400万円」を知っている場合、四郎の年収について把握することが可能です。
$$四郎の年収 = 2400 - 1500 = 900$$
そりゃ、そうだろうという感じですが、これで四郎の年収が明らかになるのは事実です。しかし、なら「合計」というクエリに答えなければ良いだけなので、あまり腑に落ちない方もいるはず。ただし、その場合、答えても良いクエリとダメなクエリはどのように区別を付けるべきなのでしょうか?そもそも、答えて良いクエリとダメなクエリは明確に白黒つけられる問題とも思えません。例えば、同じ平均という統計量でも100万人の平均と2人の平均では意味が違います。
ここで、差分プライバシが用意した概念が敏感度(Sensitivity)です。敏感度とはクエリに対して、どの程度、個人の情報がクエリの答えに寄与しているかを表現する値で、クエリごとに決定されます。これが小さければ、個人情報としての価値がないので、公開しても問題ないわけです。
敏感度にもL1敏感度やL2敏感度というように種類があるのですが、最も簡単なL1敏感度について説明します。
L1敏感度
まず、準備として色々定義しましょう。
クエリ$Q$についてデータベース$D$を引数に取り答えを与える関数 $f_Q(D)$
データベースDに隣接するデータベース $D^{'}$
ここで、データベースとは表3のようなもののことで、隣接するデータベースとは表3に対する表4のことです。つまり、1人分だけデータベースの中身が違うもののことを指します。そのうえでL1敏感度$\Delta_1$とは
$$\Delta_1 =max_{D,D^{'}} ||f_Q(D) - f_Q(D^{'})||_1 $$
となります。$|・|_1$は絶対値(L1ノルム)を与えます。
つまり、隣接するデータベース間でクエリの結果の差の最大値がL1敏感度です。このように定義することで、クエリQに個人情報が寄与する度合いを定量的に測ることができます。
ただし、注意したいのは、この定義では先ほどの年収の合計などに対して敏感度がうまく定義しづらいことです。
問題は年収という要素に上限がないためです。非現実ですが、理屈の上では、いくらでも年収はあり得るはずです。そうなるとL1敏感度も無限大に大きくなります。この問題に対しては普通、年収に対して1億円などの上限を設け、それ以上の人は1億円に丸められて記録されるとして対処します。
では、N人が登録されている年収のデータベースついて、平均年収と合計年収を求めるクエリに対して、それぞれL1敏感度を求めてみましょう。
ただし、年収は上限1億円とします。
\Delta_{1,平均} =max_{D,D^{'}} ||f_{平均}(D) - f_{平均}(D^{'})||_1
= max_{D,D^{'}} \frac{||SUM(D)-SUM(D^{'})||_1}{N}
= \frac{1億円}{N}
\Delta_{1,合計} =max_{D,D^{'}} ||f_{合計}(D) - f_{合計}(D^{'})||_1
= max_{D,D^{'}} ||SUM(D)-SUM(D^{'})||_1
= 1億円
平均の敏感度がNに対して反比例するのに対して、合計は常に1億円を取ります。つまり、1億人に対してのレコードに平均を聞く分には、一個人はその平均値に1円程度の寄与しかしていないという訳です。
メカニズム
差分プライバシが敏感度を定義して、クエリに対する一個人の寄与度を測ることはわかりましたが、実際はどのようにそれを使って個人情報を隠せば良いのでしょうか?
ここで登場するのがメカニズムです。このメカニズムを敏感度に応じて適応することで、プライバシを保護することができます。本来であれば、メカニズムはどのような方法でもいいのですが、現在の研究レベルでもほとんどがノイズを付加するメカニズムになっています。
このメカニズムの中でもっとも簡単なものがラプラスメカニズムです。
名前の通り、ラプラス分布に従うノイズによってクエリ結果をぼかします。具体的にどのような大きさのノイズを乗せるか、つまり、ノイズのスケール$\sigma$がどの程度か以下の式で求まります。
\sigma = \frac{\Delta_1}{\epsilon}
非常に単純な式ですが、ここで出てくる$\epsilon$は差分プライバシにおけるプライバシ基準の度合いを表す値です。k匿名性などの$k$異なり、必ず正の値を取り、0に近いほどプライバシが保護されます。$\epsilon$が大きい時は$\sigma$が小さくなり、逆に$\epsilon$が小さいときは$\sigma$が大きくなるので直感的にもわかりやすいと思います。
差分プライバシ基準ε
さて、$\epsilon$が出てきましたが、こいつはどのような基準なのでしょうか?少し話を差分プライバシの根幹の方に戻してみようと思います。
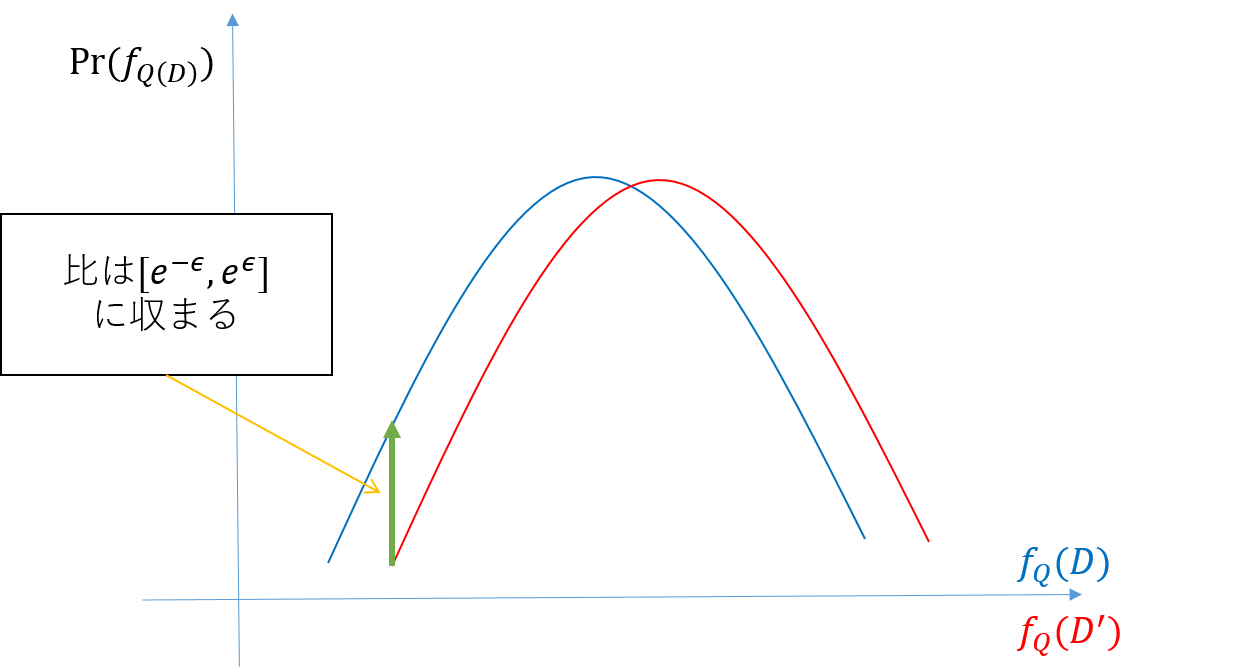
実は、そもそも、差分プライバシはデータベースDへのクエリQの返り値$f_Q(D)$が任意の$f_Q(・)$が取りうる部分集合$O$と隣接データベース$D^{'}$に対して、以下の式を保証するものだったのです。
e^{-\epsilon}Pr(f_Q(D^{'})\in O) \leq Pr(f_Q(D)\in O) \leq e^{\epsilon}Pr(f_Q(D^{'})\in O)
なんだが、扱いにくそうな式ですが、言っていることは単純です。
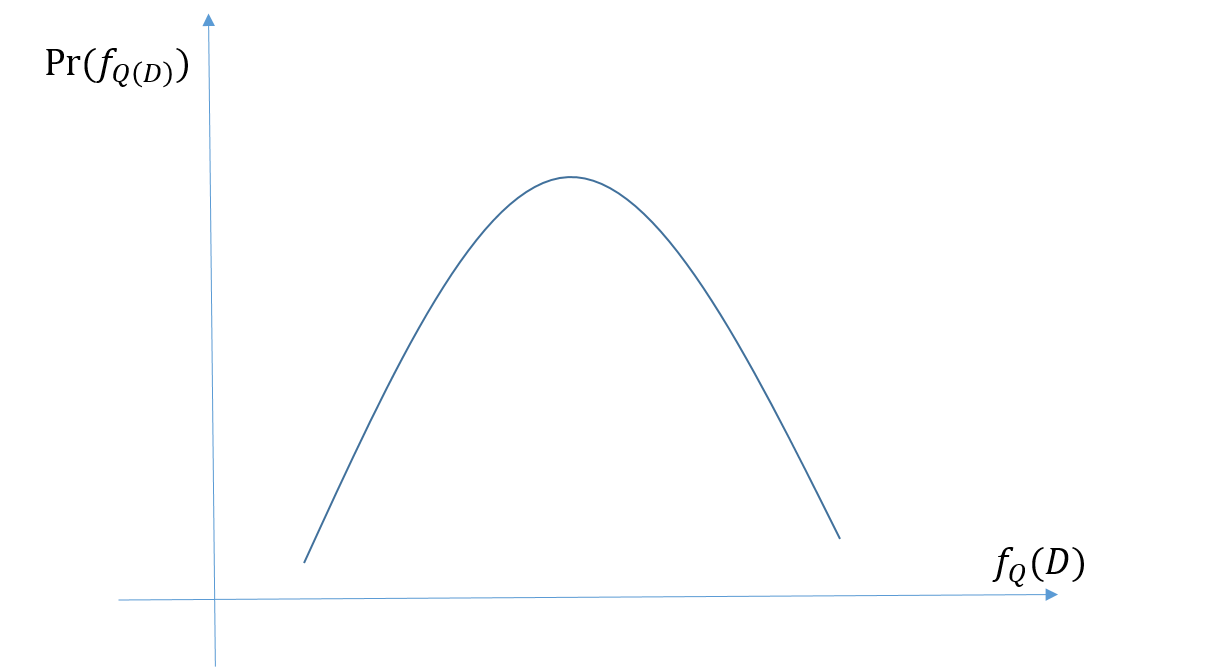
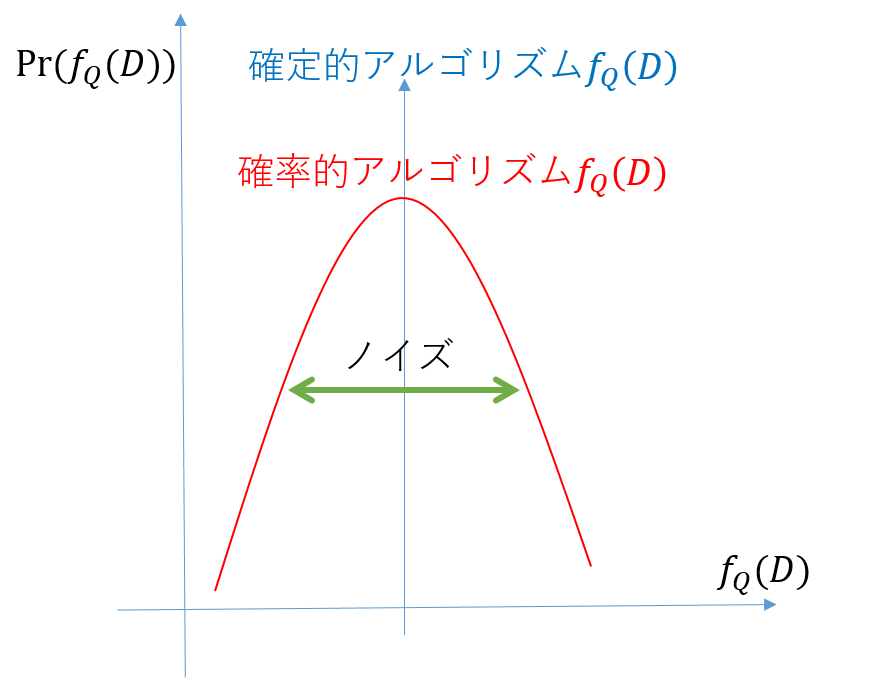
まず、関数 $f_Q$について、この関数はクエリを想定していて、例えば平均値とかです。つまり、引数に与えるデータベースDが同一であれば、必ず同じ値が出力されるので、確定的アルゴリズムだと言えます。しかし、今回はこの関数を確率的アルゴリズムだとみなすこととします。つまり、得られる値にブレが存在します。同じ引数を投げても同じ答えが返ってくるとは限らないってことです。
こうなると話は簡単で、ある値の集合Oを$f_Q$が取る確率が隣接データベースのそれよりも$e^{\epsilon}$倍の範囲に収まっていれば良いわけです。
しかし、実際の関数$f_Q(D)$は確定的アルゴリズムでした。なので、ここまで述べてきたような性質は持ち合わせておらず、どこかの値を100%の確率で取ります。
ここで出てくるのが先に説明したメカニズムなのです。メカニズムは確定的アルゴリズムである$f_Q(D)$をノイズを乗せることで無理やり確率的アルゴリズムに改変します。メカニズムによって、確率的アルゴリズムになった関数$f_Q(D)$は差分プライバシを満たすことができるのです。