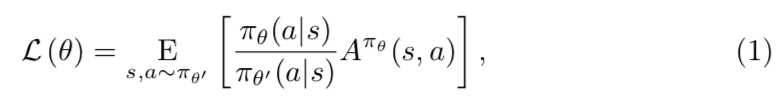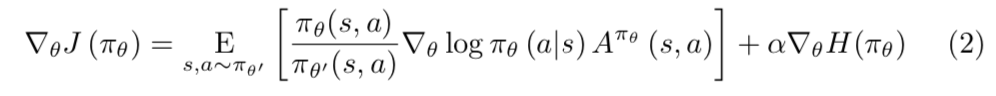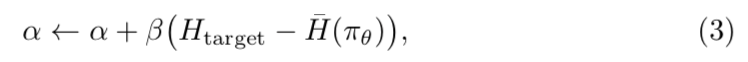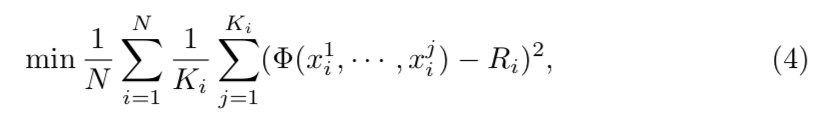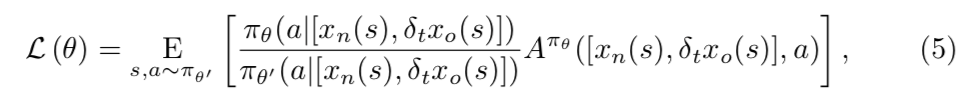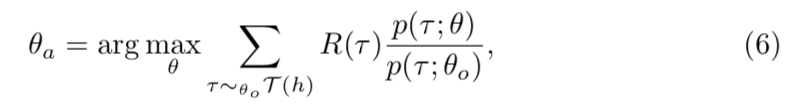こちらの記事の続きになります
この論文を読んだことが無い方はこちらの記事から読むことをおすすめします。
(それと麻雀と情報工学基礎レベル(エントロピッピがわかるレベル)で噛み砕いているので、分かりづらかったらごめんなさい)
3. 学習アルゴリズム
Suphxの学習には大きく3つのステップがあり、天鳳の上位ユーザーの牌譜を用いて5つのモデル(捨て牌・ポン・カン・チー・リーチモデル)を教師あり学習で学習する。次に強化学習によって作成したモデルを改良する。強化学習では3.1節で解説する一般的な勾配アルゴリズムを採用し、3.2節で解説するGlobal reward Predictionと3.3節で解説するOracle guideを導入することで、麻雀特有の課題を解決している。そして最後にオンライン対戦時には3.4節で解説するRuntime Policy adaptation を使用して、現在の局からの予測結果を活用することでよりよい成果を発揮します。
3.1 エントロピー正則化による分散強化学習
Suphxの学習は分散強化学習に基づいており、特に方策勾配法1を採用して、重点サンプリング2を活用することで、非同期分散学習において欲しい範囲のサンプルを重点的にサンプリングすることができる。
$\theta'$ は学習用の軌跡を生成するポリシー3のパラメータである。$\theta$は更新するべき新しいポリシーだが、強化学習ではポリシーのエントロピーに敏感であるため、エントロピーが小さい場合に収束が早まってしまってあまり改善がされない。そのため強化学習中のポリシーのエントロピーを以下のように正則化する。
$H(\pi_{\theta})$ はポリシー $\pi_{\theta}$のエントロピーで、 $\alpha$ はトレードオフ係数にあたる。安定した探索を実施するために、直近でポリシーのエントロピーが $H_{target}$よりも小さいもしくは大きい場合に、エントロピー項を増加もしくは減少するように $\alpha$ を動的に調整する。
$\bar{H}(\pi_{\theta})$ は直近の学習におけるエントロピーであり、$\beta > 0$は小さなステップサイズにあたる。
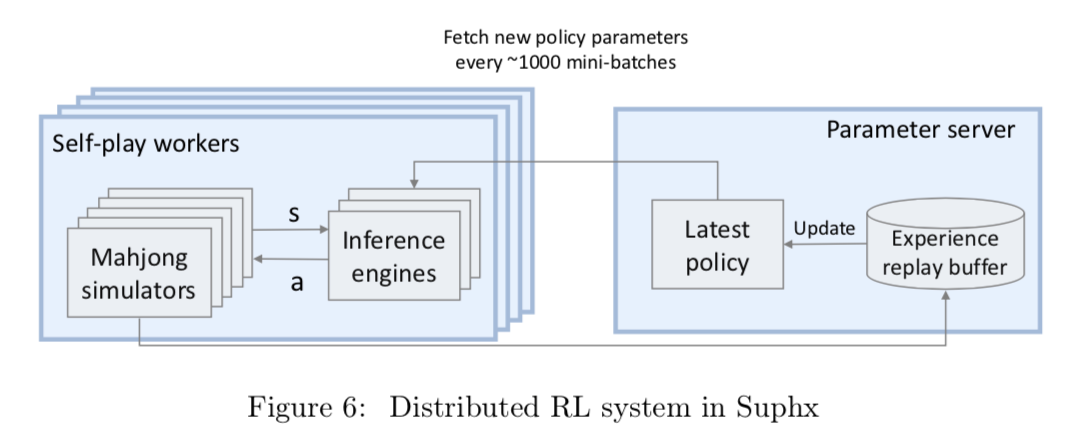
Suphxが使用している分散型強化学習システムを図6に示す。このシステムでは複数のSelf-play workersで構成されていて、それぞれにはCPUベースの麻雀シミュレーターのセットと、軌道を生成するためのGPUベースの推論エンジンのセットが含まれている。ポリシーの更新自体は推論エンジンとは別になっており、Parameter server上にてポリシーを更新する。シミュレーターでは強化学習エージェントをプレイヤーとしてゲームをランダムに実行し、もしアクションを起こす必要があった場合には現在の状況を推論エンジンに送り、行動をエージェントに返す。推論エンジンはParameter serverから最新のポリシーを定期的に更新し最新のポリシーに近いものになるようにしている。
3.2 Global Reward Prediction
麻雀は1半荘で約8局から12局ほど対局するが、プレイヤーは各局終了時に点棒移動が行われオーラス終了時の点数によって最終順位が得られる。しかしこのルールは点棒を軸にしても、現在順位を軸にしても、強化学習という観点では良い報酬になりえない。
- 点棒が報酬になりえない理由として、各局ごとの結果を元にしてうまく打てた局とそうでない局を区別することができない。そのため各局ごとにパフォーマンスを測定する必要がある。
- 現在順位が報酬になりえない理由として、打ち筋が局ごとに異なる(例としてオーラス1着の場合、打ち筋は保守的になるなど)ため、必ずしもアガリを重ね続けることが方針としていいわけではなく、局ごとに打ち方の評価が一定ではないことがあげられる。
したがって、強化学習に効果的な報酬を設計するには、局ごとの理想的な持ち点を各局ごとに適切に与える必要がある。そのために、現在の局と過去の局の情報から、最終的な持ち点を予測するGrobal Reward Prediction $\phi$ を導入する。
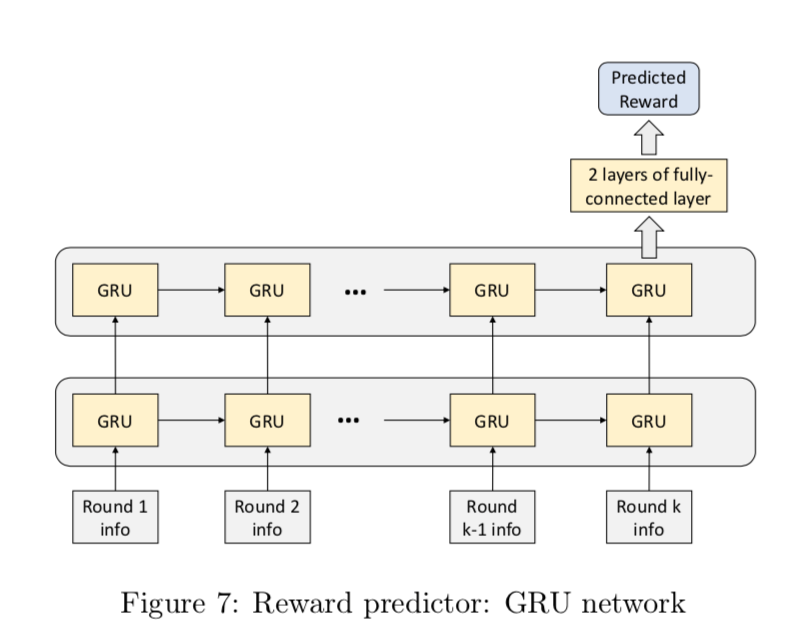
図7に示すように、予測機はRNNで構成され具体的には2層のGRU4とそれに続く2つの全結合層で構成される。予測器の学習データは天鳳の上位プレイヤーの牌譜から来ており、 $\phi$ は平均二乗誤差を最小化することで学習される。
$N$は学習データのゲーム数を差していて、$R_i$はi局時点の持ち点。$K_i$はi局時点の局数、$x^{k}_{i}$はi局時点の特徴ベクトルを示す。 $\phi$ が十分に学習されている場合には、K局のゲームでは強化学習のためにk番目の対局の報酬として $\phi(x^k) - \phi(x^{k-1})$ を使用する。(前の対局より優れた対局ができていたか)
3.3 Oracle Guiding
麻雀には山や王牌や他プレイヤーの手牌など、隠れた情報が多く存在する。これらの情報が見えていない状況で最適な行動を学習するのは難しく、たとえ強化学習で方針を学べるとしても効率はよくなく学習が遅くなることが考えられる。そこで見えていない情報をすべて見える状態のエージェントを導入して学習を高速化する。
隠れ情報を含むすべての情報を得たオラクルエージェントがどのようにして、通常のエージェントの学習を高速化させるのかというと隠れ情報が見える状態を1としたときに、そこから徐々に0に近づけていくようにトレーニングさせることで最終的には通常のエージェントの学習と遜色ない学習にする。0になったときにそこから通常の学習を複数回実施する。この継続的な学習の際に学習率を10分の1にして、重みが予め設定された閾値より大きい場合に、いくつか状態と行動のペアを拒否することで、本稿では安定した学習をみることができた。逆にこれを試さない場合は改善がなかった。
3.4 Prametric Monte-Carlo Policy Adaptation
麻雀の場合、各局ごとに与えられる配牌によって戦略が大きく異なる。例えば手牌が良い場合は点数が大きくなるように積極的に動いたり、悪ければ点数を振り込まないように考えたり点数度外視で早くアガるなどといった風に打っていくだろう。これを事前に戦略として取り入れモデルの予測時に適用させられればより強いエージェントが作成できると考えられる。
モンテカルロ木探索(MCTS)は囲碁や将棋などで使われているものの、初期状態が配牌で異なるためゲームツリーを作るのは難しい。そこで新しくParametric Monte-Carlo Policy Adaptationを提案する。
局が始まる際に事前に学習されたポリシーを初期手牌に対して以下のように適用させる
- シミュレーションの実施
- 具体的には配られた手牌を除いた残りの牌で相手の手牌をランダムにサンプリングして、ポリシーに基づきどのような対局になるかをKパターンほど生成する。
- 適応
- 生成した対局パターンを用いて勾配更新を行って、オフラインポリシーを微調整する
- 推論
- この局で対局するためのポリシーを2で適用させたオフラインポリシーに更新する
$h$ はある局でのエージェントの手牌、 $\theta_o$はオフラインで学習したポリシーのパラメータ、 $\theta_a$ は新しく更新したパラメータになる。 $\tau(h)$ は軌道の集合で、 $p(\tau;\theta)$ はポリシーが軌道を生成する確率になる。
本研究では、シミュレーションの数Kはあまり大きくする必要は鳴くpMCPAは局すべての次の状態を集める必要はない。pMCPAがパラメトリックな手法のため、更新されたポリシーはシミュレーションでは見られなかった状態の推定も更新することができる。つまり、少ないシミュレーションであってもある程度一般化することに役立つ。
ただしポリシーの更新は各局ごとに実施されることに注意する必要がある。その局で更新されたポリシーを次の局で使うことはなく、またオフラインのポリシーをベースに更新していくことになる。
次の目標
アルゴリズムを理解しながらまとめていくの大変だったので4章は次で。