はじめに
研究で深層強化学習を使うことになったので、研究費でゲットした書籍で強化学習を勉強していきます。
筆者はPythonと知識とCNNを勉強して簡単なDeepLearningの知識があります。
強化学習の基本的な用語も知っています。
数式はニガテです。
この書籍では1~6章が強化学習、7~10章で深層強化学習を扱っています。
1章~の知識がある前提で進めていますので、よければご覧ください。
環境
Windows10
Python3系
マルコフ決定過程(MDP)とは
マルコフ決定過程(Markov decision process)は略してMDPともいわれます。
マルコフ決定過程はバラすとマルコフ性の決定過程で、
マルコフ性は後で説明しますが、『状態遷移は「現在の状態」と「現在の行動」だけに依存する』という意味です。
決定過程は『エージェントが「環境」と相互作用しながら「行動」を決定する過程』という意味です。
MDPの具体例
このMDPの例を下の図で示します。
これはエージェントが得点を稼ぐことを目的としています。エージェントは右か左に行動することができます。
図を見たらわかる通り、エージェントが行動するたびに状態が変化しています。
このように、ある時刻でのエージェントの行動によって状態が遷移し、遷移した先で新たに行動するような問題をMDPでは扱います。
そのためMDPには「時間」という概念が必ず存在します。

図の問題ではどちらの行動が良い報酬が得られるでしょうか?
最終的に右のほうが良い報酬が得られていますね。MDPでは目先の報酬(罰)で判断せず、将来的な報酬の総和を考える必要があります。
エージェントと環境は次のようなやりとりを行って遷移をしています。
$$ s_0, a_0, r_0, s_1, a_1, r_1,s_2, a_2, r_2, \cdots$$
これは初期状態が$s_0$です。言葉で表現すれば、状態$s_0$でエージェントが行動$a_0$を行い報酬$r_0$を得て、時刻が進み、状態$s_1$でエージェントが行動$a_1$を行い報酬$r_1$を得て、次の状態$s_2$へ・・・という遷移です。
以上がMDPの概要となります。
環境とエージェントのやりとりの数式化
MDPを解くために、環境とエージェントのやりとりの以下の3つの要素を数式化します。
- 状態遷移:状態はどのように遷移するか
- 方策:エージェントはどのように行動するか
- 報酬:報酬はどのように与えられるか
状態遷移の数式化
状態遷移:状態はどのように遷移するか
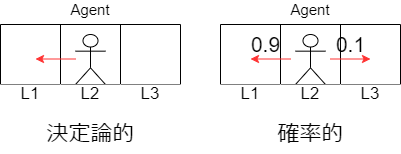
状態遷移の図を下に示します。

どちらも最初エージェントは状態$L2$で行動$Left$を選択しています。
左図では必ず左の状態$L1$に遷移しています。このような性質を決定論的といいます。
状態遷移が決定論的である場合、次の状態$s'$は現在の状態$s$と行動$a$によって一意に定まるので、数式は次のように表すことができます。
$$s'=f(s, a)$$
この$f(s, a)$を状態遷移関数といいます。
右図では左の行動を選択していますが、何らかの要因によって確率0.1で止まってしまうことがあります。要因は何でもよく、小石でつまずいてしまったり、四方にいきなり壁が出現したとかで、行動を阻害された場合止まってしまいます。
このように確率で決まるような性質を確率的といい、数式は次の王に表すことができます。
$$p(s'|s, a)$$
この$p(s'|s, a)$を状態遷移確率といいます。状態遷移確率の中身は上の図の問題の場合、次の表のようになっています。
| s' | L1 | L2 | L3 |
|---|---|---|---|
| $p(s'|s=L2, a=Left)$ | 0.9 | 0.1 | 0.0 |
マルコフ性
以上から分かるように、状態遷移確率$p(s'|s, a)$は現在の状態$s$と現在の行動$a$のみから決定されます。
言い換えれば、次の状態を決めるために、過去の行動や、過去の状態の変化は必要ないということです。
このことをマルコフ性といいます。
マルコフ性を導入する理由は、問題を解きやすくするためです。過去全ての行動や状態を考慮すると組み合わせが指数関数的に増加してしまいます。
方策の数式化
方策:エージェントがどのように行動するか
エージェントの方策はマルコフ性によって、現在の状態からのみ決定されます。
状態遷移と少し似ていますが、状態遷移は行動した後の「状態」を表し、方策はエージェントが選択する「行動」を表しています。
決定論的な方策の場合、行動は一意に定まり次の式で表します。
$$ a= \mu(s) $$
確率的な方策の場合、行動は確率的で次の式で表します。
$$\pi(a|s)$$
| Action | Left | Right |
|---|---|---|
| $\pi(a|L1) $ | 0 | 1.0 |
| $\pi(a|L2) $ | 0.9 | 0.1 |
| $\pi(a|L3) $ | 1.0 | 0 |
上の図の問題の場合$\pi(a|s)$中身はこの表のようになっています。
報酬の数式化
報酬:報酬はどのように与えられるか
報酬も決定論的に与えられる場合もあれば、確率的に与えられる場合もあります。
この書籍にでは簡単のために報酬は決定論的の場合のみを扱います。
決定論的に与えられる報酬を次の数式で表します。
$$ r(s,a,s')$$
ちなみに確率論的に報酬が与えられる場合は、報酬が得られる期待値を使います。
MDPの目標
ここまでで環境とエージェントのやり取りを数式化することができました。
MDPの目標は、定式化したMDPを使って最適方策を見つけることです。
そのためにMDPの問題を大きく2つに分けます。
- エピソードタスク:囲碁などのように「始まり」と「終わり」があるタスク
- 連続タスク:在庫管理などのように終わりがないタスク
収益を導入
ここで収益という用語を導入します。この収益を最大化することがエージェントの目標です。
収益を定義するにあたり前提として、時刻$t$で環境$s_t$、行動$a_t$をしたとき、報酬$r_t$を得て、$s_{t+1}$に遷移するときの収益を$G_t$とします。
そして$G_t$は次のように定義されます。
$$G_t=R_t+\gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots $$
定義のとおり、収益はエージェントが得る報酬の総和で表されます。ただし $\gamma$ によって後ろの時間になればなるほど報酬が減衰されます。この $\gamma$ は割引率と呼ばれ、$0.0<\gamma<1.0$で設定されます。
割引率を設定する理由は主に
- 連続タスクの時、報酬が無限大になることを防ぐ
- 近い報酬ほど重要に見せかける
(10年後の2万円と1年後の1万円であれば、1年後の方をとりますよね!)
状態価値関数
「収益」を導入しましたが、方策や状態遷移が確率的にふるまう場合、収益も確率的に変化します。
このとき、収益の期待値を指標とし、数式を次のように表します。
$$ v_\pi(s)=E[G_t|S_t=s,\pi] $$
これは状態$S_t$が$s$で、エージェントの方策が$\pi$であることを条件としてあたえられます。
そして$ v_\pi(s) $を状態価値関数と呼ばれます。
状態価値関数の比較
ある問題の方策が$\pi_1$,$\pi_2$の2つあるとします。それぞれすべての状態で状態価値関数$ v_\pi(s) $が以下のグラフのように決まったと仮定します。

このグラフでは$\pi_1$, $\pi_2$のどちらが優れた方策といえるでしょうか。
この場合、どちらも優劣をつけることはできません。
次に、下のグラフのように別の状態価値関数が決まったとします。

このグラフではすべての状態で$\pi_2$の状態価値関数が$\pi_1$の状態価値関数を上回っているか等しい値にありますす。
この場合$\pi_2$は$\pi_1$より優れているといえます。
全ての状態でどの方策の状態価値関数の値より優れている方策を最適方策といいます。
MDPには必ず最適方策が1つは存在し、その方策は必ず決定論的方策となっています。これを$a=\mu_*(s)$で表します。最適方策の状態関数を最適状態関数といいます。
MDPの最適化
今まで私たちは
- MDPを定式化するために、エージェントと環境のやり取りの数式化
- 最適化の目標をさだめるために、収益、状態価値関数の導入
- 方策の優劣をつけるために、状態価値関数の比較
を行ってきました。
この流れを行うことでMDPの最適方策を見つけることができます。
具体例は気が向いたら書くことにします。
おわりに
最後までお読みいただきありがとうございます。
勉強しながらちょこちょこ書いていきますのでよろしくお願いします。