はじめに
FA(ファクトリーオートメーション)の現場やマシンビジョンにおけるステージやテーブルの位置決め制御では、ステッピングモータとサーボモータが広く使われています。
「どちらを使えばよいのか?」という疑問は、装置設計で必ず直面する課題です。本記事では、両モータの動作原理から制御方式、駆動方式、台形駆動による移動距離の計算まで、体系的に解説します。
本記事の対象読者:
- モータ制御をこれから学ぶ方
- ステッピングモータとサーボモータの使い分けを整理したい方
- マシンビジョンのステージ制御でモータを選定する必要がある方
1. ステッピングモータとは
1.1 動作原理
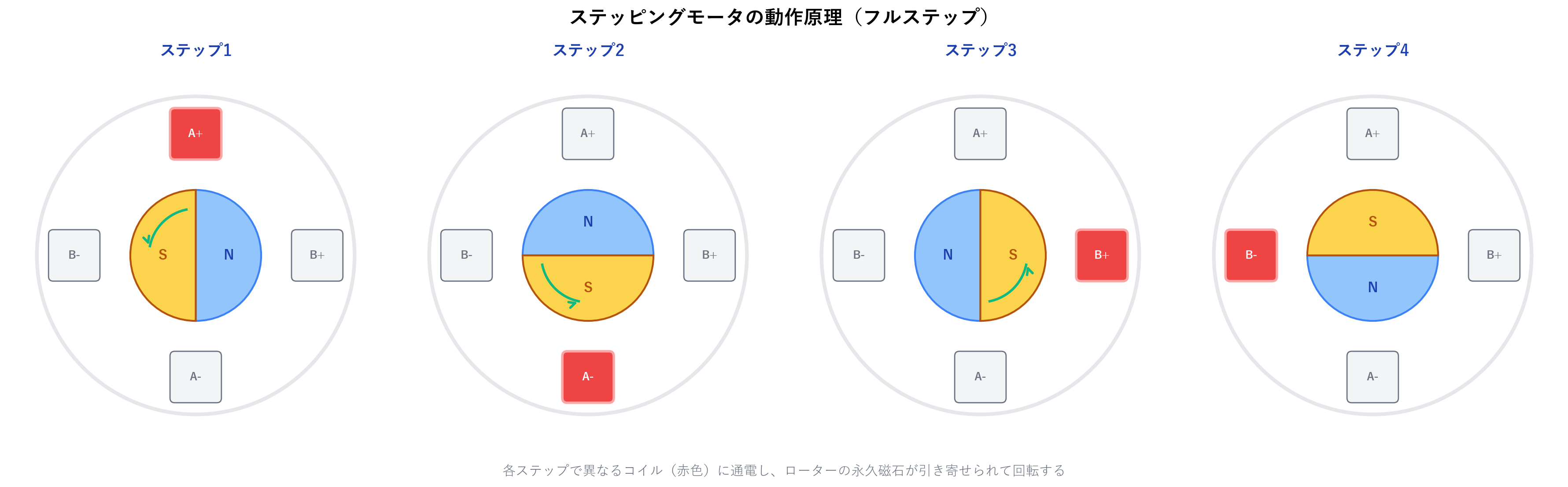
ステッピングモータは、パルス信号を入力するたびにローターが一定角度(ステップ角)だけ回転するモータです。
構造としては、永久磁石のローター(回転子)の周囲に、複数の電磁コイル(ステーター)が配置されています。各コイルに順番に電流を流すことで磁界が切り替わり、ローターが段階的に回転します。
ステッピングモータの基本特性:
- パルス数で回転角度が決まる → 位置制御が容易
- パルス周波数で回転速度が決まる → 速度制御が容易
- 通電状態で停止トルク(ホールディングトルク)を発生 → 停止時の保持力がある
- 構造がシンプルでブラシレス → 長寿命・メンテナンスフリー
1.2 2相ステッピングモータと5相ステッピングモータ
FA分野で広く使われるステッピングモータは、主に2相と5相の2種類があります。相数の違いは、ステップ角・分解能・振動特性に大きく影響します。
| 項目 | 2相ステッピングモータ | 5相ステッピングモータ |
|---|---|---|
| ステップ角(フルステップ) | 1.8° | 0.72° |
| 1回転あたりのパルス数(フルステップ) | 200 pulse/rev | 500 pulse/rev |
| 1回転あたりのパルス数(ハーフステップ) | 400 pulse/rev | 1,000 pulse/rev |
| 1回転あたりのパルス数(1/16マイクロステップ) | 3,200 pulse/rev | 8,000 pulse/rev |
| 振動 | やや大きい | 小さい(滑らかな回転) |
| トルクリップル | 大きい | 小さい |
| コスト | 安い | やや高い |
| ドライバ | 汎用品が豊富 | 5相専用ドライバが必要 |
2相ステッピングモータ
最も普及しているタイプです。A相・B相の2つの相で構成され、フルステップ角は 1.8°(1回転 = 200パルス)です。
- メリット:低コスト、ドライバの選択肢が豊富、入手性が良い
- デメリット:振動がやや大きい、低速回転時の振動が顕著
- 用途:コスト重視の一般的な位置決め、3Dプリンタ、簡易ステージ
5相ステッピングモータ
5つの相で構成され、フルステップ角は 0.72°(1回転 = 500パルス)です。2相と比較して 2.5倍の分解能 を持ちます。
- メリット:高分解能、低振動、滑らかな回転、トルクリップルが小さい
- デメリット:2相より高コスト、5相専用ドライバが必要
- 用途:マシンビジョンのステージ制御、精密位置決め、半導体製造装置
5相モータは相数が多い分、ローターの停止位置が細かく刻まれるため、フルステップでも2相のハーフステップ以上の分解能があります。マシンビジョンのステージ制御のように低振動・高分解能が求められる用途では、5相モータが好まれます。
1.3 ステップ駆動の種類
ステッピングモータの分解能(1ステップあたりの回転角度)は、駆動方式によって変わります。
フルステップ駆動
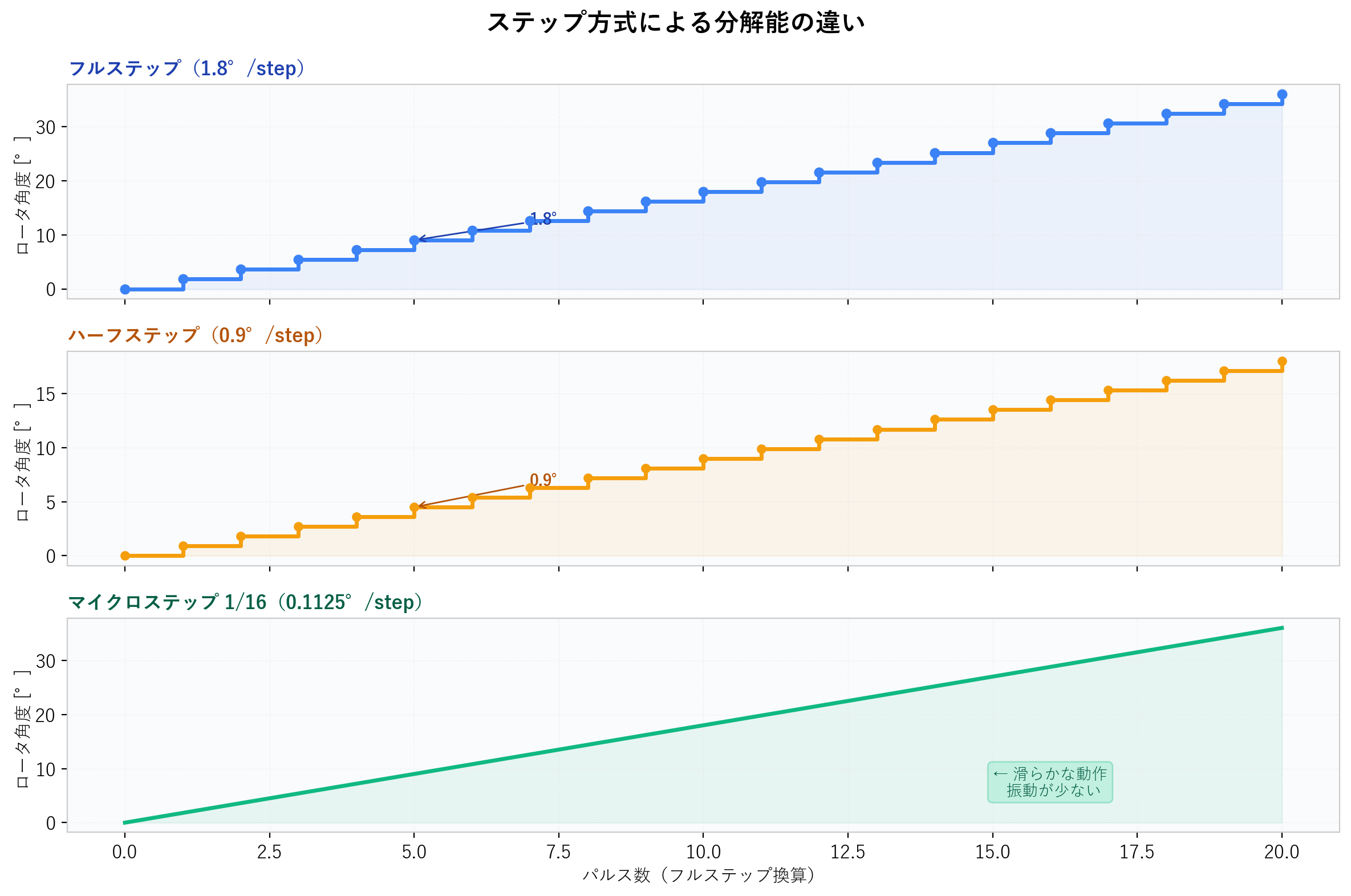
最も基本的な駆動方式です。1パルスあたりステップ角(例:1.8°)だけ回転します。
- 分解能:1.8°/step(200 step/rev)
- 特徴:トルクが最大、制御がシンプル
- 欠点:振動が大きい、動作音が大きい
フルステップでは、常に1つの相(または2つの相)に電流を流し、ステーターの磁界を大きく切り替えます。この離散的な切り替えが振動の原因となります。
ハーフステップ駆動
フルステップの中間位置にも停止できるようにした駆動方式です。1パルスあたり 0.9° 回転します。
- 分解能:0.9°/step(400 step/rev)
- 特徴:フルステップより振動が少ない
- 仕組み:1相励磁と2相励磁を交互に行うことで、中間角度の位置を実現
マイクロステップ駆動
各相に流す電流を正弦波状に細かく制御することで、フルステップをさらに細分化する方式です。
- 分解能:1/4, 1/8, 1/16, 1/32, 1/64 ... と設定可能
- 例:1/16 マイクロステップの場合 → 0.1125°/step(3,200 step/rev)
- 特徴:非常に滑らかな動作、振動・騒音が大幅に低減
- 注意点:マイクロステップを細かくするほど 1ステップあたりのトルクは低下する
マイクロステップは分解能を向上させますが、位置決め精度がそのまま向上するわけではありません。トルクの低下や負荷条件によっては、理論上の分解能通りの精度が出ない場合があります。
1.3 脱調(ステップアウト)
ステッピングモータ特有の重要な問題が脱調です。
脱調とは、モータに与えたパルス数と実際のローター回転角度がずれてしまう現象です。以下の場合に発生します:
- 負荷トルクがモータの出力トルクを超えた場合
- 急激な加減速でローターが磁界の変化に追従できない場合
- 高速回転時にトルクが不足した場合
脱調が発生すると、コントローラ側はパルスを出し続けているためズレに気づけません。これがオープンループ制御の最大の弱点です。
脱調対策:
- トルクに余裕を持ったモータ選定(安全率 2倍以上)
- 適切な加減速プロファイルの設定(台形駆動・S字駆動)
- 脱調検知機能付きドライバの使用
- クローズドループ化(エンコーダ追加)
2. サーボモータとは
2.1 動作原理
サーボモータは、エンコーダによる位置・速度フィードバックを用いて、目標位置に正確に追従させるモータです。
一般的にFA分野で「サーボモータ」と呼ばれるのは、ACサーボモータ(永久磁石同期モータ:PMSM) です。ステッピングモータと同様にブラシレス構造ですが、制御方式が根本的に異なります。
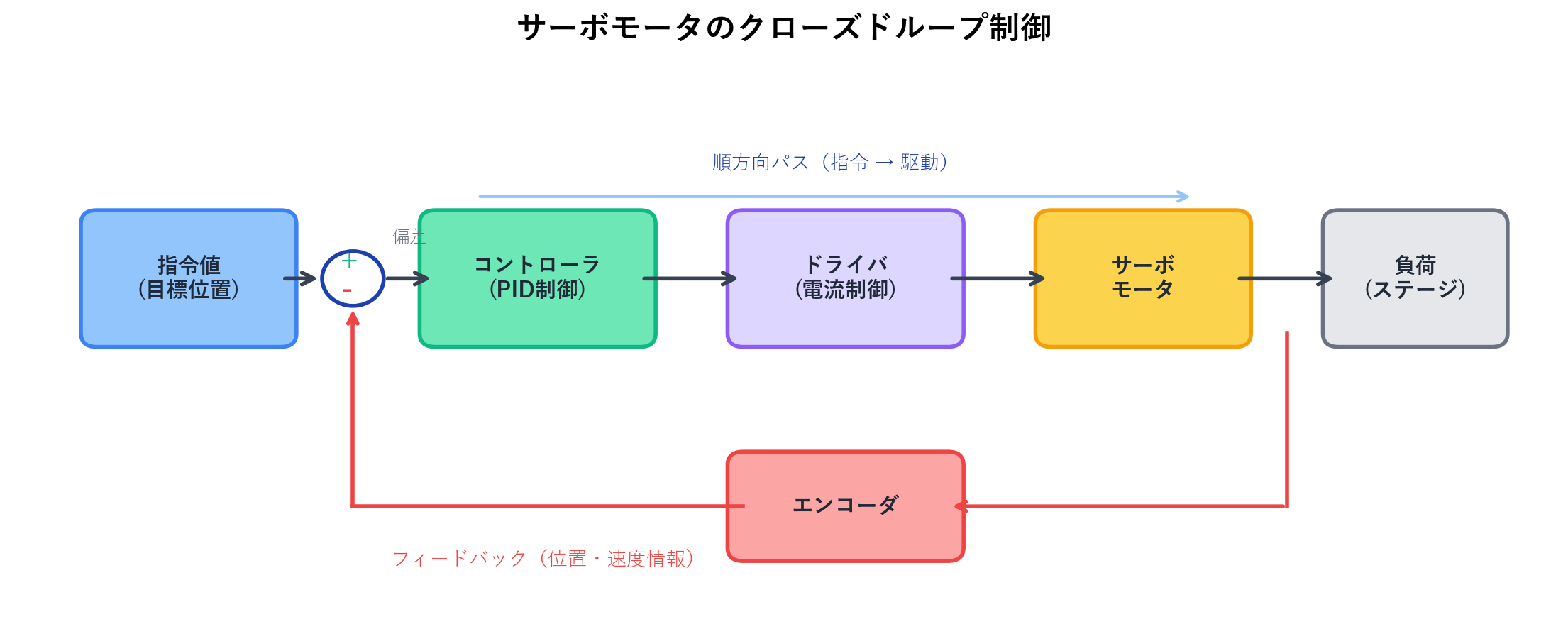
サーボモータの動作は以下の流れで行われます:
- コントローラが**目標位置(指令値)**を出す
- ドライバがモータに電流を供給し、回転させる
- エンコーダが現在位置をリアルタイムに検出する
- 目標位置と現在位置の**偏差(誤差)**を計算する
- 偏差をゼロにするようにドライバが電流を調整する
この一連の流れが**クローズドループ制御(フィードバック制御)**です。
2.2 エンコーダの役割
エンコーダは、モータの回転角度や回転速度を検出するセンサーです。サーボモータの心臓部とも言えます。
| 種類 | 分解能 | 特徴 |
|---|---|---|
| インクリメンタルエンコーダ | 数百〜数百万 パルス/回転 | 相対位置を検出。電源ON時に原点復帰が必要 |
| アブソリュートエンコーダ | 数万〜数百万 分解能/回転 | 絶対位置を検出。電源ON時にすぐ位置が分かる |
マシンビジョンのステージ制御では、17bit(131,072分解能)以上のアブソリュートエンコーダが一般的に使用されます。これにより、1回転あたり 0.0027°以下の分解能が得られます。
2.3 振動とハンチング
サーボモータはクローズドループ制御の高精度さと引き換えに、振動やハンチングの問題が生じることがあります。
振動
サーボモータの振動は、主に以下の原因で発生します:
- ゲイン設定が高すぎる:応答性を上げるためにPIDゲインを高く設定すると、オーバーシュートが発生し、目標位置付近で振動する
- 機械系の共振:モータの制御周波数と機械系の固有振動数が一致すると共振が発生する
- バックラッシュ:ギアやカップリングの遊びにより、位置制御が不安定になる
ハンチング
ハンチングとは、目標位置付近で微小な往復運動を繰り返す現象です。サーボモータが目標位置に到達しようとして行き過ぎ(オーバーシュート)、戻りすぎ(アンダーシュート)を繰り返す状態です。
ハンチングの主な原因:
- PIDゲイン(特に比例ゲインと微分ゲイン)の不適切な設定
- 機械系の摩擦特性(静止摩擦と動摩擦の差が大きい場合)
- フィードバック系の遅延
ハンチング対策:
- PIDゲインの適切な調整(オートチューニング機能の活用)
- 位置決め完了判定の不感帯(インポジション幅)の適切な設定
- 機械系の剛性向上
- フィードフォワード制御の併用
ハンチングは「位置決め完了」の判定にも影響します。エンコーダが高分解能であるほど微小な振動も検出してしまうため、インポジション幅(位置決め完了とみなす許容偏差)の設定が重要です。
3. 制御方式の比較:オープンループ vs クローズドループ
3.1 オープンループ制御(ステッピングモータ)
指令パルス → ドライバ → モータ → 負荷
(フィードバックなし)
特徴:
- パルス数 = 移動量として制御(エンコーダ不要)
- 制御系がシンプル・低コスト
- 脱調が発生してもコントローラが検知できない
- 高負荷・高速域で信頼性が低下
適している用途:
- 負荷条件が安定している
- 高精度が不要(数μm〜数十μm程度)
- コストを抑えたい
- シンプルな制御で済ませたい
3.2 クローズドループ制御(サーボモータ)
指令値 → コントローラ → ドライバ → モータ → 負荷
↑ ↓
└──── エンコーダ ←──────────┘
(フィードバック)
特徴:
- リアルタイムに位置・速度を監視し、偏差を補正
- 外乱(負荷変動・摩擦など)に対して自動補正が可能
- 脱調の概念がない(常にフィードバックで追従)
- PIDゲイン調整が必要
適している用途:
- 高精度な位置決めが必要(サブμmレベル)
- 負荷条件が変動する
- 高速・高加速度が必要
- 信頼性の高い制御が求められる
4. ステッピングモータとサーボモータの徹底比較
4.1 比較一覧表
| 比較項目 | ステッピングモータ | サーボモータ |
|---|---|---|
| 制御方式 | オープンループ | クローズドループ |
| 位置検出 | なし(パルス数で管理) | エンコーダ |
| 位置決め精度 | ±数十μm〜±数μm | ±数μm〜±サブμm |
| 繰り返し精度 | ±数μm〜±数十μm | ±サブμm |
| 最高回転速度 | 〜1,000 rpm程度 | 〜6,000 rpm以上 |
| トルク特性 | 低速で高トルク、高速で急低下 | 全速度域で安定したトルク |
| 脱調リスク | あり | なし |
| 振動・騒音 | やや大きい(特にフルステップ) | 小さい |
| ハンチング | 発生しない※ | 調整不良時に発生 |
| 応答性 | 低い(オープンループのため) | 高い |
| コスト(モータ単体) | 安い | 高い |
| コスト(システム全体) | 安い(エンコーダ不要) | 高い(エンコーダ・ドライバ込み) |
| 制御の複雑さ | シンプル | 複雑(PID調整が必要) |
| 保持力(無通電時) | ディテントトルクあり | なし(ブレーキが必要な場合あり) |
※ ステッピングモータは位置フィードバックがないため、ハンチング(目標位置付近での振動的な追従動作)は発生しません。ただし、ステップ駆動に起因する振動は存在します。
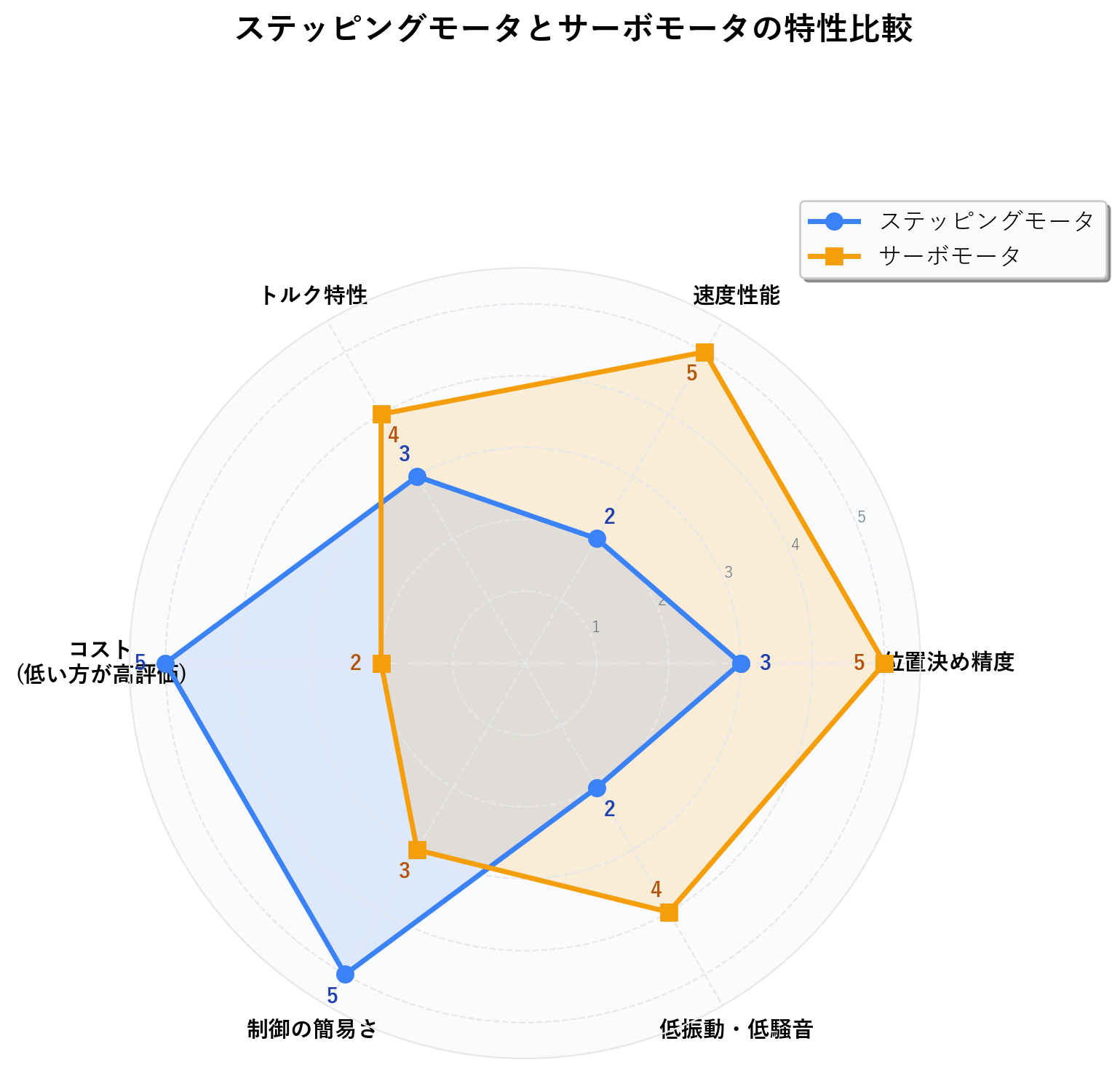
4.2 特性レーダーチャート
4.3 位置決め精度の比較
マシンビジョンにおけるステージ制御では、位置決め精度が最も重要な要素です。
ステッピングモータの位置決め精度
ステッピングモータの位置精度は、以下の要素で決まります:
$$
\text{位置精度} = \text{ステップ角精度} \pm \text{分割精度} \pm \text{機械系誤差}
$$
- ステップ角精度:一般的に ±3〜5%(非累積誤差)
- マイクロステップ分割精度:理論値からのずれ
- フルステップ 1.8° の場合:1回転 = 200 step → 直動ステージ(リード 2mm)で 10μm/step
- 1/16 マイクロステップの場合:1回転 = 3,200 step → 0.625μm/step
サーボモータの位置決め精度
サーボモータの位置精度は、エンコーダの分解能とサーボ系の追従性能で決まります:
$$
\text{位置精度} \approx \text{エンコーダ分解能} + \text{サーボ偏差} + \text{機械系誤差}
$$
- エンコーダ分解能:17bit(131,072 パルス/回転)の場合、直動ステージ(リード 2mm)で 0.015μm/pulse
- サーボ偏差:PIDゲインとフィードバック周期に依存
結論:位置決め精度を最優先するならサーボモータが有利です。ただし、±数μm程度の精度であれば、マイクロステップ駆動のステッピングモータでも十分対応できるケースがあります。
4.4 コスト vs 性能
モータ選定はコストと性能のトレードオフです。以下に目安を示します。
| 要求精度 | 推奨モータ | コスト感 |
|---|---|---|
| ±100μm 以上 | ステッピングモータ(フルステップ) | ★☆☆☆☆ |
| ±10〜100μm | ステッピングモータ(マイクロステップ) | ★★☆☆☆ |
| ±1〜10μm | ステッピングモータ(マイクロステップ)or サーボモータ | ★★★☆☆ |
| ±1μm 以下 | サーボモータ | ★★★★☆ |
| ±0.1μm 以下 | サーボモータ+リニアスケール | ★★★★★ |
コスト比較の目安(同等出力クラス):
| 構成 | 相対コスト |
|---|---|
| ステッピングモータ + ドライバ | 1.0x(基準) |
| ステッピングモータ + ドライバ + エンコーダ(クローズドループ化) | 1.5〜2.0x |
| サーボモータ + ドライバ(エンコーダ一体型) | 2.5〜4.0x |
5. モータの制御:台形駆動
モータを「いきなり最高速度で動かし、いきなり停止する」ことは、物理的に不可能であり、脱調や機械への衝撃の原因となります。そこで、速度を滑らかに変化させる加減速制御が必要です。
最も広く使われるのが**台形駆動(台形加減速制御)**です。
5.1 台形駆動とは
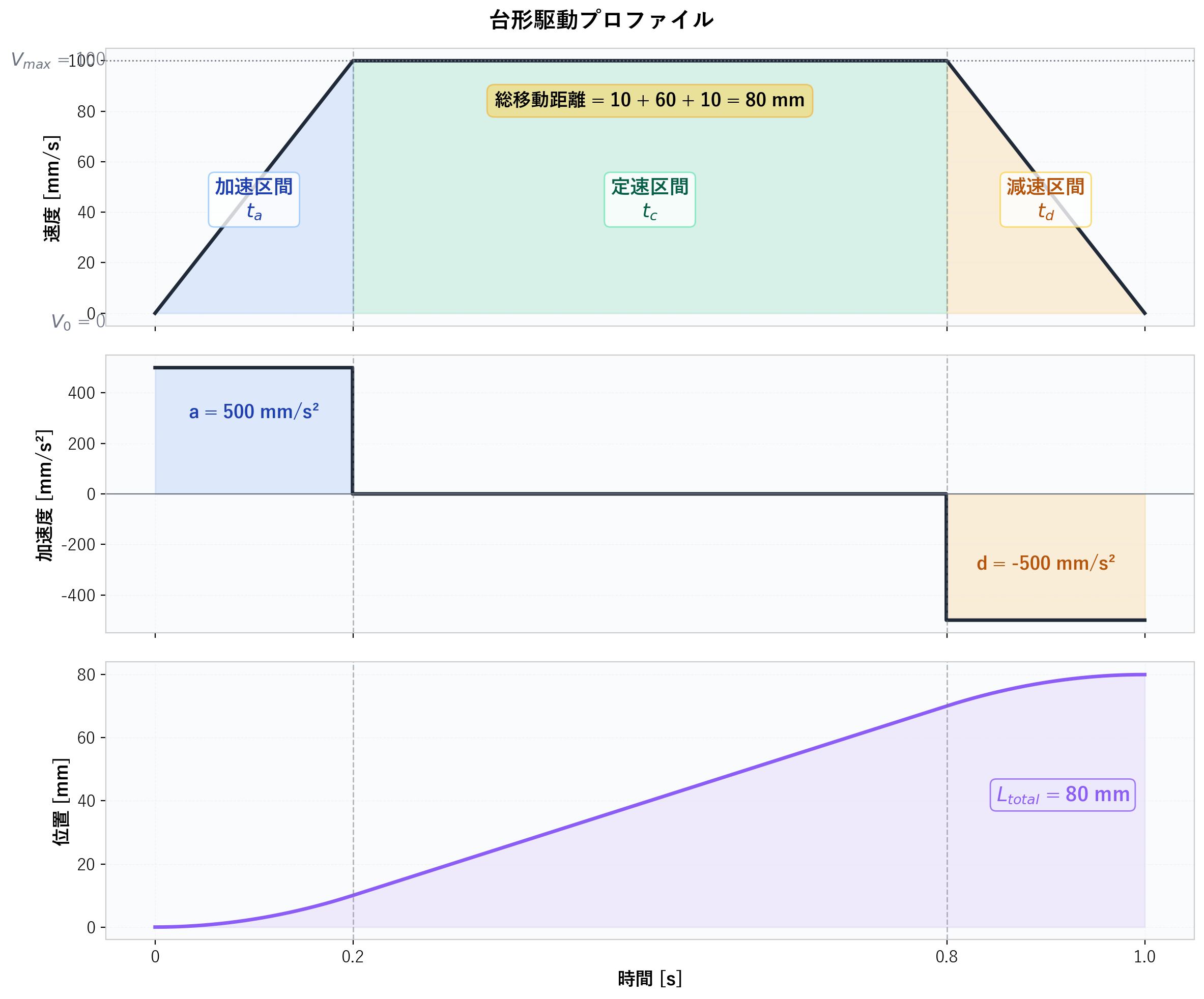
台形駆動は、速度プロファイルが台形の形状をしている加減速制御方式です。
台形駆動は以下の 3つの区間 で構成されます:
| 区間 | 名称 | 動作 |
|---|---|---|
| 第1区間 | 加速区間 | 初速 $V_0$ から最高速度 $V_{max}$ まで一定の加速度で加速 |
| 第2区間 | 定速区間 | 最高速度 $V_{max}$ を維持して等速運動 |
| 第3区間 | 減速区間 | 最高速度 $V_{max}$ から停止(または目標速度)まで一定の減速度で減速 |
5.2 台形駆動のパラメータ設定
台形駆動で設定するパラメータは以下の通りです:
| パラメータ | 記号 | 単位 | 説明 |
|---|---|---|---|
| 初速 | $V_0$ | mm/s | 運動開始時の速度(通常は0) |
| 最高速度 | $V_{max}$ | mm/s | 定速区間の速度 |
| 加速時間 | $t_a$ | s | 初速から最高速度に達するまでの時間 |
| 減速時間 | $t_d$ | s | 最高速度から停止するまでの時間 |
| 加速度 | $a$ | mm/s² | $a = \frac{V_{max} - V_0}{t_a}$ |
| 減速度 | $d$ | mm/s² | $d = \frac{V_{max} - V_0}{t_d}$ |
加速度の設定は慎重に行う必要があります。
- ステッピングモータ:加速度が大きすぎると脱調を起こします
- サーボモータ:加速度が大きすぎるとオーバーシュートや機械への衝撃が発生します
5.3 移動距離の計算方法
台形駆動における移動距離は、速度-時間グラフの面積として求められます。
基本の計算式
各区間の移動距離を計算し、合計します。
■ 加速区間の移動距離 $L_a$
加速区間は初速 $V_0$ から最高速度 $V_{max}$ まで等加速度運動をするので、速度-時間グラフでは台形(初速が0の場合は三角形)になります。
$$
L_a = \frac{(V_0 + V_{max})}{2} \times t_a
$$
■ 定速区間の移動距離 $L_c$
定速区間は最高速度 $V_{max}$ で等速運動をするので、長方形の面積です。
$$
L_c = V_{max} \times t_c
$$
ここで $t_c$ は定速区間の時間です。
■ 減速区間の移動距離 $L_d$
減速区間は最高速度 $V_{max}$ から停止するまでの台形(三角形)です。
$$
L_d = \frac{V_{max}}{2} \times t_d
$$
(停止速度が0の場合)
■ 総移動距離 $L_{total}$
$$
\boxed{L_{total} = L_a + L_c + L_d = \frac{(V_0 + V_{max})}{2} \times t_a + V_{max} \times t_c + \frac{V_{max}}{2} \times t_d}
$$
計算例
以下の条件で移動距離を計算します:
| パラメータ | 値 |
|---|---|
| 初速 $V_0$ | 0 mm/s |
| 最高速度 $V_{max}$ | 100 mm/s |
| 加速時間 $t_a$ | 0.2 s |
| 定速時間 $t_c$ | 0.6 s |
| 減速時間 $t_d$ | 0.2 s |
ステップ1:加速度の確認
$$
a = \frac{V_{max} - V_0}{t_a} = \frac{100 - 0}{0.2} = 500 \text{ mm/s}^2
$$
ステップ2:各区間の移動距離
$$
L_a = \frac{(0 + 100)}{2} \times 0.2 = 10 \text{ mm}
$$
$$
L_c = 100 \times 0.6 = 60 \text{ mm}
$$
$$
L_d = \frac{100}{2} \times 0.2 = 10 \text{ mm}
$$
ステップ3:総移動距離
$$
L_{total} = 10 + 60 + 10 = 80 \text{ mm}
$$
ステップ4:全体の所要時間
$$
T_{total} = t_a + t_c + t_d = 0.2 + 0.6 + 0.2 = 1.0 \text{ s}
$$
逆算:定速時間の求め方
実務では、「総移動距離が決まっていて、定速時間を求める」ケースが多いです。
$$
t_c = \frac{L_{total} - L_a - L_d}{V_{max}}
$$
例えば、総移動距離 150mm、その他の条件が同じ場合:
$$
t_c = \frac{150 - 10 - 10}{100} = 1.3 \text{ s}
$$
$$
T_{total} = 0.2 + 1.3 + 0.2 = 1.7 \text{ s}
$$
三角駆動(台形にならない場合)
移動距離が短い場合、定速区間がなく三角形の速度プロファイルになることがあります。これは、加速区間と減速区間だけで目標距離に到達する場合です。
三角駆動の条件:
$$
L_{total} < L_a + L_d = \frac{(V_0 + V_{max})}{2} \times t_a + \frac{V_{max}}{2} \times t_d
$$
この場合、最高速度 $V_{max}$ に到達する前に減速を開始する必要があります。実際に到達する最高速度 $V_{peak}$ は以下で求められます:
$$
V_{peak} = \sqrt{\frac{2 \cdot a \cdot d \cdot L_{total}}{a + d} + V_0^2 \cdot \frac{d}{a+d}}
$$
$V_0 = 0$、$a = d$ の場合(加減速度が等しく、初速が0)は簡略化できます:
$$
V_{peak} = \sqrt{a \cdot L_{total}}
$$
6. 参考:S字駆動
6.1 S字駆動とは
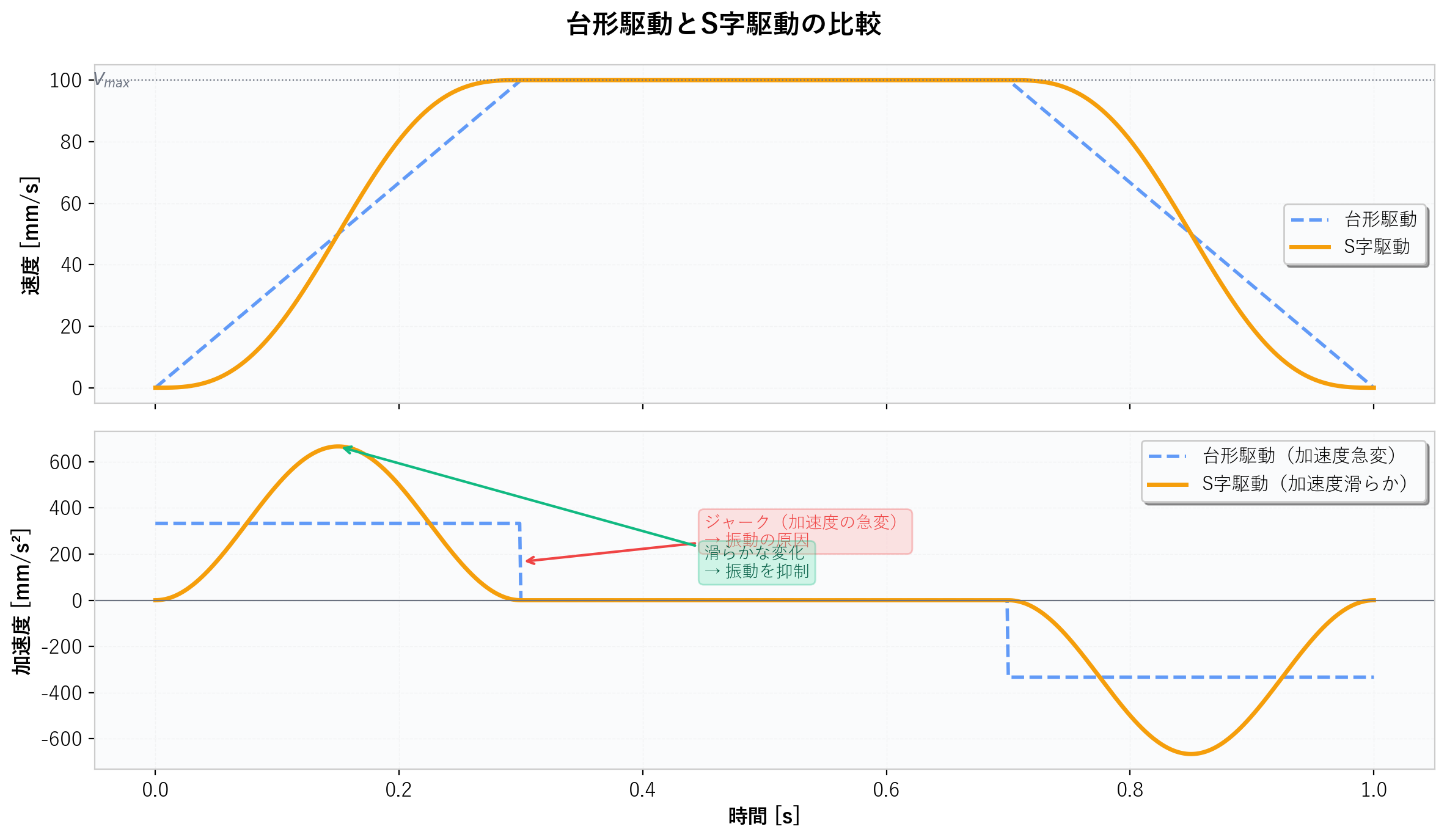
台形駆動では加速度がステップ状に変化するため、加速開始時と加速終了時に**加速度の急変(ジャーク)**が発生します。このジャークが機械振動の原因となります。
S字駆動(S字加減速制御)は、加速度を滑らかに変化させることで、ジャークを抑制する制御方式です。
6.2 台形駆動とS字駆動の違い
| 項目 | 台形駆動 | S字駆動 |
|---|---|---|
| 加速度の変化 | ステップ状(急変) | 滑らかに変化 |
| ジャーク(加加速度) | 無限大(理論上) | 有限値に制限 |
| 振動 | やや大きい | 小さい |
| 整定時間 | 短い場合もある | やや長くなる場合がある |
| 実装の複雑さ | シンプル | やや複雑 |
| 適用場面 | 一般的な位置決め | 高精度・低振動が必要な場面 |
S字駆動は「加速度が台形」の形状をしています。台形駆動は「速度が台形」ですが、S字駆動は「加速度が台形」であるため、速度プロファイルはS字状の滑らかなカーブになります。マシンビジョンにおける高精度なステージ制御では、振動を抑制するためにS字駆動が好まれるケースがあります。
7. マシンビジョンにおけるモータ選定の指針
最後に、マシンビジョンのステージ・テーブル制御におけるモータ選定の指針をまとめます。
ステッピングモータを選ぶべき場面
- 要求精度が ±数μm〜±数十μm 程度で十分な場合
- 負荷条件が一定で脱調のリスクが低い場合
- コストを抑えたい場合
- 制御システムをシンプルに保ちたい場合
- カメラの撮像位置を切り替えるなど、パターン化された動作が中心の場合
サーボモータを選ぶべき場面
- 要求精度が ±1μm 以下の高精度が必要な場合
- 高速な位置決め(タクトタイム短縮)が求められる場合
- 負荷が変動する可能性がある場合
- 連続運転で信頼性が重要な場合
- 追従制御や、動きながら撮像するような用途
選定フローチャート
要求精度は ±1μm 以下?
├── YES → サーボモータ
└── NO
├── 高速移動(>500mm/s)が必要?
│ ├── YES → サーボモータ
│ └── NO
│ ├── 負荷変動がある?
│ │ ├── YES → サーボモータ
│ │ └── NO
│ │ ├── コスト優先?
│ │ │ ├── YES → ステッピングモータ
│ │ │ └── NO → サーボモータ(将来性も考慮)
まとめ
| ステッピングモータ | サーボモータ | |
|---|---|---|
| 一言で言うと | 「指示通りに動く職人」 | 「状況を見て調整するプロ」 |
| 制御方式 | オープンループ | クローズドループ |
| 強み | シンプル・低コスト・保持力 | 高精度・高速・高応答 |
| 弱み | 脱調リスク・高速域でトルク低下 | 高コスト・調整が必要 |
| 台形駆動 | 必須(脱調防止のため) | 推奨(機械への衝撃低減) |
両モータはどちらが優れているという関係ではなく、用途と要求仕様に応じて使い分けることが重要です。マシンビジョンのステージ制御においては、要求精度・速度・コストのバランスを考慮して最適なモータを選定しましょう。