XGBoostでMulti-target Time Series Data処理 備忘録

概要

下表に示す時系列問題についてXGBoost適応方法を調べた。

No.	Problem	Note
1	Univariate Uni-target	1種類のXに1つのy
2	Univariate Multi-target	1種類のXに複数のy
3	Multivariate Uni-target	複数種類のXに1つのy
4	Multivariate Multi-target	複数種類のXに複数のy

LSTMではInput Layerや出口のDense LayerのNode数をいじって自在に変更できたが、XGBoostでは初めてだったので手法の調査と前回のToy dataを使った例を備忘録として残す。

尚、XGBoostと相性の良さそうなdataset作成関数series_to_supervised()はJason先生の下記を参照させて頂いた。

• 実施期間: 2022年4月
• 環境：Colab
• パケージ：XGBoost

0. 準備

はじめにColabのXGBoostが0.90とやや古いので入れ直した。

!pip3 install xgboost==1.5.1

今回も下記をImportする。全部使うとは限らない。

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import xgboost as xgb
from xgboost import plot_importance, plot_tree
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split
from sklearn.multioutput import MultiOutputRegressor
print(xgb.__version__)

Jason先生のコードは下記のとおりで、やっていることは元のTime series dataが入っている列(Univariateなら1列、Multivariateなら複数列)のコピーを行方向に1 time stepスライドして追加するというもの。何回追加するかn_inで指定する。Pandas DataFrameならではのアイデア。

def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
    """
    Frame a time series as a supervised learning dataset.
    Arguments:
        data: Sequence of observations as a list or NumPy array.
        n_in: Number of lag observations as input (X).
        n_out: Number of observations as output (y).
        dropnan: Boolean whether or not to drop rows with NaN values.
    Returns:
    Pandas DataFrame of series framed for supervised learning.
    """
    n_vars = 1 if type(data) is list else data.shape[1]
    df = pd.DataFrame(data)
    cols, names = list(), list()
    # input sequence (t-n, ... t-1)
    for i in range(n_in, 0, -1):
        cols.append(df.shift(i))
        names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
    # forecast sequence (t, t+1, ... t+n)
    for i in range(0, n_out):
        cols.append(df.shift(-i))
        if i == 0:
            names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
        else:
            names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
    # put it all together
    agg = pd.concat(cols, axis=1)
    agg.columns = names
    # drop rows with NaN values
    if dropnan:
        agg.dropna(inplace=True)
    return agg

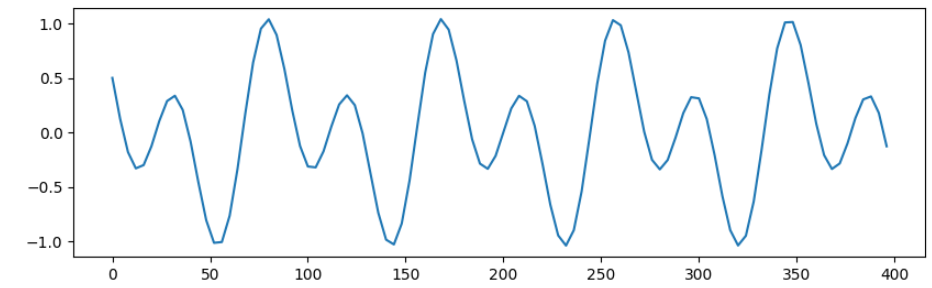
元となるtoy datasetは引き続き下記とし、この波形を予測する。

data_num = 15000
x = np.linspace(0, data_num * 4, data_num)
sin_arr1 = cos_arr1 = 0
sin_arr1 = np.sin(3 * x) /1.5
cos_arr1 = np.cos(1.5 * x) /2
sincos_arr = sin_arr1 + cos_arr1
sincos_lst = list(sincos_arr)

plt.figure(figsize=(10,3), dpi=100)
plt.plot(x[:100], sincos_arr[:100])
plt.show()

1. Univariate Uni-target

Xはtime windowを4としたsincos_lst(=sin+cos)だけ、yも次の1 time stepのsincos_lstだけのケース。

df = series_to_supervised(sincos_lst, n_in=4, n_out=1)
print(df)

つまり、var1(t-4)~var1(t-1)のUnivariateから、var1(t)のUni-targetを予測することになる。
なお追加した各列は行方向に1 time stepスライドし、スライドで発生したNaNを含むsampleをdropしている。従い15000個あったsampleは14996個に減っている。

X = df.iloc[:,0:4]    # var1(t-4)~var1(t-1)
Y = df.iloc[:,4]      # var1(t)

test_size = 0.1
X_train, X_test, y_train, y_test = train_test_split(
        X, Y, test_size=test_size, shuffle = False, stratify = None)

reg = xgb.XGBRegressor(
        n_estimators=10000, random_state=0,
        tree_method='gpu_hist', objective='reg:squarederror')

reg.fit(X_train, y_train,
        eval_set=[(X_train, y_train), (X_test, y_test)],
        early_stopping_rounds=50,
        verbose=False)

# _, ax = plt.subplots(figsize=(5, 6))
# _ = plot_importance(reg, ax=ax, height=0.6)    # 確認したければコメントアウトする

XGBoostのwarningがうるさいので、objective='reg:squarederror'を明示する。またGPUがなければ引数のtree_method='gpu_hist'を削除する。

精度をざっくり確認する。ただし、train_test_split()においてtrain用とtest用のdatasetが切り替わる部分はdataのleakageがtime window分発生すると考えられ、本来test datasetからそのsample（本例では４つ）は除外すべきだろう。

y_pred = reg.predict(X_test)
y_test = np.array(y_test)    # reg.predict()の戻りがnp.array型なので引き算用に同型でcast
print(sum(y_test - y_pred))

-0.0016693047694810118

y_testとy_predの誤差がほとんど無いが、一応描画してみる。

plt.figure(figsize=(20,3), dpi=100)

plt.plot(x[-y_test.shape[0]:], y_test)
plt.plot(x[-y_pred.shape[0]:], y_pred)
plt.show()

2. Univariate Multi-target

Xは同じくsincos_lstだけ、yは連続する2 time stepのdfのケース。

df = series_to_supervised(sincos_lst, n_in=4, n_out=2)
print(df)

つまりvar1(t-4)~var1(t-1)のUnivariateから、var1(t)とvar1(t+1)のMuti-targetを予測することになる。
本投稿の主目的がここである。yに複数の変数があるとき、そのままXGBoostでfit()させようとすると1変数にしか対応していないのかエラーとなる。
そこでRegresserをscikit learnのMultiOutputRegressor()でラップしてあげると、このインスタンスをfitすることで複数のyのfitをいっぺんに行ってくれる。内部では各yに対して個別にfitしているだけだと思うがコードにすると煩雑になるのでありがたい。

下記が参考になった。Classification問題の場合はMultiOutputRegressor()をMultiOutputClassifier()に変えるだけ。

X = df.iloc[:,0:4]    # var1(t-4)~var1(t-1)
Y = df.iloc[:,4:6]    # var1(t),var1(t+1)

test_size = 0.1
X_train, X_test, y_train, y_test = train_test_split(
        X, Y, test_size=test_size, shuffle = False, stratify = None)

xgb_estimator = xgb.XGBRegressor(
        n_estimators=10000, random_state=0, 
        tree_method='gpu_hist', objective='reg:squarederror')

# create MultiOutputClassifier instance with XGBoost model inside
multilabel_model = MultiOutputRegressor(xgb_estimator, n_jobs=2)

multilabel_model.fit(X_train, y_train)

精度をざっくり確認

y_pred = multilabel_model.predict(X_test)
y_test_arr = np.array(y_test)
print(sum(y_test_arr - y_pred))

[-0.00976352 -0.11554188]

var1(t+1)の方がX直後のvar1(t)より精度が悪くなっている。この程度ならほぼ重なってしまうが一応悪い方のvar1(t+1)を描画してみる。

plt.figure(figsize=(20,3), dpi=100)

plt.plot(x[-y_test.shape[0]:], y_test_arr[:,1])
plt.plot(x[-y_test.shape[0]:], y_pred[:,1])
plt.show()

3. Multivariate Uni-target

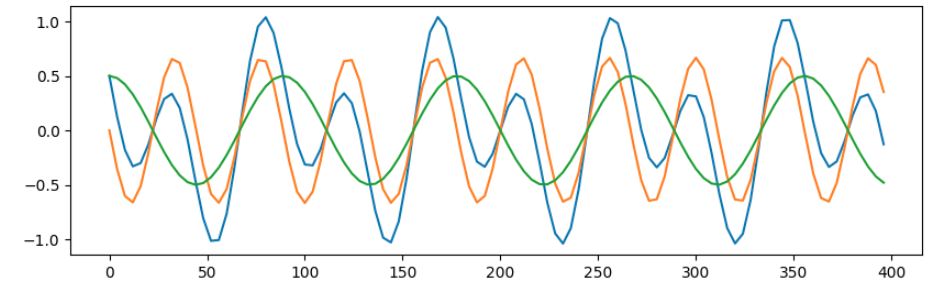
これまでのXは(sin + cos)のUnivariateだったが、MultivariateではXをsinとcosの２種類に分け、yには従前の(sin + cos)とする。

data_num = 15000
x = np.linspace(0, data_num * 4, data_num)
sin_arr1 = cos_arr1 = 0
sin_arr1 = np.sin(3 * x) /1.5
cos_arr1 = np.cos(1.5 * x) /2
sincos_arr = sin_arr1 + cos_arr1
sincos_lst = list(sincos_arr)
sin_lst = list(sin_arr1)
cos_lst = list(cos_arr1)

plt.figure(figsize=(10,3), dpi=100)
plt.plot(x[:100], sincos_arr[:100])
plt.plot(x[:100], sin_arr1[:100])
plt.plot(x[:100], cos_arr1[:100])
plt.show()

Xにはsinの値とcosの値を別々に定義する。その他同じ。

df_raw = pd.DataFrame()
df_raw['sin'] = sin_lst    # Xに追加したい説明変数があればここで追加する
df_raw['cos'] = cos_lst
values_arr = df_raw.values
df = series_to_supervised(values_arr, n_in=4, n_out=1)
print(df)

var1がsinに、var2がcosに対応しているが、y用の最終列もvar1, var2に別れてしまっている。このままではMulti-targetになってしまうので２つを足し合わせたものをvar1+2(t)として列の入れ替えを行う。

df['var1+2(t)'] = df['var1(t)'] + df['var2(t)']
df = df.drop(['var1(t)','var2(t)'], axis=1)
print(df)

つまり、var1(t-4)~var1(t-1)とvar2(t-4)~var2(t-1)のMultivariateから、var1+2(t)のUni-targetを予測することになる。

X = df.iloc[:,0:8]    # var1(t-4)~var2(t-1)
Y = df.iloc[:,8]      # var1+2(t)

test_size = 0.1
X_train, X_test, y_train, y_test = train_test_split(
        X, Y, test_size=test_size, shuffle = False, stratify = None)

reg = xgb.XGBRegressor(
        n_estimators=10000, random_state=0, 
        tree_method='gpu_hist', objective='reg:squarederror')
reg.fit(X_train, y_train,
        eval_set=[(X_train, y_train), (X_test, y_test)],
        early_stopping_rounds=50,
        verbose=False)

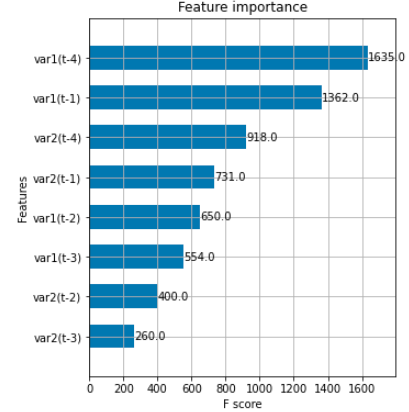
_, ax = plt.subplots(figsize=(5, 6))    #, dpi=100
_ = plot_importance(reg, ax=ax, height=0.6)

精度を確認する。

y_pred = reg.predict(X_test)
y_test = np.array(y_test)
print(sum(y_test - y_pred))

0.09259252133383933

簡単な周期関数で、かつ十分なデータ量があるのに、Xが(sin+cos)のときの精度（誤差の和）が-0.00167だったのに対し、Xをsinとcosに分けると約55倍も悪くなっている。この精度差はXGBoost特有のものか？
本来、説明変数はFeature engineering時に減らすので、普通はsinとcosを分けるようなことはしない。またXGBoostのようなGBDTは和算・減算で与えられた説明変数の特徴を見つけやすいモデルでもある。本来今回のようなdatasetはありえず、深く考える必要はないだろう。

4. Multivariate Multi-target

Xをsinとcosの２種類に分け、yは連続する2 time stepのケース。

df_raw = pd.DataFrame()
df_raw['sin'] = sin_lst
df_raw['cos'] = cos_lst
values_arr = df_raw.values
df = series_to_supervised(values_arr, n_in=4, n_out=2)
print(df)

前出のUni-variate Multi-targetのときと同じ処理を行う。

df['var1+2(t)'] = df['var1(t)'] + df['var2(t)']
df['var1+2(t+1)'] = df['var1(t+1)'] + df['var2(t+1)']
df = df.drop(['var1(t)','var2(t)', 'var1(t+1)','var2(t+1)'], axis=1)
print(df)

つまり、var1(t-4)~var1(t-1)とvar2(t-4)~var2(t-1)Multivariateから、var1+2(t)とvar1+2(t+1)のMuti-targetを予測することになる。

X = df.iloc[:,0:8]    # var1(t-4)~var2(t-1)
Y = df.iloc[:,8:10]   # var1+2(t), var1+2(t+1)

test_size = 0.1
X_train, X_test, y_train, y_test = train_test_split(
        X, Y, test_size=test_size, shuffle = False, stratify = None)

xgb_estimator = xgb.XGBRegressor(
        n_estimators=10000, random_state=0, 
        tree_method='gpu_hist', objective='reg:squarederror')

# create MultiOutputClassifier instance with XGBoost model inside
multilabel_model = MultiOutputRegressor(xgb_estimator, n_jobs=2)

multilabel_model.fit(X_train, y_train)

精度を確認する。

y_pred = multilabel_model.predict(X_test)
y_test_arr = np.array(y_test)
print(sum(y_test_arr - y_pred))

[ 0.07832569 -0.01344732]

今度はt+1の方がやや良くなったが、いずれにせよどちらも良い。

5. まとめ

Multi-targetの方法を知ることが目的だった。
精度は実際の問題時に与えられる説明変数によるので、今回は参考、というかデバッグ程度に留める。
前回発見したFFTっぽい説明変数など実際には組み合わせて、精度がどのように変化するか実務で確認する。

以上