XGBoostでTime Series Data処理 備忘録

概要

仕事でtime series datasetをまた扱うことになった。LSTMに入れる前にXGBoostで味見してみようと手弁当で下調べ中、下記サイトを見つけた。
日付の処理の仕方が興味深く、だったらdatetimeデータがなくてもい行けるんじゃね？とただの数字の羅列を説明変数に入れてみた備忘録。

• 実施期間: 2022年3月
• 環境：Colab
• パケージ：XGBoost

Time series dataset (Seasonal)

はじめにColabのXGBoostが0.90とやや古いので入れ直した。

!pip3 install xgboost==1.1.1

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import xgboost as xgb
from xgboost import plot_importance, plot_tree
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split
print(xgb.__version__)

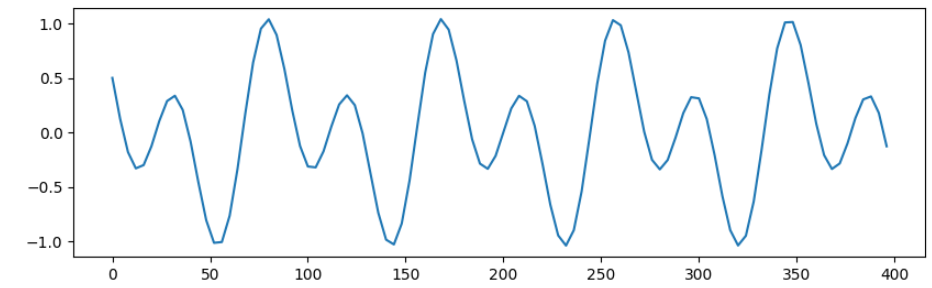
prediction対象は、完全syntheticでseasonalな三角関数とする。そのままでは面白くないのでsin + cosとした。

data_num = 15000
x = np.linspace(0, data_num * 4, data_num)
sin_arr1 = sin_arr2 = sin_arr3 = 0
sin_arr1 = np.sin(3 * x) /1.5
sin_arr2 = np.cos(1.5 * x) /2
# sin_arr3 = np.cos(8 * x + 1) /2    # 時間かかるので使わん
sin_arr = sin_arr1 + sin_arr2 + sin_arr3

plt.figure(figsize=(10,3), dpi=100)
plt.plot(x[:100], sin_arr[:100])
plt.show()

このsin_arrを予測する。

前述のKaggleの例では日付や月やwork weekなどを数値化してそれぞれをfeatureにされていた。この考え方がOKなら今回のようなdatetimeを持たいないseries dataでも、datetimeに相応するN進数データをfeatureにすればいいんじゃないかと。
ここでは8進数、9進数、...、49進数までをfeatuerとして追加する。三角関数の周期性をこのうちのいくつかが説明してくれるだろうという目論。ちなみに2~7進数はfeature importanceが小さかったので入れない。

df = pd.DataFrame()
for i in range(8, 50, 1):
    x2_ = list(np.arange(0,i))
    x2_ = np.array(x2_*10000)   # 10000：スライスしてトリムするから十分大きなどうでも良い値
    x2_ = x2_[0:data_num]
    df[i] = x2_

df['val'] = sin_arr

print(df)

TrainingとFeature Importance

特に説明はない。

X = np.array(df.iloc[:,0:42])
Y = np.array(df.iloc[:,42])

test_size = 0.1
X_train, X_test, y_train, y_test = train_test_split(
        X, Y, 
        test_size=test_size, 
        shuffle = False, stratify = None)

reg = xgb.XGBRegressor(n_estimators=10000, 
        tree_method='gpu_hist', random_state=0, 
        objective='reg:squarederror')

reg.fit(X_train, y_train,
        eval_set=[(X_train, y_train), (X_test, y_test)],
        early_stopping_rounds = 100,
        verbose = True)

feature importanceを確認する。

_, ax = plt.subplots(figsize=(10, 8), dpi=100)
_ = plot_importance(reg1, ax=ax, height=0.6)

上位から順にf35は44進数、次のf38は46進数、f15は23進数を示す。
おそらくf35,38は波高値大きなsin関数を説明し、f15は周期を倍にしたcos関数を説明しているような気がする。さながらXGBoostを使ったFFTのような感じ。

Predictionと精度確認

Prediction結果を描画する。

y_pred = reg1.predict(X_test)

plt.figure(figsize=(20,3), dpi=100)

plt.plot(x[-y_test.shape[0]:], y_test)
plt.plot(x[-y_pred.shape[0]:], y_pred)
plt.show()

いい感じに見える。簡単にy_testとy_predの差も確認する。

print(sum(y_test - y_pred))

-7.227987089052772

Time series dataset (Seasonal + Trend)

前述のsin_arrに0.5/15000の勾配でtrend成分を加えてみる。
N進数はうまくsin+cosのseasonality(周期性)を説明したがこの一定の勾配を説明するfeatureがないので精度が悪くなることを期待して確認する。

data_num = 15000
y_trend = np.linspace(0, 0.5, data_num)
print(y_trend)
sin_arr = sin_arr + y_trend

途中割愛し、feature importanceを見てみる。

どのfeatureを見てよいのか迷っているみたい。
予測結果は下図のように周期はあっているが波高値は先に進むに連れ悪化している。思惑通り一定勾配を説明するfeatureがないからだろう。

print(sum(y_test - y_pred))

324.42460065419976

以上