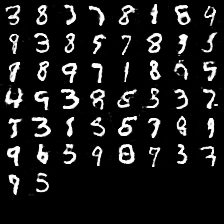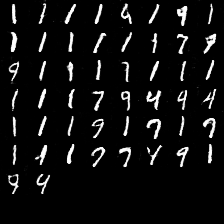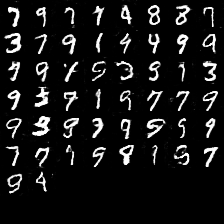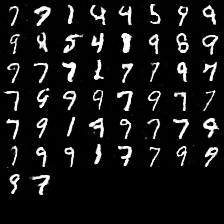0. この記事の嬉しいところ
- ディープラーニングで生成したデータを 3Dプリンタ で印刷する流れがわかる (10. 実験用コードにおいて、全コード GitHub に上げてます。
git cloneして環境さえ作れば、同じことが簡単にできるはずです。環境の作り方はこちらに書いています。) - 材料力学の勉強になる (僕も勉強しながら書いてますが…)
- TensorFlow 2.0 のテンソル操作を材料力学に応用する仕組みが分かります
※ スマホで見ると結構崩れるようなので、PC推奨記事です。
1. 概要
- DCGAN (Radford et al., 2016)1 を利用し、そのロス関数に強度情報を加えることで、強度の高い数字を生成できるようにした
- データのコンセプトを維持したまま強度を操作できる
- ロスの設計やパラメータ変更により、強度を増減させられる
- 生成画像の FID (Heusel et al.,2017)2 (どのくらい元のデータの多様性や形状を維持しているか) と強度のトレードオフを発見した
- 医療画像などへの応用の可能性、GAN そのものの改善への可能性を見つけた
- 生成した断面を 3Dプリンタ で印刷した
- Danmen-GAN と名付けておく(名前が無いと呼びにくいので)
(記事が長いですが、3/4くらい画像かオマケなのですぐに読めると思います。)
2. 背景
最近、3Dプリンタを入手したので、3Dプリンタ x ディープラーニング の組み合わせで何かできないか考えていたら思いついたので、やってみることにしました。
材料力学の基礎理論はここ百年ほど変化していないらしいので、自由度の高いディープラーニング側から歩み寄っていきたかったです。
0-9 のどの数字が頑丈が予想しながら読むと楽しめるかもしれません。一種類頭飛び抜けて頑丈な数字があります。
(※ 材料力学の本 (日本機械学会, 2007)3 を読みながらやっているので適当なこと言ってるかもしれないです。間違いがあったら修正します。一応ざっと GAN 側の研究を探した範囲では似たような研究が見つからなかったのですが、あったら教えて下さい。)
3. 理論
興味がない人は、読み飛ばしても全然問題ないと思います。
3.1 断面二次モーメント
そもそも、強度というざっくりした言葉には複数の指標があります。
材料屋さんがどう言う風に強度という言葉を使っているのか知りませんが、我々一般人は色々な意味で強度という言葉を使います。
モース硬度、ビッカース硬度、降伏応力(引張強さ)、などなど…
その中でも特に支配力が強く、素材に依存せず断面の形状のみによって決定する強度が、断面二次モーメント です。これは、どのくらいその部材が曲がりにくいか、という係数になります。
力を加えると、大抵のものはその力に比例して目には見えないレベルで微妙に曲がります。
そして、曲がりすぎると大抵のものは、へし折れて戻らなくなったりします。
逆に言うと、強力な断面をもつ部材ほど壊れにくいということになります。
例えば、新聞紙はペラペラのままだと何も支えられませんが、丸めるだけでそこそこ堅くなります。
(紙の厚みが増す要因もありますが)
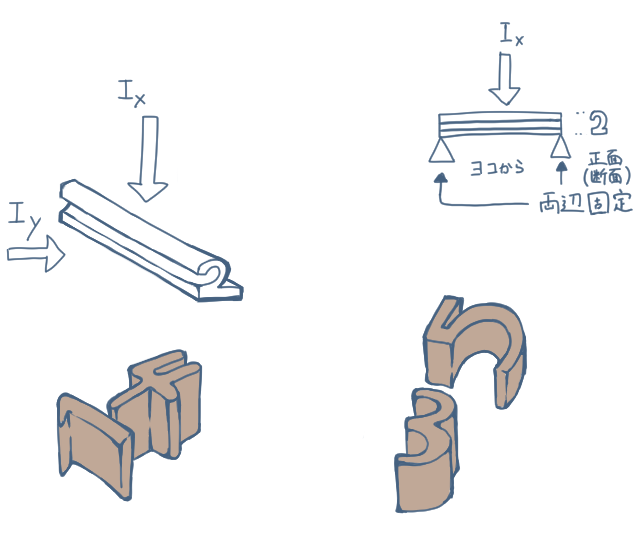
日本機械学会は 3 5章 p63 において、「細長い棒に横方向から棒の軸を含む平面内の曲げを引き起こすような横荷重を受けるとき、このような棒をはり(beam)と呼ぶ。」 と定義しています。
この画像における、「2」の形状をした細長い棒の両側を固定すると「はり」になります。
このとき矢印の向きに対する、縦からの力に対する断面二次モーメントが $I_x$、また、横からの力に対する断面二次モーメントが $I_y$ になります。
$x$ と $y$ の向きが画像処理の軸と転置しているのでちょっとややこしいです。
ウィキペディア先輩5 もそう言ってるし、たぶんこれがスタンダードなんでしょう。
次に、断面二次モーメントの計算方法を説明します。
縦軸からの力に対する断面二次モーメント $I_x$ は、
$$
I_x = \int_A y^2 dA \tag{1}
$$
で計算できます。
ここで、$A$ は断面積、$y$ は中立軸 (断面の重心) からの上下方向の距離を表します。
同様に、横軸からの力に対する断面二次モーメント $I_y$ は、
$$
I_y = \int_A x^2 dA \tag{2}
$$
で計算できます。ここで、$x$ は中立軸からの左右方向の距離を表します。
また、断面二次極モーメントという、「ねじり」に対する断面の強さを表す指標もあり、
$$
I_r = I_x + I_y \tag{3}
$$
と計算できます。せっかくなのでこの強度も実験に導入します。
「ねじり」というのは雑巾を絞るときにかかる回転の力、をイメージすると分かりやすいです。
これら三指標は全て単位が、m^4 になります。
距離の差の二乗[m^2]を面積で積分[m^2]しているのでこうなります。
具体的には、単純な長方形断面の場合の断面二次モーメントは、
- $I_x$ は、(厚みの三乗)$\times$(幅の一乗)
- $I_y$ は、(厚みの一乗)$\times$(幅の三乗)
に比例するのが直感的に分かると思います。
では、今回の場合どうなるのでしょうか?
まず、理解しやすくするため、全ピクセル値=1.0(最大値) の画像の断面二次モーメントを可視化します。
| 画像 | $\Delta I_x$ | $\Delta I_y$ |
|---|---|---|
 |
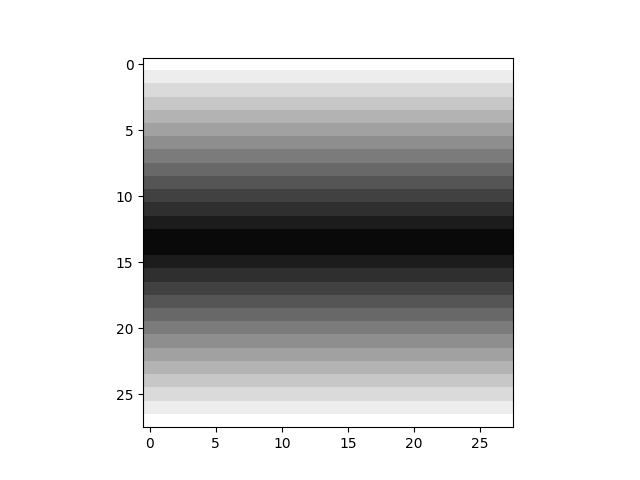 $I_x=1.000$ (MAX) $I_x=1.000$ (MAX) |
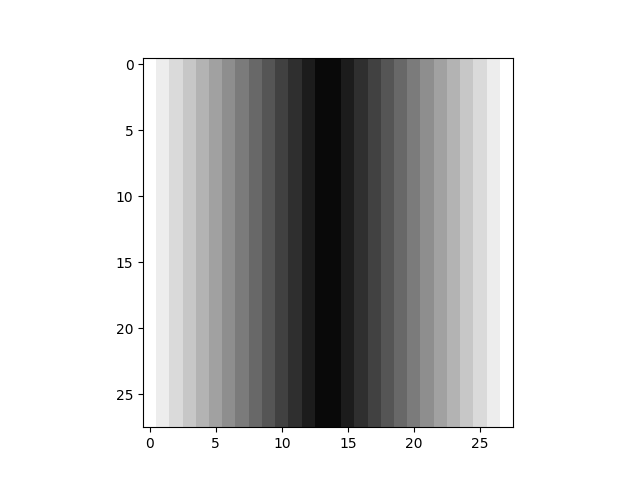 $I_y=1.000$ (MAX) $I_y=1.000$ (MAX) |
ここで、$\Delta I_x$ は、単位ピクセルごとの断面二次モーメント $I_x$ への影響、$\Delta I_y$ は、ピクセルごとの断面二次モーメント $I_y$ への影響です。これらを合計することで、$I_x$ と $I_y$ が求まります。
また今回は、メートル単位とは切り離し、この正方形を最大の断面二次モーメント $1.0$ としておきます。
同様の図を、MNIST の一部のデータで表示してみましょう。
(0.0 < 画素値 < 1.0 の値に関しては、画素値と面積が比例しているという近似をしています。
つまり、画素値が0.5だとピクセルの半分に断面が存在しない、0.1だと九割欠損という仮定です。※これは最終的な印刷時にはどうしても別の近似になってしまいます。)
| 画像 | $\Delta I_x$ | $\Delta I_y$ |
|---|---|---|
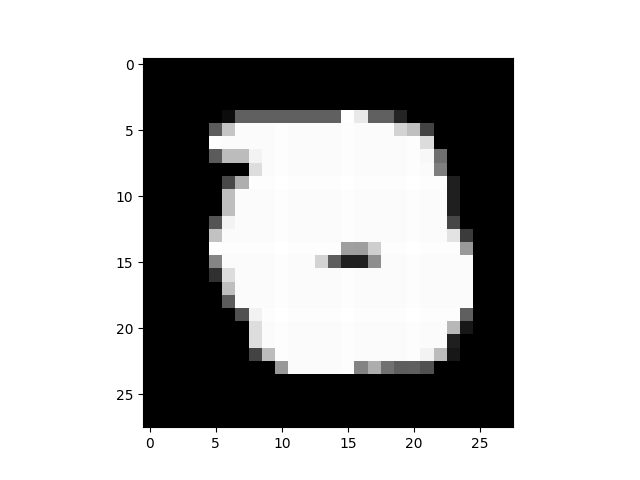
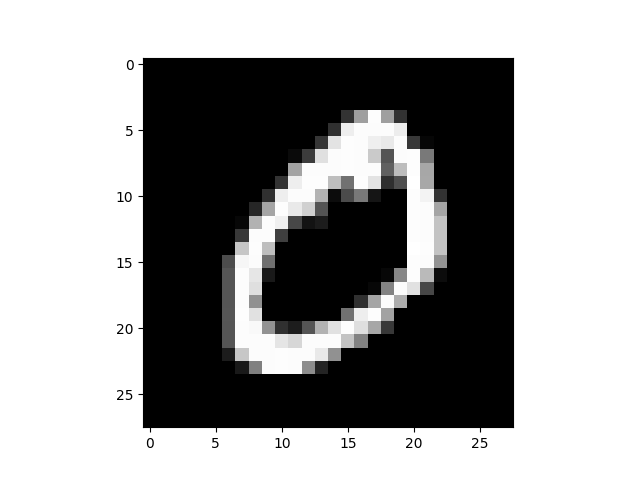 |
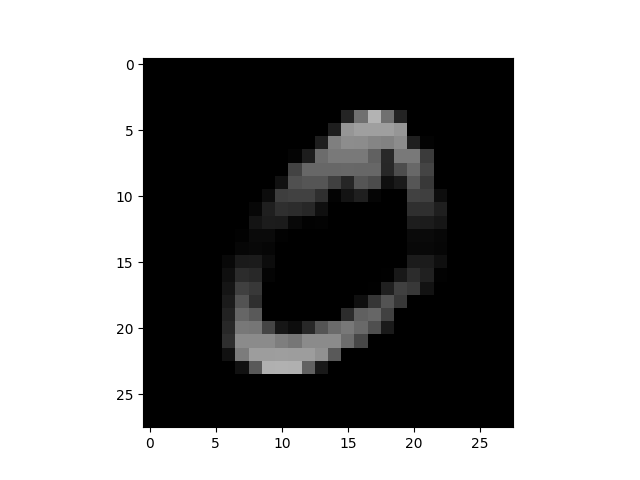 $I_x=0.112$ |
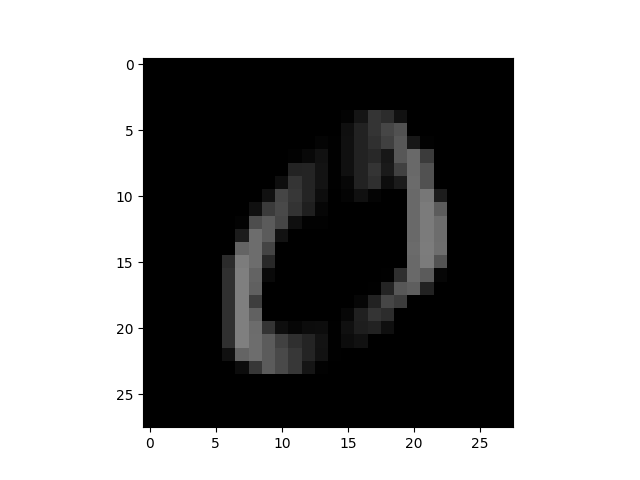 $I_y=0.093$ $I_y=0.093$ |
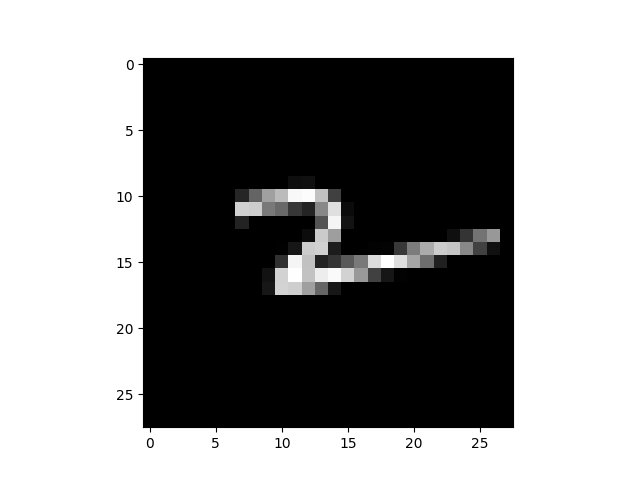
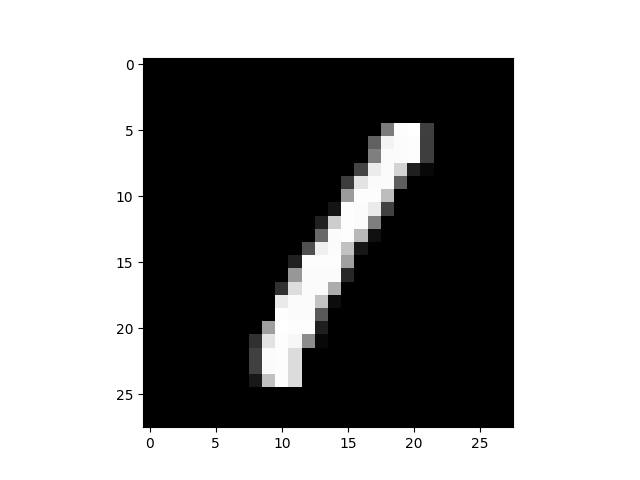 |
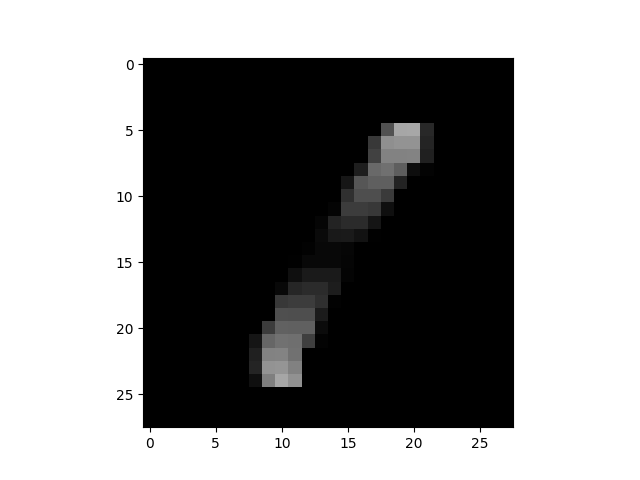 $I_x=0.060$ $I_x=0.060$ |
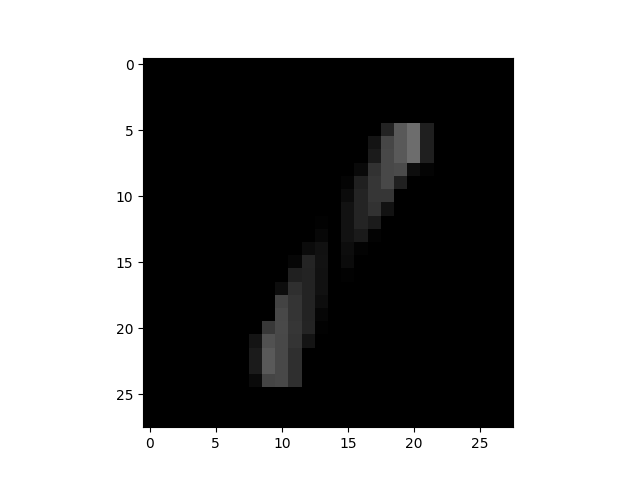 $I_y=0.036$ $I_y=0.036$ |
「0」は $I_x$, $I_y$ の両方とも高いですが、特に縦方向の強度が強いのがわかります。
逆に、「1」は $I_x$, $I_y$ の両方とも低く、特に横方向の強度がほぼ無いです。
断面二次モーメントの計算をすると、強度は中立軸から距離があるほど影響力が強く、中立軸に近いほど影響力が低いです。これらを考えると、世の中の大抵の構造物が中空 (中身がスカスカ) なのは、断面二次モーメントによる影響がそこそこ大きいです。
以上より、素材と重量を抑えつつ、強度が高い代表的な断面は、中空の円形・四角形や、H型/I型(片軸の強度のみ強い) などが該当します。今回は、特に素材の重量などの制約は存在しないので、最も頑丈な形状は画像の画素値が埋まっている "正方形" になります。
では、強度を維持したまま数字の形状を保つにはどうしたらいいのでしょうか?
3.2 Generative Adversarial Nets (Goodfellow et al., 2014)6
基本的な Generative Adversarial Nets (=GAN) はニューラルネットワークのモデルを二つ使用し、片方がデータに近い分布を出力する Generator、もう片方が Generator、もしくは、データの入力に対し、それが生成されたものか否かを判断する Discriminator から成ります。
Discriminator の判断が正確であるほど、誤差逆伝播法により、Generator のパラメータに修正が入り、Generator はよりデータらしい分布を生成するようになります。
一方、Discriminator の判断の正確性の低さは、Discriminator 自身のペナルティとして、判断の精度を上げられるようパラメータに修正が入ります。
これらは、Goodfellow らの式(4)の定式化 6 から来ています。
\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))] \tag{4}
噛み砕いて説明すると、数字の画像データにこれを当てはめると、Generator 側は数字っぽい画像を生成するよう学習が進み、学習が成功するとデータセットに存在しない数字さえ生成してくれるようになるということです。
また、GAN の理論や学習法に関しては様々な手法が考案されていますが、今回は古典的な DCGAN 1 がベースになっています。DCGAN とは、一言で言ってしまうと、GAN の基本的な手法を畳み込みニューラルネットワークに応用した論文です。
3.3 Danmen-GAN
基礎技術の説明が終わったので、今回頑丈な数字を作成するためのロジックを書きます。
通常の GAN の学習で、Generator にかかるロスは、式(5)になります。
これは、ノイズを入力としたときの Generator の生成結果を Discriminator が受け取り、Discriminator が正解してしまった割合でロスが強くなるものです。
\mathcal{L}_{G} = \mathbb{E} [\log (1 - D(G(z))] \tag{5}
ただ、これだけだとランダムに数字が生成されるように学習が進むだけなので、入力画像の断面形状から断面二次モーメントを計算する関数 $S(\cdot)$ を組み込み、生成された断面画像の断面二次モーメントが低いほど Generator にペナルティがかかるような、新たなロス $\mathcal{L}_{S}$ を作成します。
\mathcal{L}_{S} = \mathbb{E} \left[\|1 - S(G(z))\|_{2}\right] \tag{6}
また、$S(\cdot)$ に、縦方向 x、横方向 y、ねじれ r の軸を導入し、それらをパラメータ α, β, γ で重み付けすると、式(6)は、式(7)になります。
\mathcal{L}_{S} = \alpha \cdot\mathbb{E} \left[|1 - S_x(G(z))|_2\right] + \beta \cdot\mathbb{E} \left[|1 - S_y(G(z))|_2\right] + \gamma \cdot\mathbb{E} \left[|1 - S_r(G(z))|_2\right]
最後に、GAN の Generator 側のロスに、式(7)を加え、式(8)とし、完成です。
\mathcal{L}_{All} = \mathcal{L}_{G} + \mathcal{L}_{S} \tag{8}
式(8) を Generator の目的関数とすることで、断面が数字の形状を維持しつつ、断面二次モーメントを高めることができるというロジックです。
4. データ分析
データセットは MNIST 4 です。
今回は生成データの元さえあればいいので、学習データのみ使用します。
まず、データセット内部の強度がどのくらいあるか把握しておきたいので、計算することにします。
4.1 グローバルな強度
データセット全体の各軸に対する平均断面二次モーメント $\mathbb{E} \left[I_x\right]$, $\mathbb{E} \left[I_y\right]$, $\mathbb{E} \left[I_r\right]$ を求めました。
また、それぞれの統計値について、断面二次モーメントの標準偏差 $\sigma_{Ix}$, $\sigma_{Iy}$, $\sigma_{Ir}$ も計算しました。
| $E[I_x]$ ($\sigma_{Ix}$) | $E[I_y]$ ($\sigma_{Iy}$) | $E[I_r]$ ($\sigma_{Ir}$) |
|---|---|---|
| 0.088(0.032) | 0.063(0.034) | 0.076(0.031) |
この表を見ると、そこそこデータによって断面二次モーメントにバラつきがあるように感じます。
また、全体的に横方向より、縦方向の強度の方が大きいことが分かります。
4.2 数字ごとの強度
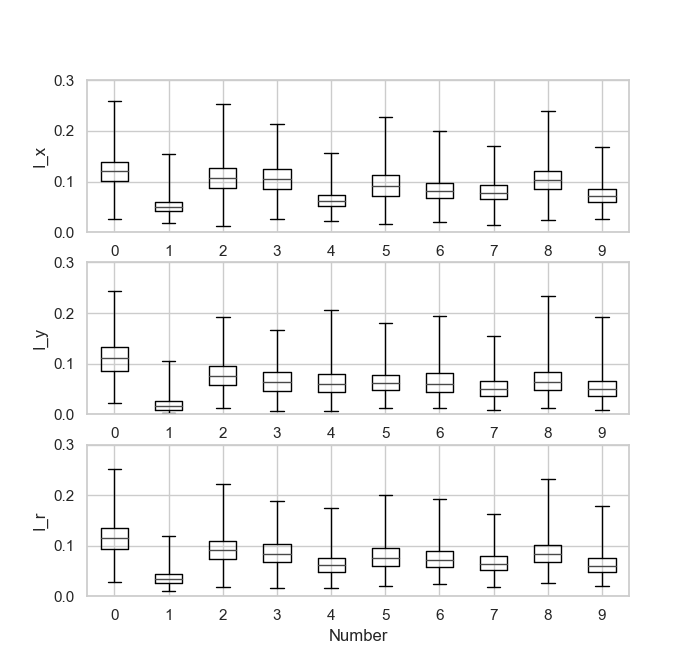
次に、数字ごとに形状に偏りがあると考え、数字ごとの断面二次モーメントの統計値をまとめました。
これを箱ひげ図と表のセットで表します。異常値に対する処理はしていません。
| Number(n) | $E[I_{xn}]$ ($\sigma_{Ixn}$) | $E[I_{yn}]$ ($\sigma_{Iyn}$) | $E[I_{rn}] $ ($\sigma_{Irn}$) |
|---|---|---|---|
| 0 | 0.121(0.029) | 0.110(0.034) | 0.116(0.030) |
| 1 | 0.052(0.015) | 0.020(0.014) | 0.036(0.013) |
| 2 | 0.107(0.031) | 0.078(0.027) | 0.093(0.027) |
| 3 | 0.106(0.028) | 0.066(0.026) | 0.086(0.026) |
| 4 | 0.064(0.018) | 0.063(0.026) | 0.064(0.021) |
| 5 | 0.093(0.031) | 0.065(0.024) | 0.079(0.026) |
| 6 | 0.083(0.022) | 0.065(0.028) | 0.074(0.024) |
| 7 | 0.079(0.021) | 0.053(0.022) | 0.066(0.020) |
| 8 | 0.105(0.027) | 0.067(0.027) | 0.086(0.026) |
| 9 | 0.074(0.019) | 0.054(0.024) | 0.064(0.021) |
これらから、以下のことがわかります。
- $I_x$ も $I_y$ も基本的には「0」が強い
- 「1」の $I_y$ が圧倒的に低い
- 微妙なところだと、「2」「3」「8」がそこそこ強い
- 平均値を見ると数字によって断面二次モーメントにバイアスがあるが、(1以外) 画像によってバラつきが大きいので頑張れば「0」に勝てるかもしれない
4.3 最強と最弱
最強の強度を持つ数字と、最弱の数字を argmax/argmin で調べてみました。
最強は当然「0」なのですが、
ペンの幅太すぎじゃないですかね…
ちなみに、$I_x=0.259$, $I_y=0.244$, $I_r=0.251$ と、全分野でトップです。
これを書いた人は誇っていいです。
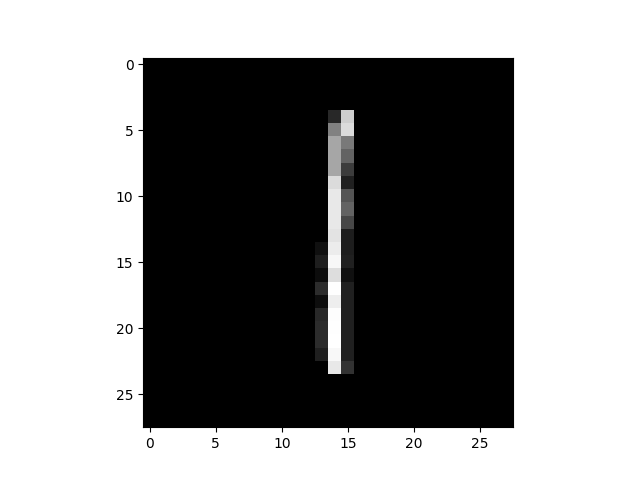
次に、$I_x$ の最弱を紹介します。
「2」なんですが、めちゃくちゃ潰れてますね。
計算的にも、最も潰れてる数字でもあると思います。
弱そう。($I_x=0.013$)
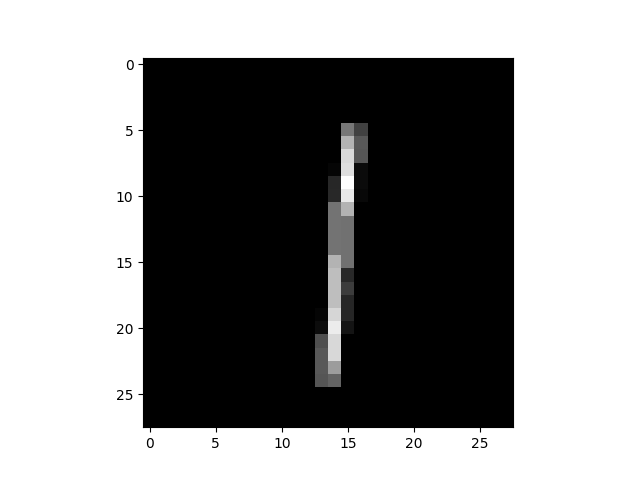
そして、$I_y$ の最弱
細すぎ。横から力かけたら折れそう。($I_y=0.0015$ ← 小さすぎるので桁を下げました)
最後に、$I_r$ の最弱
一見、一個前の「1」と似ていますが、若干傾いています。($I_r=0.010$)
機械学習のデータセットは個性があっていいですね。
5. 実験
それでは実験を行いましょう。
TensorFlow 2.0 で理論通りのモデルを組み、式(8)のロス関数を Generator に適用した GAN を学習しました。
モデルは Appendix にオマケとして付けておきました。
コードは全部 GitHub に上げておきました。
- 全ての実験は、Colaboratory(K80) で実行
- 計算時間は、一つの学習あたり一時間程度 (大部分がFIDの計算時間)
- バッチサイズ:50
- エポック数: 20 (計24,000イテレーション)
- FID は 5,000枚 で比較
- データ拡張なし
バージョンなど
- numpy 1.18.4
- tensorflow 2.2.0
- stealthflow 0.0.13
- その他 matplot, seaborn など(計算に影響がない)
5.1 各種パラメータと生成結果
5.1.1 Danmen-GAN
最小 FID は、その学習中に達した最小のFID値です。(FID は小さいほどよいです。)
また、FID の比較対象は、生成画像と、学習データです。
グラフは、α を変化させたときの、$I_x$ と $FID$、$\frac{I_x}{FID}$ の変化です (β=γ=0)。
このグラフから、断面二次モーメントを得る代わりに、FID を犠牲にしていることが明確になります。
出力画像の変化 (β=γ=0)。
下に行くほど、縦に対する強度が増すようにしています。
やはり「0」が強いですね。データセットのバイアスのせいだと思います。
ロスをかけなくても、平均の $I_x$ よりも二割高い断面二次モーメントを持つ断面が生成されているので、そもそも通常の GAN 自体強度にバイアスがかかっているみたいです。
これはノイズを生みやすい、などの GAN の基本的な挙動に起因しているのかもしれないですね。
$\alpha=50.0$ レベルまで行くと、元データの異常値クラスの強度を平均的に生成できるようなので、数の少ないデータを GAN で生成するデータ拡張に応用できる可能性を感じます 。例えば、医療診断用画像ならば、核磁気共鳴法 T1/T2 強調画像などありますが、T1 のとき腫瘍はやや白く見える 7 らしいので、画像のピクセル値が増えるようなロスをかけることで、極端に大きな腫瘍をもつ生成画像を作れる可能性が考えられます。あとは、脳などは、断面の外側 (外側溝や大脳皮質) や内側 (海馬や脳梁) などで性質が変わるので、おそらく疾患の傾向も変化するはずです。これによって目的の疾患に合わせた GAN のデータ拡張により、疾患に近い形の画像を生成できるかもしれないと考えました。
(医療何も知らないので適当なこと言ってるかもしれません…)
$I_y$, $I_r$ の例
これらも「0」が強いですね。ちゃんと他の数字も出たりしているので、モードコラプスにはなってなさそう。
5.1.2 数字の弱体化
Danmen−GAN の理屈を応用して、目的の断面二次モーメントを0.0にし、強度を減少させることができます。
これは、式(9)で表せます
\mathcal{L}_{S} = \mathbb{E} \left[\| S(G(z))\|_{2}\right] \tag{9}
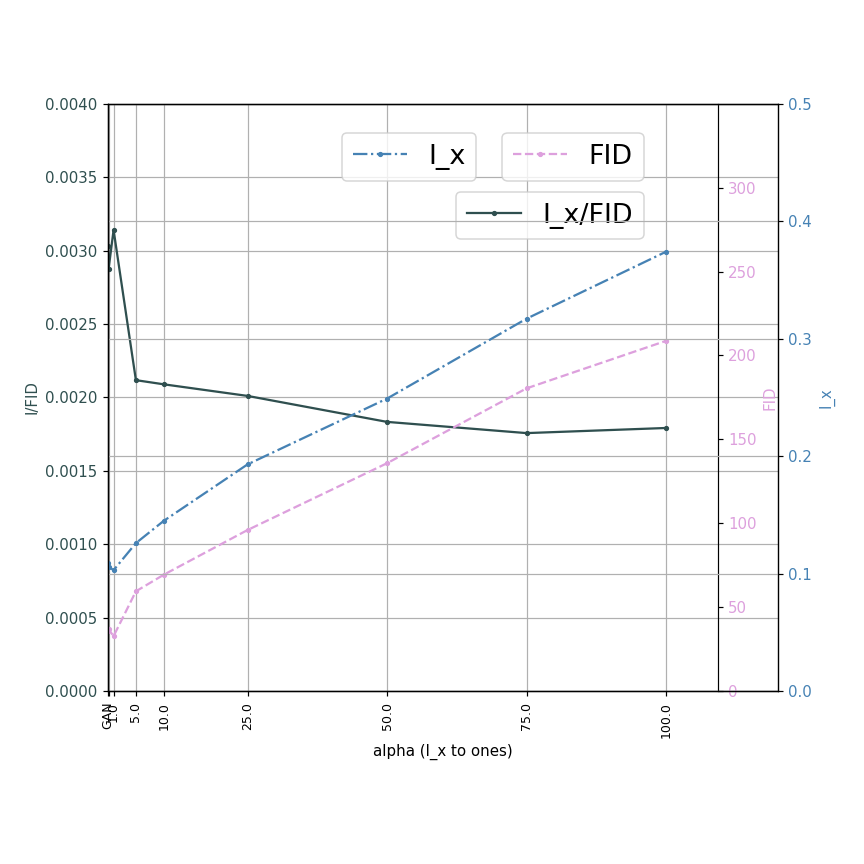
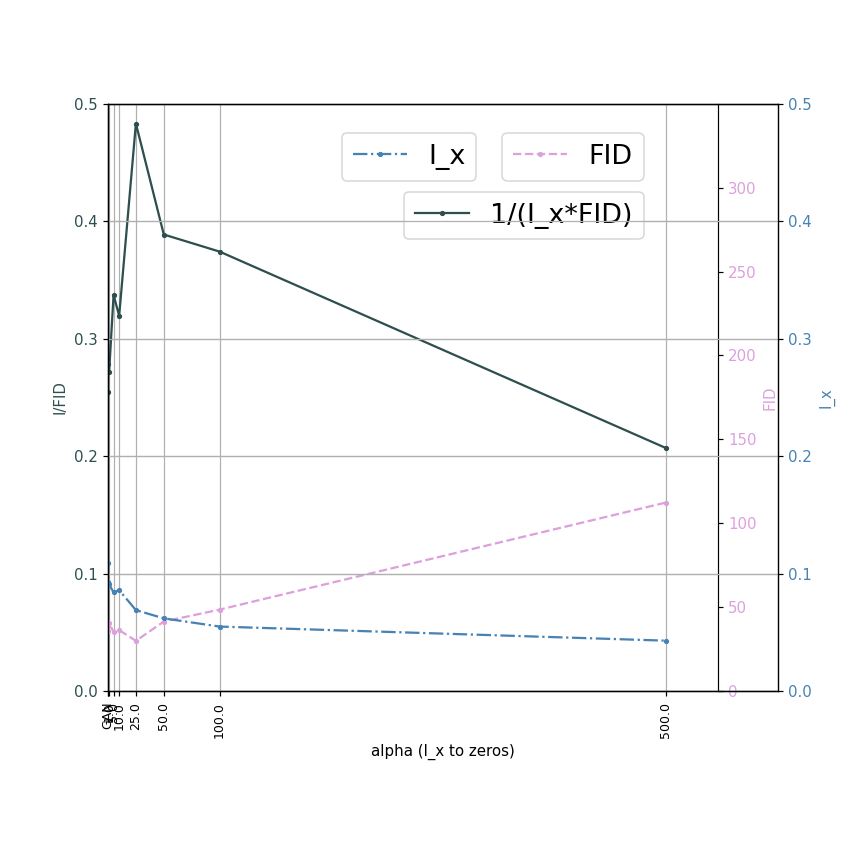
このグラフは、 $\alpha$ を変化させたときの、$I_x$ とFID、$\frac{1}{I_x\times FID}$ の変化です (β=γ=0)。
断面二次モーメントを減らす場合も、やはり FID は犠牲になります。これは元データの分布と離れるということは増やす場合と同じであるからです。
出力画像の変化 ($\beta=\gamma=0$)
やはり、元々強度の低い「1」が多く出る傾向になります。しかもほっそりしてる気がする。
パラメータのスケールが断面二次モーメントを強化するときと変化しており、こちらのほうが強くかけても影響がでにくいようです(おそらくピクセルの比率のせい)。
$I_y$, $I_r$ の例
これは可能性の話ですが、強度を下げる方にロスをかけると、ノイズごと抑制され、FID が改善される可能性 を考えています。特に、断面二次モーメントの計算は画面の端に強いロスをかける性質を持っており、CNN は画面の端の処理で padding などの怪しいことを行っているので、相性が噛み合っている可能性はあります。特に断面二次極モーメント $I_r$ は画面の端全体に影響が及ぶので効果的かもしれません。
これは、ただの偶然の結果かもしれないので、個人的に深堀りしてみようと思います。
5.2 断面二次モーメント vs FID
断面二次モーメントの伸びに対して FID の上昇をどれだけ抑えられているか確かめました。
$\frac{I_x}{FID}$ は学習中で最大のものを取得しています。
断面二次モーメントの微妙な上昇に対し、FID は爆増してしまうので、強度を得る代わりに元データの分布から離れてしまうようです。
| $\alpha$ | $\frac{I_x}{FID}$ |
|---|---|
| $\alpha=0.0$ | 0.00250 |
| $\alpha=0.1$ | 0.00250 |
| $\alpha=1.0$ | 0.00277 |
| $\alpha=5.0$ | 0.00207 |
| $\alpha=10.0$ | 0.00220 |
| $\alpha=25.0$ | 0.00180 |
| $\alpha=50.0$ | 0.00150 |
| $\alpha=75.0$ | 0.00130 |
| $\alpha=100.0$ | 0.00120 |
| ones | 0.00257 |
ones は、全てが 1.0 の場合の断面です。このときの FID は 394.5 でした。
これだと、全て 1.0 の出力か、愚直に数字を出力するほうが $\frac{I_x}{FID}$ のパフォーマンスはいいことになってしまいます。逆に考えると、FID を計算するレイヤーを作り、$\frac{I_x}{FID}$ をロスとして設計したら、また異なる結果が出てきそうで面白そうですね。
(FID のレイヤーは作れましたが8、どうしても行列の平方根を求める部分が計算としてボトルネックになりすぎたので、やめました。原理的には可能という概念。)
最終的に、データセットの最強を超える断面の生成には成功しましたが、最弱より弱い断面の生成はまだ確認できていません (もっと強くロスをかければいけるかもしれませんが)。
6. 3D プリンタによる印刷
せっかくなので、3Dプリンタ で印刷して強度を確認してみましょう。
使用したのは、Ender-3 という機種で通販サイトなどで2-3万する機種です。
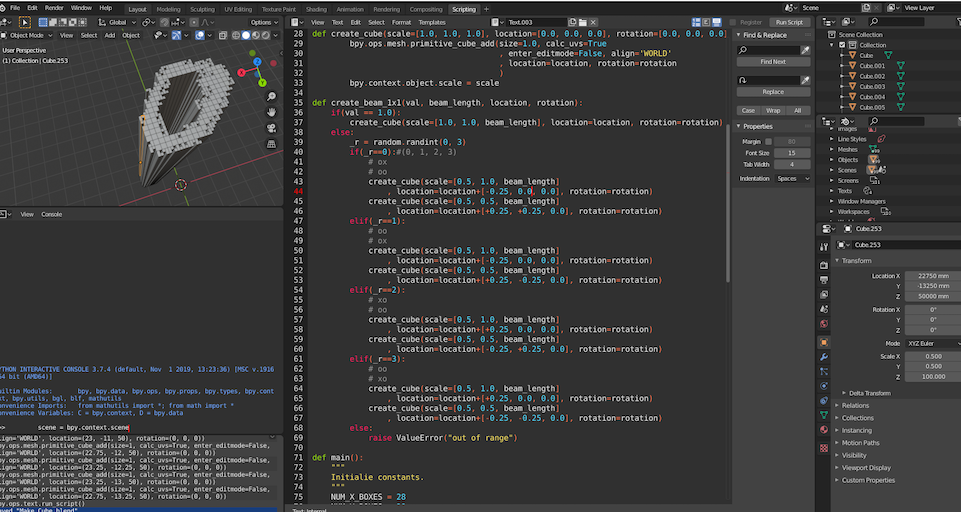
6.1 Blender で TensorFlow 2.0 を動かし、数字ポリゴンの自動生成
Blender 側では、こんな感じで自動生成を行います。
下の画像は MNIST データにある一番目の「0」です。
ピクセルに対応する部分を add_cube で自動生成しています。
(やり方がかなり雑なので3D屋さんに怒られてしまいそう)
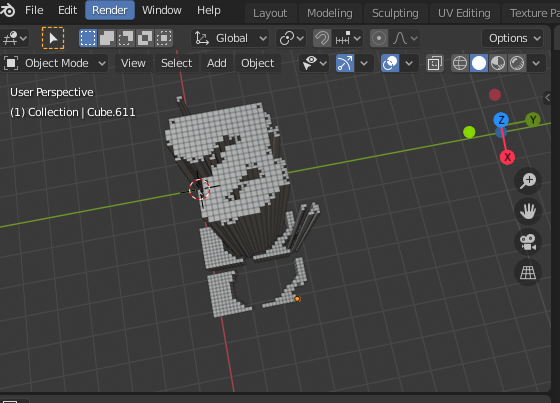
下の画像は、$\alpha=75$ でペナルティをかけた Danmen-GAN で生成した「8」っぽい数字です。
bpy というモジュールで、Blender の API を Python で操作できるので、Blender 上の Python で TensorFlow の学習済みモデルを読み込み、その場で生成を行います。とても便利。
0.25 以下のピクセル値は 0、0.25~0.75 のピクセル値はランダムに穴を開け 3/4 の面積に (少し穴が開いて強度が下がる)、0.75 以上のピクセル値は 1.0 とするヒューリスティックで、とりあえず曖昧なピクセルを処理します。
強度に関係ない部分は、手作業で除去します。
(印刷効率を上げるため)
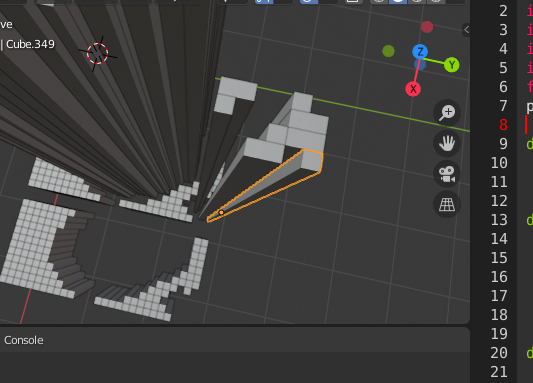
以下が整えた後の断面になります。

数字の下側にある断片みたいなものは、部材を固定するための台座みたいなイメージで作りました。
これは、数字のピクセルを反転 (1.0 - img) したものを np.ceil() で切り上げ、scikit-image の収縮処理 (skimage.morphology.binary_erosion) をかけ、調整し、for文 でセットにしたものです。
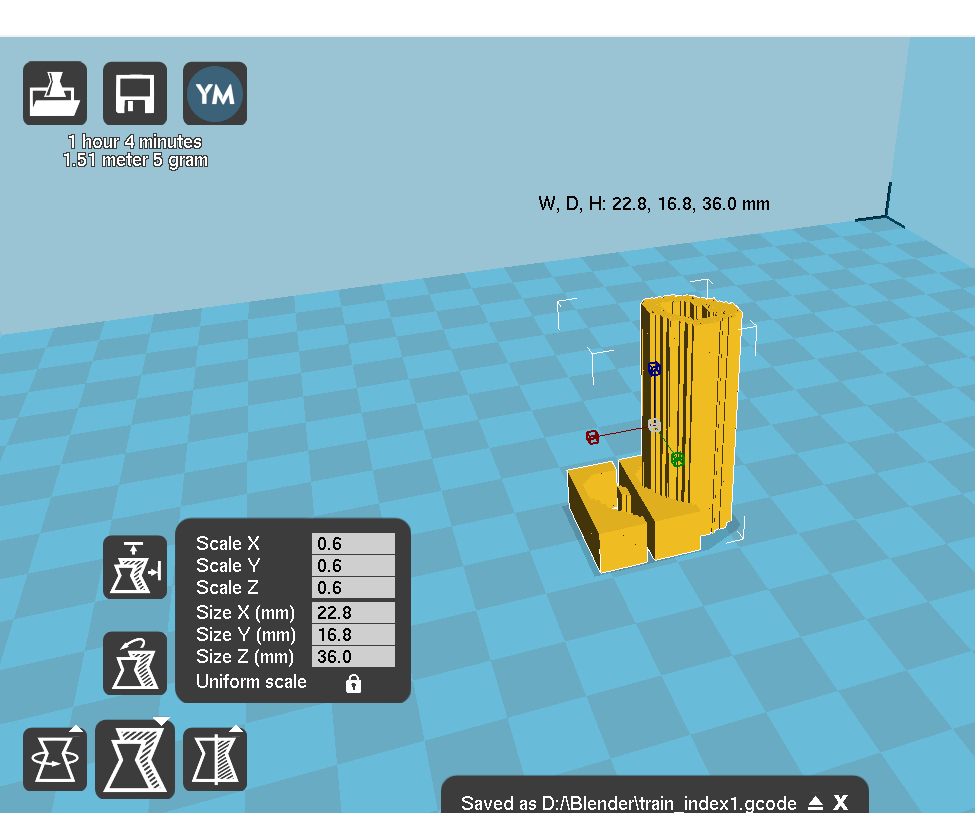
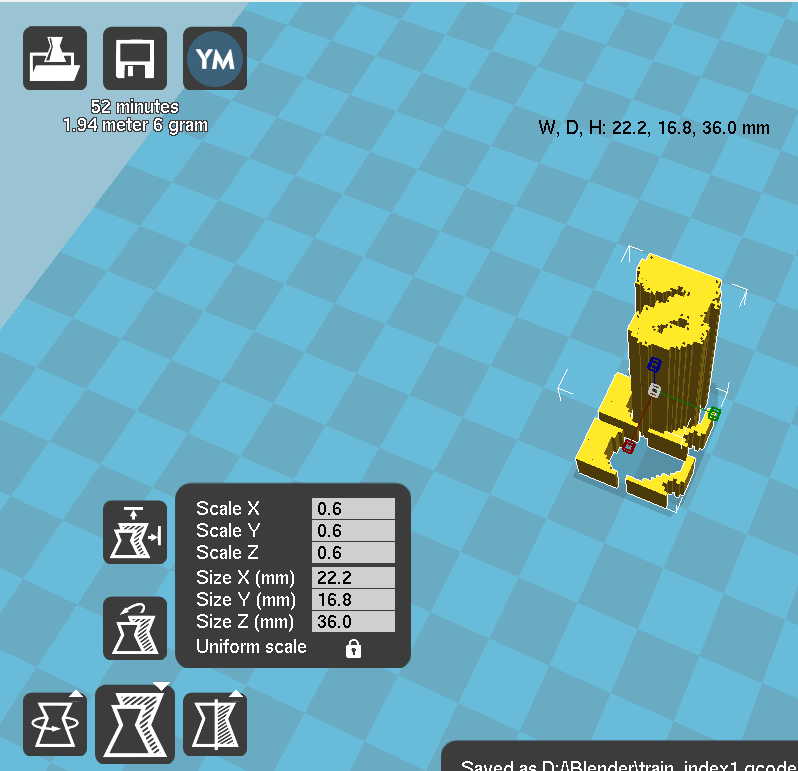
以下が 3Dプリンタ 用の Gcode (3Dプリンタのノズル制御命令) を生成する Cura というソフトの画面です。
元々全長が 60mm で作っていましたが、印刷時間が 3-4時間 と表示されたので、4割縮小して印刷しました。(Cura側で拡大縮小などのモデルの基本操作は行えるので、Blender ではスケールを気にしなくてもなんとかなります。)
6.2 印刷結果
左側が「0」、右側が「8」になります。
(「8」の土台が左右で分離してしまっていることにここで気付きました。)
(ひっくり返したら「8」が安定することに気付いた。)
こんな感じです。
6.3 耐久力
せっかくなので耐久テストもしてみましょう。
生半可なストレステストでは微動だにしなかったので、他に方法がないので最終的に自分の体重を全力でかけました。
データセットの「0」
生成した数字
どちらも折れてしまった…
(両方同時に体重をかけたら強い方が分かったかもしれないと後悔している。
一応 GAN の生成結果はランダムシードに沿ったものなので、再現することは容易ですが。)
断面を確認した所、どちらも 3Dプリンタ のフィラメントの積層面に沿って破断していました。
7. 結論
結論
- 断面二次モーメントを GAN のロスに加えることで、理論上の断面性能を上げることに成功
- この原理を逆に応用することで、強度の低い断面デザインも可能
- 断面二次モーメントは上げる場合も下げる場合も、FID とのトレードオフになる
- 最終的に、Blender を経由し 3Dプリンタ で印刷できることを確認
実験で得た新たな仮説
- 断面二次モーメントのロスを使い、レアデータを狙って生成することで、Few-Show Learning に使用するデータ拡張のための GAN に使えると考えた (これ誰か一緒にやりませんか)
- 断面二次モーメントが下がるようなロスをわずかにかけることで、 FID が改善するという仮説を立てた (これもd)
8. おわりに
今回は、わかりやすさと GAN の学習の複雑さを緩和するため、MNIST で試しましたが、他のデータでも理屈的には応用可能だと思います。
また、これらはバイアスがかかってしまうので、強度を操作しつつ目的の数字を出すには Conditional GAN などで条件付けさせて生成する必要があると思います。応用として、Conditional GAN の条件付けの部分に強度情報を与え、その強度に従った断面を生成する、ということも理屈的にはできるはずです。
最終的に、これらを応用し、FEM(=有限要素法) などを用いたり構造の力の釣り合いを計算し、ロスを加えることで、三次元の構造にも応用可能と考えています。(既にあったら教えて下さい)
nardtree さんがやっていた「StackGAN によるフォントの錬金術 9 」とも相性がかなり良いと考えています。
9. 謝辞
しちやさん(@sitiya78): 3Dプリンタは個人的に Amazon ほしいものリストで頂いたものです。この節は本当にありがとうございました。感謝してもしきれません。
10. 実験用コード
ここ: https://github.com/p-geon/DanmenGAN に全てを置いておきます。
-
Blender用コード: https://github.com/p-geon/DanmenGAN/blob/master/Blender/blender_mesh_generator.py
-
DanmenGAN 本体: https://github.com/p-geon/DanmenGAN/blob/master/Colaboratory/DanmenGAN.ipynb
-
統計値計算: https://github.com/p-geon/DanmenGAN/tree/master/calcstats
-
各種画像、重み、学習曲線、スコアなど:https://github.com/p-geon/DanmenGAN/tree/master/ExperimentalResults
Appendix
オマケ
A. TensorFlow のレイヤー構成について
TensorFlow 2.0 のレイヤー構成について説明します。
ざっくりと、Generator/Discriminator/Generator&Discriminator の三つについて解説します。マニア向け。
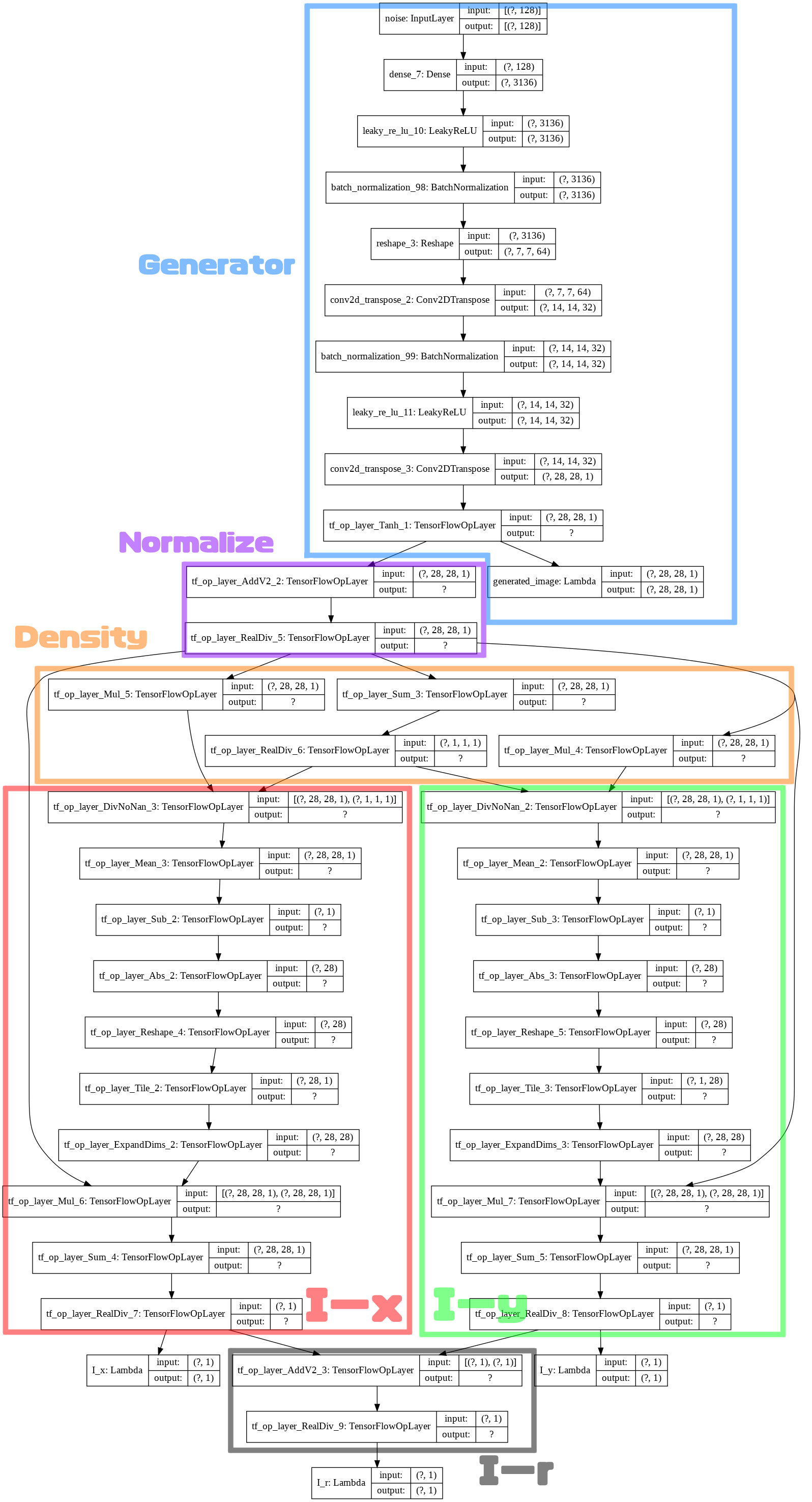
A-1. Generator
(画像クリックで詳細を確認できます。)
Generator は大まかに、画像を生成するグラフ(Generator)、正規化グラフ(Normalize)、密度を求めるグラフ(Density)、断面二次モーメント $I_x$ を求めるグラフ (I-x)、断面二次モーメント $I_y$ を求めるグラフ (I-y)、断面二次極モーメントを求めるグラフ $I_r$ (I-r) に分けて考えられます。
Generator: 画像生成グラフ〜正規化グラフ
以下に Generator の画像生成部〜正規化までのコードを書きます。
基本は通常の GAN と変わらないです。
また、GAN に関する情報はネット上にたくさんあるので、ここでは省きます。
smoa というのは断面二次モーメントを計算するためのクラスになり、この内部で密度計算〜断面二次モーメントの計算を行います。
def build_generator(params, smoa):
# Noise
z = z_in = tf.keras.layers.Input(shape=(params.NOISE_DIM, ), name="noise")
# (NOISE_DIM, ) -> (1024, )
x = tf.keras.layers.Dense(1024)(z)
x = tf.keras.layers.LeakyReLU(alpha=0.2)(x)
x = tf.keras.layers.BatchNormalization(momentum=0.8)(x)
# (1024, ) -> (7*7*64, ) -> (7, 7, 64)
x = tf.keras.layers.Dense(7*7*64)(z)
x = tf.keras.layers.LeakyReLU(alpha=0.2)(x)
x = tf.keras.layers.BatchNormalization(momentum=0.8)(x)
x = tf.keras.layers.Reshape(target_shape=(7, 7, 64))(x)
# (7, 7, 64) -> (14, 14, 32)
x = tf.keras.layers.Conv2DTranspose(32, kernel_size=(5, 5)
, padding='same', strides=(2, 2), use_bias=False, activation=None)(x)
x = tf.keras.layers.BatchNormalization(momentum=0.8)(x)
x = tf.keras.layers.LeakyReLU(alpha=0.2)(x)
# (14, 14, 128) -> (28, 28, 1)
x = tf.keras.layers.Conv2DTranspose(1, kernel_size=(5, 5)
, padding='same', strides=(2, 2), use_bias=False, activation=None)(x)
img = tf.math.tanh(x)
y = tf.keras.layers.Lambda(lambda x: x, name="generated_image")(img) # img は後ろで使うので y に変数名を変更しておく
"""
断面二次モーメントの計算 (ResNet みたいなグラフになる)
"""
# range: [-1.0, 1.0] -> [0.0, 1.0]
img = (img + 1.0)/2.0
I_x, I_y, I_r = smoa.calc_second_moment_of_area(img)
return tf.keras.Model(inputs=z_in, outputs=[y, I_x, I_y, I_r])
Generator: 密度計算グラフ〜断面二次モーメント計算グラフ
以下が、断面二次モーメントをテンソル演算のみで求めるグラフ構築法です。
まずは計算グラフで定数となるものを先に計算し、クラスの変数として tf.constant() を利用して先にテンソルを準備しておきます。
使用するのは、self.arange_x, self.arange_y, self.distance_matrix_x, self.distance_matrix_y, self.norm_I_x, self.norm_I_y です。
変数の説明としては、
-
self.arange_x/self.arange_y: シンプルに順番に並んでいるベクトル -
self.distance_matrix_x/self.distance_matrix_y: 軸からの距離を表すテンソル -
self.norm_I_x/self.norm_y: 正規化のための最大断面二次モーメント(スカラー)
となります。
class SecondMomentOfArea:
def __init__(self, img_shape=(28, 28)):
distance_vector_x = np.asarray([0.5+d for d in range(img_shape[1])])
distance_matrix_x = np.tile(distance_vector_x, (img_shape[0], 1))
distance_matrix_y = distance_matrix_x.T
"""
正規化用マトリックス
"""
matrix_for_norm_I_x = np.tile(np.abs(arange_y - img_shape[0]/2.0), (img_shape[1], 1)).T
norm_I_x = np.sum(matrix_for_norm_I_x)
matrix_for_norm_I_y = np.tile(np.abs(arange_x - img_shape[1]/2.0), (img_shape[0], 1)).T
norm_I_y = np.sum(matrix_for_norm_I_y)
"""
to TFconstant
"""
self.arange_x = tf.constant(arange_x, dtype=tf.float32) # (28, )
self.arange_y = tf.constant(arange_y, dtype=tf.float32) # (28,)
self.distance_matrix_x = tf.constant(distance_matrix_x[np.newaxis, :, :, np.newaxis], dtype=tf.float32) # (1, 28, 28, 1)
self.distance_matrix_y = tf.constant(distance_matrix_y[np.newaxis, :, :, np.newaxis], dtype=tf.float32) #(1, 28, 28, 1)
self.norm_I_x = tf.constant(norm_I_x, dtype=tf.float32) #()
self.norm_I_y = tf.constant(norm_I_y, dtype=tf.float32) #()
distance_matrix を正規化し、[0, :, :, 0] を切り抜き、図示すると、以下のようになっています。
| distance_matrix_x | distance_matrix_y |
|---|---|
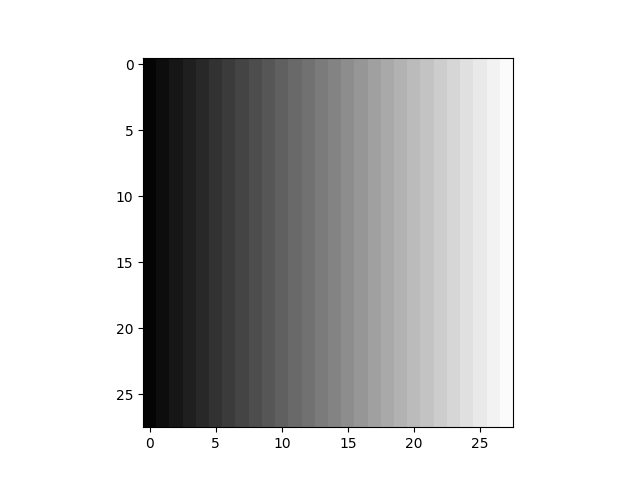 |
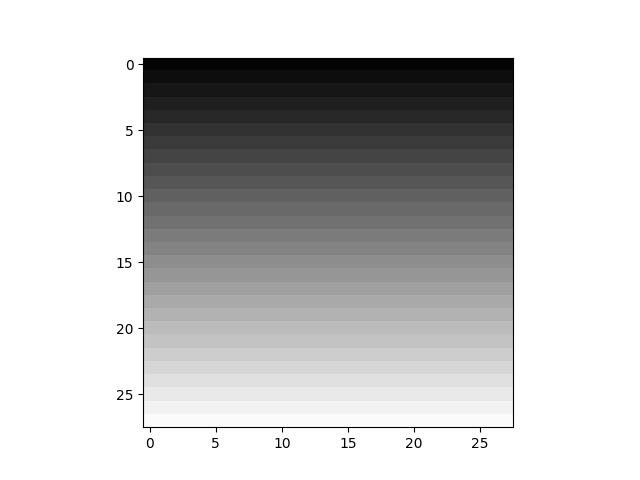 |
先程のクラスの続きを書きます。
断面二次モーメントを計算するためには、まず断面の重心(中立軸)を計算する必要があります。
そして、中立軸を計算するために密度 (全画素の合計/画像のピクセル数) を計算します。
まず、先程の distance_matrix と画像の画素値を要素ごとの掛け算にかけ、モーメントを求めます。次に、そのモーメントを密度を使って補正し、モーメントが均等なときは中立軸が画像の中心に来るようにした計算になります。
中立軸の計算が終わったら、中立軸に対する距離を表すテンソルを、引き算 → 絶対値 → 変形 → タイリング → 軸追加 という流れで作成します。
あとは、その距離を表すテンソルと画像を、要素ごとの掛け算で計算し、合計を求め、正規化すれば断面二次モーメントの計算が終わります。
断面極二次モーメント $I_r$ の計算は、定義通りに $I_x$ と $I_y$ を足し、最大が 1.0 になるよう正規化しておきます。
tf.keras.layers.Lambda(lambda x: x)(・) は何もしませんが、レイヤーの視認性を上げるために書いています。
def calc_second_moment_of_area(self, img): # (None, 28, 28, 1)
"""
中立軸の計算
"""
density = (tf.reduce_sum(img, axis=[1, 2], keepdims=True)/(img.shape[1]*img.shape[2]))
# (1, 28, 28, 1) x (None, 28, 28, 1) -> (None, 28, 28, 1)
x_moment = tf.math.divide_no_nan(tf.math.multiply(self.distance_matrix_x, img), density)
y_moment = tf.math.divide_no_nan(tf.math.multiply(self.distance_matrix_y, img), density)
# (None, 28, 28, 1) -> (None, )
neutral_axis_x = tf.math.reduce_mean(x_moment, axis=[1, 2])
neutral_axis_y = tf.math.reduce_mean(y_moment, axis=[1, 2])
"""
断面二次モーメント (縦)
I_x = ∫_A y^2 dA
"""
# sub: (None, 28, ) - (None, ) -> abs: (None, 28)
dy = tf.math.abs(self.arange_y - neutral_axis_y)
# (None, 28) -> (None, 1, 28)
dy = tf.reshape(dy, shape=[-1, img.shape[1], 1])
# (None, 1, 28) -> (None, 28, 28)
matrix_x = tf.tile(dy, multiples=[1, 1, img.shape[2]])
# (None, 28, 28) -> (None, 28, 28, 1)
matrix_x = tf.expand_dims(matrix_x, 3)
# (None, 28, 28, 1)x(None, 28, 28, 1) -> (None, 28, 28, 1) -> (None,)
I_x = tf.math.reduce_sum(tf.math.multiply(matrix_x, img), axis=[1, 2])/self.norm_I_x
"""
断面二次モーメント (横)
I_y = ∫_A x^2 dA
"""
# sub: (None, 28, ) - (None, ) -> abs: (None, 28)
dx = tf.math.abs(self.arange_x - neutral_axis_x)
# (None, 28) -> (None, 28, 1)
dx = tf.reshape(dx, shape=[-1, 1, img.shape[2]])
# (None, 1, 28) -> (None, 28, 28)
matrix_y = tf.tile(dx, multiples=[1, img.shape[1], 1])
# (None, 28, 28) -> (None, 28, 28, 1)
matrix_y = tf.expand_dims(matrix_y, 3)
# (None, 28, 28, 1)x(None, 28, 28, 1) -> (None, 28, 28, 1) -> (None,)
I_y = tf.math.reduce_sum(tf.math.multiply(matrix_y, img), axis=[1, 2])/self.norm_I_y
"""
断面二次極モーメント (正規化のため 2.0 で割る)
"""
I_r = (I_x + I_y)/2.0
"""
Lambda
"""
I_x = tf.keras.layers.Lambda(lambda x: x, name="I_x")(I_x)
I_y = tf.keras.layers.Lambda(lambda x: x, name="I_y")(I_y)
I_r = tf.keras.layers.Lambda(lambda x: x, name="I_z")(I_r)
return I_x, I_y, I_r
Blender 側で生成するときは、断面二次モーメントを計算する部分は必要ないので、適当な関数で (None, ) のテンソルを三つ出力すればいいです。
自分は、tf.reduce_sum(img) で処理しました。
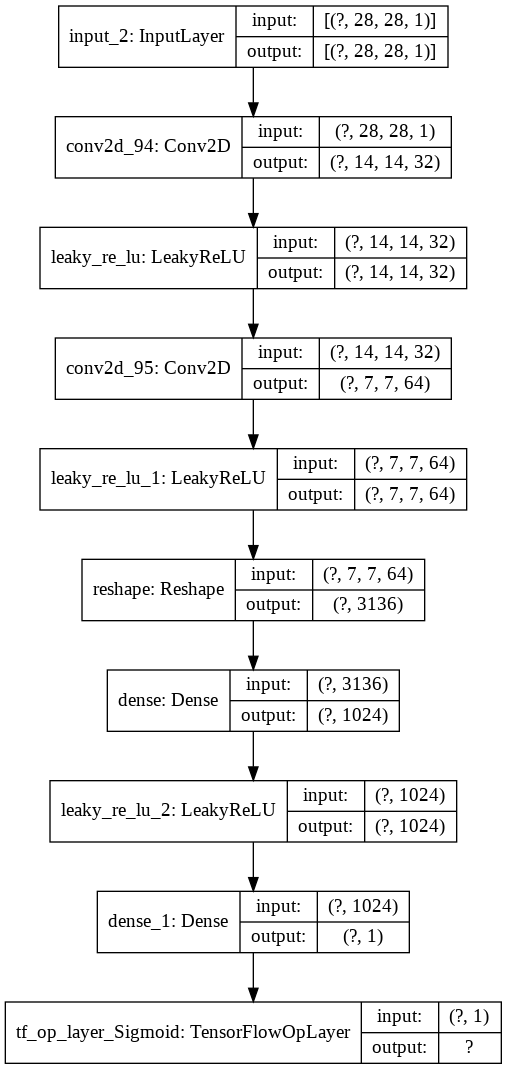
A-2. Discriminator
Discriminator は、通常の GAN と変わりません。古典的な DCGAN 風です。
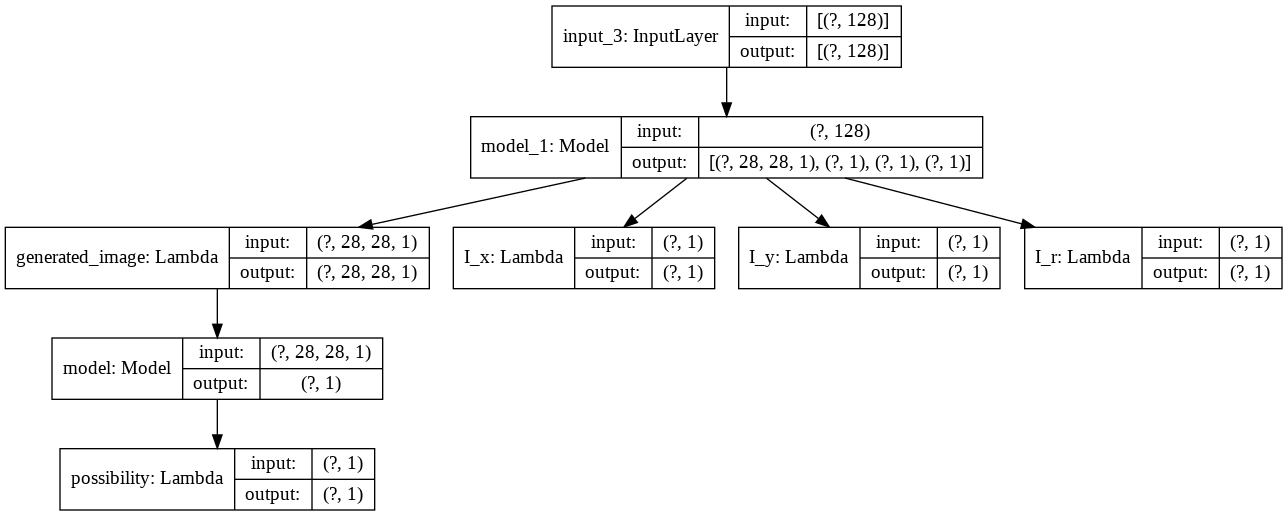
A-3. Generator & Discriminator
GAN の学習を行うために、Generator と Disctiminator を結合したグラフも作ります。
インプットは、ノイズ z のみ、アウトプットは、Discriminator によって出力された予測確率 p と I_x, I_y, I_r となります。
三種の断面二次モーメントは、計算するだけしておいて、ロスをかけるさいに係数を調整すればいいので、これで通常の GAN も学習できるし、断面二次モーメントを強化することもできます。断面二次モーメントを弱くしたい場合、$I$ の目標値を 1.0 から 0.0 に変更すれば済みます。
参考資料
主にこれを作るために書いた自分のメモなど
- tf.print() を使う時に f-string 内だとテンソルの中身が表示できない: https://qiita.com/HyperPigeon/items/007c5adca9a4e78bc6d1
- TensorFlow 2.0 の Frechet Inception Distance (FID) の計算の tf.linalg.sqrtm() で Nan が出るときの応急処置: https://qiita.com/HyperPigeon/items/f3f20f480269e2594724
- TensorFlow 2.0 で tf.keras.utils.plot_model() を使った時 AttributeError: 'dict' object has no attribute 'name' になるエラーとその解決法: https://qiita.com/HyperPigeon/items/fb22b555e76b52b3d688
- tensorflow_addons (tfa.image.rotate) で Colaboratory (Jupyter Notebook) のセッションがクラッシュするときの解決法: https://qiita.com/HyperPigeon/items/94831b8a9af75527b67b
- Blender 2.8 以降における寸法(メートルなど)表示法: https://qiita.com/HyperPigeon/items/c5d2ec3264e8fd14d167
- Blender 2.8.2 で TensorFlow 2.0(CPU) をインストールし、HelloWorld (Windows10): https://qiita.com/HyperPigeon/items/e6c37dc143039b75d0e4
-
Alec Radford, Luke Metz, Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. In ICLR 2016. ↩ ↩2
-
Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, Sepp Hochreiter. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In NIPS, 2017. ↩
-
LeCun, Yann and Cortes, Corinna. MNIST handwritten digit database, 2010. ↩ ↩2
-
Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair,Aaron Courville, and Yoshua Bengio. Generative Adversarial Networks. In NIPS, 2014. ↩ ↩2
-
http://www2.kyu-dent.ac.jp/depart/hoshasen/tf-2010/tf-2010/tf-aboutMRI.html ↩
-
https://github.com/p-geon/StealthFlow/blob/master/stealthflow/fid.py ↩