概要
クリスマスが終わっても寄稿できるようなので枠を頂きます。タイトルの通り周波数依存重み付きLQR(FWLQR: Frequency Weighted LQR)の紹介とJulia ControlSystems Toolboxhttps://github.com/JuliaControl/ControlSystems.jlを使ったシミュレーションをやってみます。
周波数依存重み付きLQRについて
問題設定
制御対象の状態方程式を
\frac{\mathrm{d}x(t)}{\mathrm{d}t}=Ax(t)+Bu(t)
としたとき、通常のLQRでは状態$x\in\mathbb{R}^{n}$ 、入力$u\in\mathbb{R}^{m}$ に対する評価関数を二次形式により
J=\int_{0}^{\infty}\left(x^{\top}(t)Qx(t)+u^{\top}(t)Ru(t)\right)\mathrm{d}t
と定めるのでした。ここに$Q\in\mathbb{R}^{n\times n}$、$R\in\mathbb{R}^{m\times m}$はそれぞれ状態、入力に対する重み付けのための行列です。
一方FWLQRにおいて評価関数は周波数領域において以下のように記述されます。
J=\frac{1}{2\pi}\int_{-\infty}^{\infty}\left(X^{*}(j\omega)Q^{*}(j\omega)Q(j\omega)X(j\omega)+U^{*}\left(R^{-1}(j\omega)\right)^{*}R^{-1}(j\omega)U(j\omega)\right)\mathrm{d}\omega
$X$、$U$はそれぞれ$x$、$u$のフーリエ変換であり、重みも伝達行列$Q$、$R^{-1}$の周波数特性として与えられています。なお、$(\cdot)^{*}$はエルミート転置を表します。
上式から分かるとおり、FWLQRでは伝達行列$Q$、$R^{-1}$の周波数特性により帯域ごとに異なる重みを設定できることがわかります。例えば$Q$にローパス特性、$R^{-1}$にハイパス特性を持たせた場合、低周波帯での低感度化と高周波帯でのロールオフによるロバスト化を指向した設計が行われることが期待できます。
解法
上記の評価関数において、$Q(j\omega)X(j\omega)$および$R^{-1}(j\omega)U(j\omega)$はそれぞれシステム$Q(s)$、$R^{-1}(s)$に入力$x(t)$、$u(t)$を与えた際の出力の周波数応答とみなすことができます。仮にこれを
\begin{aligned}
Y_{Q}(s)&=Q(s)X(s)\\
U_{R}(s)&=R^{-1}(s)U(s), U(s)=R(s)U_{R}(s)
\end{aligned}
と表し、$Q(s)$、$R(s)$の状態空間表現を
Q(s):\left\{
\begin{aligned}
\frac{\mathrm{d}x_{Q}(t)}{\mathrm{d}t}&=A_{Q}x_{Q}(t)+B_{Q}x(t)\\
y_{Q}(t)&=C_{Q}x_{Q}(t)+D_{Q}x(t)
\end{aligned}
\right.\\
R(s):\left\{
\begin{aligned}
\frac{\mathrm{d}x_{R}(t)}{\mathrm{d}t}&=A_{R}x_{R}(t)+B_{R}u_{R}(t)\\
u(t)&=C_{R}x_{R}(t)+D_{R}u_{R}(t)
\end{aligned}
\right.
と与えた場合、評価関数は
\begin{aligned}
J&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\left(Y^{*}_{Q}(j\omega)Y_{Q}(j\omega)+U_{R}^{*}(j\omega)U_{R}(j\omega)\right)\mathrm{d}\omega\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\left(X^{*}(j\omega)D_{Q}^{\top}D_{Q}X(j\omega)+X^{*}_{Q}(j\omega)C_{Q}^{\top}C_{Q}X_{Q}(j\omega)+U_{R}^{*}(j\omega)U_{R}(j\omega)\right)\mathrm{d}\omega
\end{aligned}
と変形できます。そしてここが本手法の面白い点なのですが、この評価関数にパーセバルの定理
\int_{-\infty}^{\infty}f^{\top}(t)f(t)\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{\infty}F^{*}(j\omega)F(j\omega)\mathrm{d}\omega
を適用すると、再び時間領域の評価関数
J=\int_{-\infty}^{\infty}\left(x^{\top}(t)D_{Q}^{\top}D_{Q}x(t)+x^{\top}_{Q}(t)C_{Q}^{\top}C_{Q}x_{Q}(t)+u_{R}^{\top}(t)u_{R}(t)\right)\mathrm{d}t
を得ることができます。この結果はFWLQRの設計問題が制御対象の入出力にフィルタ$R(s)$、$Q(s)$を付与した下図の拡大系のLQR設計問題に帰着できることを示しています。
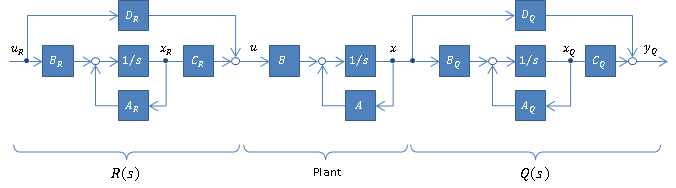
仮に拡大系の状態変数を
\xi:=\left[
\begin{array}{c}
x\\x_{Q}\\x_{R}
\end{array}
\right]
と定義したとき、状態方程式は
\frac{\mathrm{d}\xi(t)}{\mathrm{d}t}=\left[
\begin{array}{ccc}
A&0&BC_{R}\\
B_{Q}&A_{Q}&0\\
0&0&A_{R}
\end{array}
\right]\xi(t)+\left[
\begin{array}{c}
BD_{R}\\0\\B_{R}
\end{array}
\right]u_{R}(t)
となり、状態重みと入力重みをそれぞれ
\left[
\begin{array}{ccc}
D_{Q}^{\top}D_{Q}&0&0\\
0&C_{Q}^{\top}C_{Q}&0\\
0&0&0
\end{array}
\right], I
とおいたLQRを解くことでFWLQRの状態フィードバックゲインが求まります。
Juliaによるシミュレーション
JuliaにMATLABライクな制御系設計機能を付与するツールボックスControlSystems Toolboxが提供されていましたので、今回はこれを使ってシミュレーションを行います。関数もlqr、ssなどMATLABで見慣れたものばかりですのであまり抵抗なく使用できると思います。
例題
せっかく周波数特性を設計に盛り込めるので、モデル化誤差に対するロバスト制御問題についてLQRとFWLQRを比較してみましょう。以下では慣性モーメント$J_{L}$の負荷と$J_{M}$のモータ間での回転運動の伝達を考えます。負荷の角度$\theta_{L}$および角速度$\omega_{L}$を状態変数、入力を動力側のトルク$\tau$にとり、回転軸が剛体であると仮定した場合、この系の状態空間表現は
P_{n}(s):\left\{
\begin{aligned}
\frac{\mathrm{d}}{\mathrm{d}t}\left[
\begin{array}{c}
\theta_{L}(t)\\\omega_{L}(t)
\end{array}
\right]&=\left[
\begin{array}{cc}
0&1\\
0&0
\end{array}
\right]\left[
\begin{array}{c}
\theta_{L}(t)\\\omega_{L}(t)
\end{array}
\right]+\left[
\begin{array}{c}
0\\1/(J_{L}+J_{M})
\end{array}
\right]\tau(t)\\
&=:A_{n}\xi_{n}(t)+B_{n}\tau(t)\\
y(t)&=\left[
\begin{array}{cc}
1&0\\
0&1
\end{array}
\right]\left[
\begin{array}{c}
\theta_{L}(t)\\\omega_{L}(t)
\end{array}
\right]\\
&=:C_{n}\xi_{n}(t)+D_{n}\tau(t)
\end{aligned}
\right.
と表せます。一方回転軸が剛体でなく、弾性$K$、抵抗$C$を持つ場合、動力側の回転角度$\theta_{M}$、角速度$\omega_{M}$を状態変数に加えた状態空間表現は
P(s):\left\{
\begin{aligned}
\frac{\mathrm{d}}{\mathrm{d}t}\left[
\begin{array}{c}
\theta_{L}(t)\\\theta_{M}(t)\\\omega_{L}(t)\\\omega_{M}(t)
\end{array}
\right]&=\left[
\begin{array}{cc}
0&0&1&0\\
0&0&0&1\\
-K/J_{L}&K/J_{L}&-C/J_{L}&C/J_{L}\\
K/J_{M}&-K/J_{M}&C/J_{M}&C/J_{M}
\end{array}
\right]\left[
\begin{array}{c}
\theta_{L}(t)\\\theta_{M}(t)\\\omega_{L}(t)\\\omega_{M}(t)
\end{array}
\right]+\left[
\begin{array}{c}
0\\0\\0\\1/J_{M}
\end{array}
\right]\tau(t)\\
&=:A\xi(t)+B\tau(t)\\
y(t)&=\left[
\begin{array}{cc}
1&0&0&0\\
0&0&1&0
\end{array}
\right]\left[
\begin{array}{c}
\theta_{L}(t)\\\theta_{M}(t)\\\omega_{L}(t)\\\omega_{M}(t)
\end{array}
\right]\\
&=C\xi(t)+D\tau(t)
\end{aligned}
\right.
となります。以後、$P_{n}$をノミナルプラント、$P$を厳密プラントとして設計します。$J_{L}=J_{M}=1,K=1,C=0.5$として、まずは両者の周波数応答を比較しましょう。Julia ControlSystems Toolboxでは以下のコードで解析することができます。
using PyPlot;
using ControlSystems;
JL = 1; JM = 1;
K = 1;
C = 0.5;
An = [0 1;0 0];
Bn = [0;1/(JL+JM)];
Cn = [1 0];
Dn = 0;
A = [
0 0 1 0;
0 0 0 1;
-K/JL K/JL -C/JL C/JL;
K/JM -K/JM C/JM -C/JM
];
B = [
0;0;0;1/JM
];
C = [
1 0 0 0;
];
D = 0;
Pn = ss(An,Bn,Cn,Dn);
P = ss(A, B, C, D);
w = logspace(-2,1,10000);
F = bode([P;Pn], w);
PyPlot.xscale("log");
PyPlot.plot(w, 20*log10.(F[1][:,:,1]));
PyPlot.xlabel("frequency [rad/s]");
PyPlot.ylabel("gain [dB]");
PyPlot.legend(["strict", "nominal"]);
PyPlot.grid(true);
PyPlot.show();
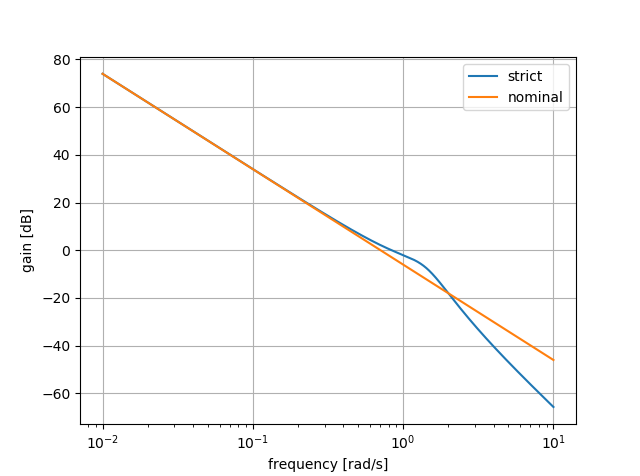
とまぁ、モジュール読み込み以外はMATLABと同じように書けます。実行すると以下のプロットが出力されます。厳密プラント(青線)には回転軸の弾性に伴う遅れが生じています。
設計
まずはノミナルプラントに対してLQRを設計しましょう。センサ出力から全状態が得られるためオブザーバは必要ありません。重み行列を
Q=\left[
\begin{array}{cc}
1&0\\0&9
\end{array}
\right]
,R=1
とおき、$A_{n},B_{n},Q,R$から得られた最適状態フィードバックゲインを$k_{LQR}$とします。厳密プラントに対しては負荷回転角$\theta_{L}$と角速度$\omega_{L}$を出力と定義したため、$k_{LQR}$によるフィードバックシステムは
\frac{\mathrm{d}\xi(t)}{\mathrm{d}t}=\left(A-Bk_{LQR}C\right)\xi(t)+B\tau(t)
となります。以下のスクリプトで$\theta_{L}(0)=1$に対する初期値応答をシミュレーションします。
using PyPlot;
using ControlSystems;
t = 0:0.01:20;
JL = 1; JM = 1;
K = 1;
C = 0.5;
An = [0 1;0 0];
Bn = [0;1/(JL+JM)];
Cn = [1 0;0 1];
Dn = [0;0];
A = [
0 0 1 0;
0 0 0 1;
-K/JL K/JL -C/JL C/JL;
K/JM -K/JM C/JM -C/JM
];
B = [
0;0;0;1/JM
];
C = [
1 0 0 0;
0 0 1 0
];
D = [0;0];
Q = [1 0;0 9];
R = 1;
klqr = lqr(An, Bn, Q, R);
Gcln = ss(An-Bn*klqr, Bn, Cn, Dn);
Gcl = ss(A-B*klqr*C, B, C, D);
u = zeros(size(t));
yn = lsim(Gcln, u, t, [1;0]);
y = lsim(Gcl, u, t, [1;0;0;0]);
PyPlot.plot(t, y[1][:,1], t, yn[1][:,1]);
PyPlot.xlabel("time [s]");
PyPlot.ylabel("angle [deg]");
PyPlot.legend(["strict", "nominal"]);
PyPlot.show();
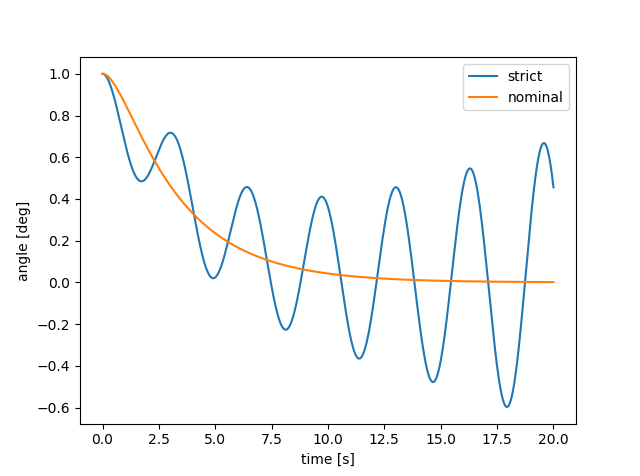
ControlSystems Toolboxには初期値応答を求める関数がないため入力0のlsimにて求めていますが、制御系設計もほぼMATLABと変わらない記述で行えることがわかります。このスクリプトを実行すると以下のプロットが出力されます。ノミナルプラントに対するシミュレーションでは負荷回転角は速やかに収束しますが、厳密プラントに対するシミュレーションではモデル化誤差の影響により不安定化しています。
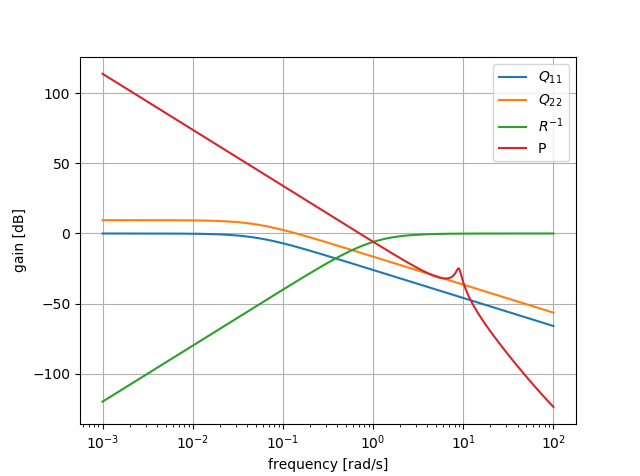
次にFWLQRを設計します。ノミナルプラントと厳密プラントの誤差が小さい低周波帯域では状態変数に関する重みを大きくし、モデル化誤差の影響が顕著な高周波帯域では制御入力に関する重みを大きくします。ここでは
Q(s)=\left[
\begin{array}{cc}
\frac{1}{1+s/0.05}&0\\
0&\frac{3}{1+s/0.05}
\end{array}
\right],R^{-1}(s)=\left(\frac{s}{1+s}\right)^{2}
以上の設定のもと、FWLQRを設計し$\theta_{L}=1$に対しシミュレーションを行うスクリプトは次のとおりです。
using PyPlot;
using ControlSystems;
t = 0:0.01:40;
JL = 1; JM = 1;
K = 1;
C = 0.5;
An = [0 1;0 0];
Bn = [0;1/(JL+JM)];
Cn = [1 0;0 1];
Dn = [0;0];
nn = size(An,1);
A = [
0 0 1 0;
0 0 0 1;
-K/JL K/JL -C/JL C/JL;
K/JM -K/JM C/JM -C/JM
];
B = [
0;0;0;1/JM
];
C = [
1 0 0 0;
0 0 1 0
];
D = [0;0];
n = size(A,1);
Aq = diagm([0.05, 0.05]);
Bq = diagm([0.05, 0.05]);
Cq = diagm([1, 3]);
Dq = [0 0;0 0];
nq = size(Aq,1);
Ar = [0 1;0 0];
Br = [0;1];
Cr = [1 1];
Dr = 1;
nr = size(Ar,1);
Aen = [
An zeros(nn,nq) Bn*Cr;
Bq Aq zeros(nq,nr);
zeros(nr,nn+nq) Ar
];
Ben = [
Bn*Dr;zeros(nq,1);Br
];
Cen = [eye(nn) zeros(nn,nq) zeros(nn,nr)];
Den = zeros(nn,1);
Qen = [
Dq'*Dq zeros(nn, nq+nr);
zeros(nq, nn) Cq'*Cq zeros(nq,nr);
zeros(nr, nn+nq+nr)
];
Ren = 1;
kfw = lqr(Aen,Ben,Qen,Ren);
Ae = [
A zeros(n,nq) B*Cr;
Bq*C Aq zeros(nq,nr);
zeros(nr,n+nq) Ar
];
Be = [
B*Dr;zeros(nq,1);Br
];
Ce = [
[1 0 0 0;0 0 1 0] zeros(nn,nq) zeros(nn,nr)
zeros(nq+nr,n) eye(nq+nr)
];
De = zeros(nn+nq+nr,1);
Gcln = ss(Aen-Ben*kfw, Ben, Cen, Den);
Gcl = ss(Ae-Be*kfw*Ce, Be, Ce, De);
u = zeros(size(t));
yn = lsim(Gcln, u, t, [1;0;zeros(nq+nr,1)]);
y = lsim(Gcl, u, t, [1;0;0;0;zeros(nq+nr,1)]);
PyPlot.plot(t, y[1][:,1], t, yn[1][:,1]);
PyPlot.xlabel("time [s]");
PyPlot.ylabel("angle [deg]");
PyPlot.legend(["strict", "nominal"]);
PyPlot.show();
シミュレーション結果は次のプロットのようになりました。
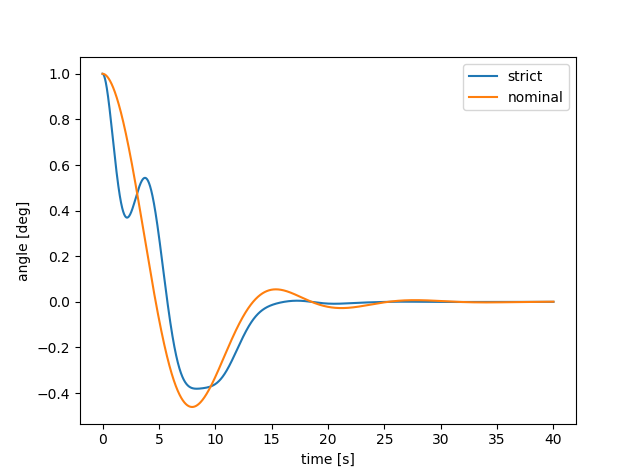
高周波帯のロールオフを導入したことでややアンダーシュートが発生していますが、厳密プラントに対しても安定化が行われています。
まとめ
周波数領域で定義された二次評価関数を最小化するFWLQRを紹介しました。FWLQR問題は、パーセバルの定理により評価関数を時間領域に変換することで、フィルタを導入したLQR問題に帰着できます。
本手法はモデル化誤差の大きい帯域で制御入力に強い重みを掛けることでロバスト性を向上できますが、$\mathcal{H}_{\infty}$制御における小ゲイン定理のようなロバスト安定性を保証できない点については注意が必要です。
また今回シミュレーションにJuliaを使用しました。MATLABユーザーであればほぼ問題なく使用できるでしょう。今回はJuliaの特徴であるJITコンパイラの恩恵を受けるような規模でもないためあまり速さを実感できませんでしたが、ゴリゴリループを回すような状況では威力を発揮するのでしょう(MATLABとの比較をどなたか・・・)。ControlSystems Toolboxもほぼ問題なく使えるのですが、一部プロット系の関数で修飾に難があったりとまだまだ開発途上という印象です。今後に期待したいと思います。