この記事中の全ての間違いは筆者の責任であり、所属する団体や組織を代表するものではありません。
はじめに
この記事は、量子力学を習いたての学部生にむけて、物性物理の魅力を存分に感じてほしいという思いで、「量子ホール効果」「トポロジカル物質」に焦点を当てて作成しました。この記事を通して、物性物理の魅力を再発見していただければ幸いです。
量子ホール効果の発見
「物性物理」と聞くと、まず最初に思い浮かぶのはどのような物理現象でしょうか?
最も馴染み深い現象は、金属中の電子の電気伝導現象(Drude理論)ではないでしょうか。これは高校の教育課程でも扱う基本的なモデルで、次のようなものでした。
Drude理論における仮定
$$
m\frac{d\boldsymbol{v}}{dt} = -e\boldsymbol{E}
-\frac{m\boldsymbol{v}}{\tau}
$$
$m,-e$は電子の質量と電荷、$\boldsymbol{E}$は外部電場です。右辺2項目は電子がイオン核に衝突して散乱することによる摩擦項です。$\tau$は散乱時間と呼ばれるもので、衝突の間の平均時間と考えることができます。今は平衡状態に興味があるので、$d\boldsymbol{v}/dt=0$ のときを考えることにしましょう。電流密度は電子密度$n$を用いて$\boldsymbol{J}=-ne\boldsymbol{v}$と書けることを思い出すと、この運動方程式の各成分は独立なので、
$$
\boldsymbol{E} = \rho_{DC} ~ \boldsymbol{J} , \quad \rho_{DC} = \frac{m}{e^2n\tau}
$$
のように、簡単に解くことができます。この式は、電流と電場の向きが等しく、さらに比例していることを示しています。では、ここに磁場を加えるとどうなるでしょうか?磁場中の電子はローレンツ力を受けてらせん運動(2次元系だと円運動)することを思い出すと、単純に電場と電流が比例するといった結果は得られないことが期待されます。実際に運動方程式を立てると、
$$
m\frac{d\boldsymbol{v}}{dt} = -e\boldsymbol{E}-e\boldsymbol{v}\times\boldsymbol{B}
-\frac{m\boldsymbol{v}}{\tau}
$$
のように書かれます。以降、2次元の自由電子系を考えることにして、$d\boldsymbol{v}/dt=0$、磁場を$\boldsymbol{B}=B\boldsymbol{e}_z$として代入すると、
\boldsymbol{E} = \hat{\rho} ~\boldsymbol{J}, \quad \hat{\rho} =
\begin{pmatrix}
\rho_{xx} & \rho_{xy} \\
\rho_{yx} & \rho_{yy}
\end{pmatrix}
=\rho_{DC}
\begin{pmatrix}
1 & \omega_B \tau \\
-\omega_B \tau & 1
\end{pmatrix}
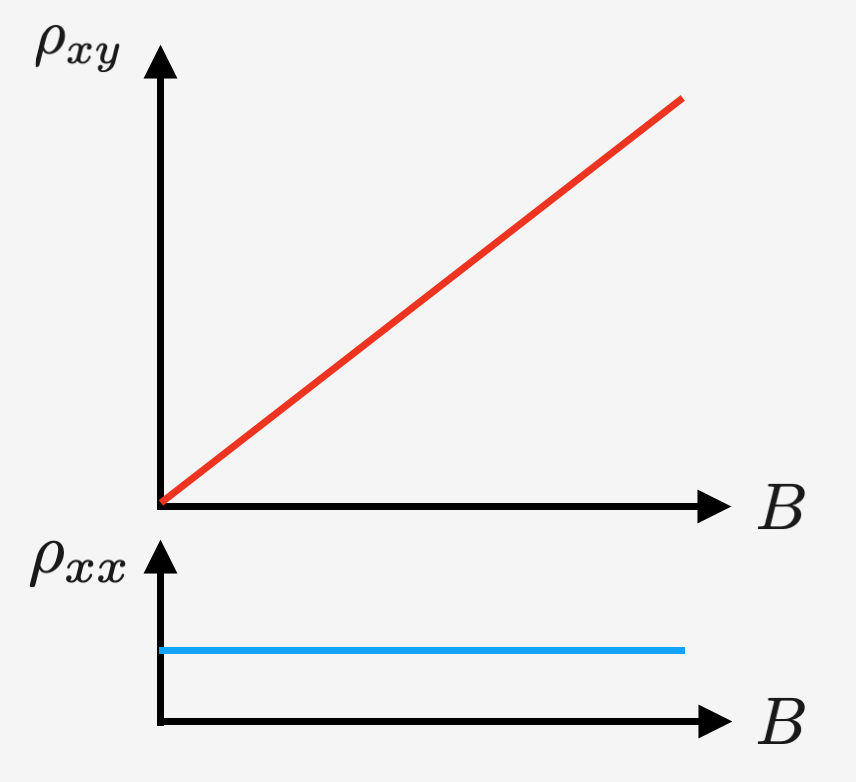
が得られます。ここで $\omega_B=eB/m$ はサイクロトロン振動数です。このように、磁場のある2次元自由電子系では電流と電場が比例せず、$\rho_{xy}$ のような非対角項が現れます3。$\rho_{xy}$はホール抵抗率と呼ばれる物理量で、$y$方向に電場をかけたときの$x$方向の電気抵抗率を表しています。いま、$\rho_{xx}=m/e^2n\tau,~~\rho_{xy}=B/ne$ と計算することができたので、磁場依存性は下図のようになることが予想できます。
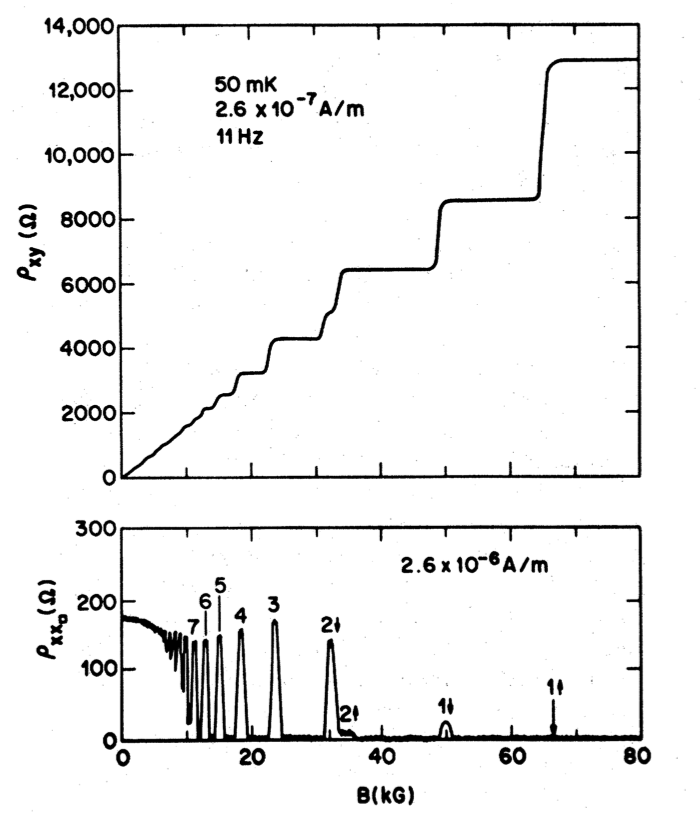
ところが、実際の実験結果は下図4のような結果になることが1980年に報告されました5。このとき測定されたホール抵抗率は、
$$
\rho_{xy} = \frac{2\pi\hbar}{e^2}\frac{1}{\nu}, \quad \nu \in \mathbb{Z}
$$
のように量子化され、なんと、その比例係数には基本定数の比が現れています。しかも、このように量子化されているときの縦抵抗は$\rho_{xx}=0$のように特異な振る舞いを示すという驚きの結果です!このように、古典的な運動方程式からは全く予想できない結果が得られたということは、比例係数にプランク定数が現れていることから分かるように、純粋に量子力学的な効果が現れているのです!
磁場中の量子力学
ホール抵抗の量子化を理解するために、まずは、磁場を正準量子化の手続きにしたがって量子力学に取り込むことを考えましょう。解析力学を復習すると、磁場下のラグランジアンは
$$
L = \frac{m}{2}\dot{\boldsymbol{x}}^2 -e\dot{\boldsymbol{x}}\cdot\boldsymbol{A}
$$
と書けるのでした。このラグランジアンの正準運動量は、$\boldsymbol{p}=\frac{\partial L}{\partial \dot{\boldsymbol{x}}}=m\dot{\boldsymbol{x}}-e\boldsymbol{A}$と計算できるので、ハミルトニアンは
$$
H = \dot{\boldsymbol{x}}\cdot\boldsymbol{p}-L=\frac{1}{2m}(\boldsymbol{p}+e\boldsymbol{A})^2
$$
と書き表すことができます6。次に、正準量子化の手続きにしたがって量子化することを考えましょう。つまり $m\dot{\boldsymbol{x}}\rightarrow-i\hbar\boldsymbol{\nabla}$ のように置き換えて、
$$
[x_i,p_j]=i\hbar \delta_{ij} \quad \text{with} \quad [x_i, x_j]=[p_i, p_j]=0
$$
という正準交換関係が満たされるようにします。以下では2次元の電子系を考えることにして、磁場は$xy$平面に対して垂直 $\boldsymbol{\nabla}\times\boldsymbol{A}=B\boldsymbol{e}_z$ にかけます。
ここでの正準運動量は $\boldsymbol{p}=m\dot{\boldsymbol{x}}-e\boldsymbol{A}$ でゲージ不変でない。つまり、ベクトルポテンシャル$\boldsymbol{A}$のゲージの取り方によって変わってしまい、物理的意味を持たない。
一方で、$m\dot{\boldsymbol{x}}$ はゲージ不変な物理量です。これを正準運動量 $\boldsymbol{p}$ と区別して、動的運動量 $\boldsymbol{\pi}\equiv\boldsymbol{p}+e\boldsymbol{A} = m\dot{\boldsymbol{x}}$ と呼ぶことにします。動的運動量のポアソンブラケットは
$$
\lbrace \pi_i, \pi_j \rbrace = \lbrace p_i+eA_i,p_j+eA_j \rbrace = -e\left(\frac{\partial A_j}{\partial x^i}-\frac{\partial A_i}{\partial x^j}\right) = -e\epsilon_{ijk}B_k
$$
のように交換しないので、量子化した後でも
$$
[\pi_x,\pi_y]=-ie\hbar B
$$
のように交換しないことに注意が必要です。
Landau準位
動的運動量を用いて、磁場中のハミルトニアンは
$$
H=\frac{(\boldsymbol{p}+e\boldsymbol{A})^2}{2m}=\frac{\boldsymbol{\pi}^2}{2m}
$$
のように書き換えることができます。ここで新たに
$$
a=\frac{1}{\sqrt{2e\hbar B}}(\pi_x-i\pi_y), \quad a^{\dagger} =\frac{1}{\sqrt{2e\hbar B}}(\pi_x+i\pi_y)
$$
のような演算子を定義すると、ハミルトニアンは
$$
H=\hbar \omega_B\left(a^{\dagger}a+\frac{1}{2}\right)
$$
のように表すことができ、$[a,a^{\dagger}]=1$という交換関係があることも分かります。もうお気づきの方もいると思いますが、これは1次元の調和振動子と同じ形になっています。すなわち、 $a^{\dagger},a$は生成消滅演算子であり、エネルギー固有値は
$$
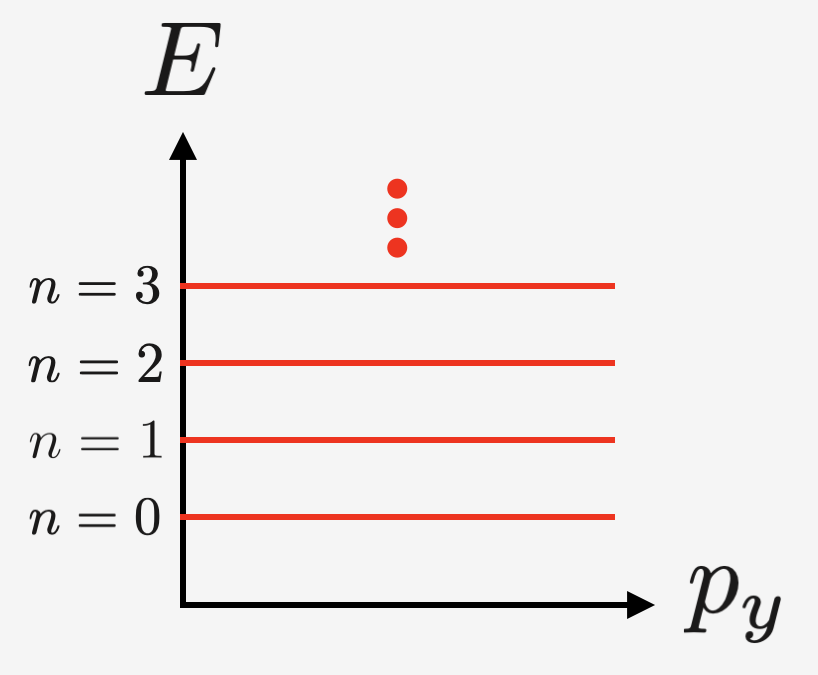
E_n = \hbar \omega_B\left(n+\frac{1}{2}\right) \quad \quad n \in \mathbb{N}
$$
のようになります。これをLandau準位と呼びます。
1次元調和振動子と完全に一致しているわけでは無いことに注意。振動数$\omega$の違いだけでなく、各準位にエネルギーの"縮退"が起きている。
縮退があることを確認するために、具体的にゲージを固定して考えることにしましょう。ここでは次のようなランダウゲージを選びます。
$$
\boldsymbol{A} = xB\boldsymbol{e}_{y}
$$
確かにこのとき $\boldsymbol{\nabla}\times\boldsymbol{A}=B\boldsymbol{e}_{z}$ が成り立っています。このときのハミルトニアンは、
$$
H=\frac{p_x^2+(p_y+eBx)^2}{2m}
$$
のようになっており、$y$ 方向の並進に対して不変であることが分かります。すなわち、$y$方向の運動量と $[H,p_y]=0$ のような交換関係があり、$y$方向の運動量が保存しているのです。このことから、各ランダウ準位には$y$方向の運動量量子数が異なる状態が縮退していることが分かりました。そもそも、2次元の量子状態が1次元の調和振動子と対応するわけですから、縮退が起きていることは当然の結果だったのです。
エッジ状態による説明
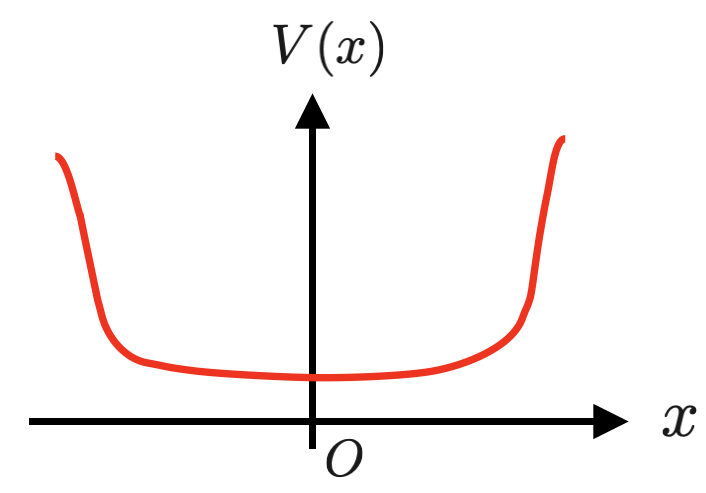
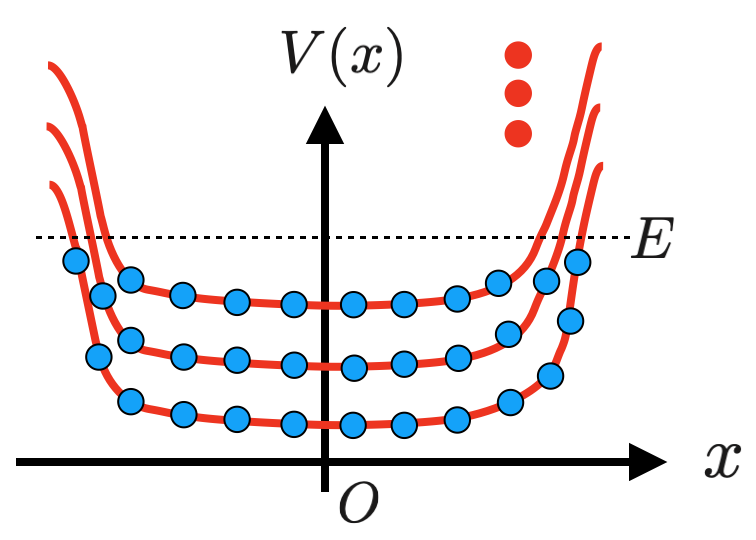
実はホール抵抗の量子化は、エッジ状態を使って説明することができます。$x$方向には有限の大きさ$L_x$を持ち、$y$方向には無限に長いような系を考えることにします。このとき、電子の感じるポテンシャルは、電子が系の外に逃げ出さないように下図のようになっているはずです。
このエッジポテンシャルをある位置$X$のまわりで展開すると
$$
V(x)\simeq V(X) + \frac{\partial V}{\partial x} (x-X) + \cdots
$$
のようになります。2次以上の項を無視する近似のもとで、ハミルトニアンは
$$
H=\frac{p_x^2+(p_y+eBx)^2}{2m} + \frac{\partial V}{\partial x} (x-X) + V(X)
$$
のように書けるので、$y$方向の運動量を $p_y \rightarrow \hbar k$ のようにすると、エネルギー分散は
$$
E_{n,k} = \hbar\omega_B\left(n+\frac{1}{2}\right) - \frac{\partial V}{\partial x} \left(kl_B^2+\frac{1}{m\omega_B^2}\frac{\partial V}{\partial x}\right)+\text{const.}
$$
のように計算できます。ここで、$l_B\equiv \sqrt{\hbar/eB}$は磁気長と呼ばれる量です。したがって、$y$方向の電子の速度は
$$
v_y = \frac{1}{\hbar}\frac{\partial E_{n,k}}{\partial k} = -\frac{1}{eB}\frac{\partial V}{\partial x}
$$
のように計算することができます。これから、$y$方向の電流も計算することができて、
$$
I_y = -e\int_{L_x/l_B^2}^{0}\frac{dk}{2\pi}v_y(k)=\frac{e}{2\pi l_B^2}\int_{0}^{L_x}dx \frac{1}{eB}\frac{\partial V}{\partial x} = \frac{e}{2\pi\hbar}\Delta\mu
$$
という結果が得られます。ここでホール電圧と $eV_H = \Delta \mu$ のような関係があるので、ホール抵抗は
$$
\rho_{xy} = \frac{V_H}{I_y} = \frac{2\pi\hbar}{e^2}
$$
という計算できます。今はただ一つのランダウ準位だけを考えていましたが、複数のランダウ準位が占有されている状況を考えると、たとえば $n$ 準位が占有されているとき、
$$
\rho_{xy} = \frac{2\pi\hbar}{e^2}\frac{1}{\nu}, \quad \nu \in \mathbb{Z}
$$
のようになります!つまり、これで実験結果を説明することができました。
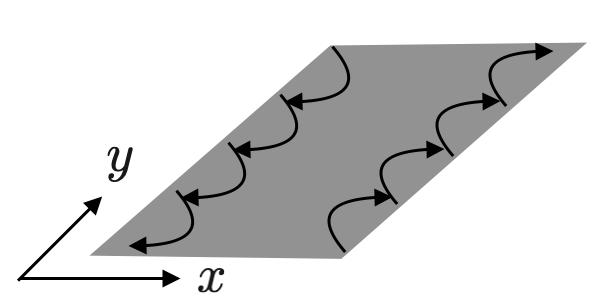
古典的な描像では、電子のサイクロトロン運動によって下図のように電流が流れていると解釈できます。
バルク・エッジ対応
前節までで、物質のエッジに着目すればホール抵抗の量子化を説明できることがわかりました。実は、エッジの性質はバルク(物質の内部)のトポロジカルな性質によって決まっていることが近年わかってきました。いわゆる、バルク・エッジ対応です。このような性質を持つ物質はトポロジカル物質と呼ばれていいます。このことを理解するために、やや天下り的ですが、ホール抵抗の量子化をバルクの性質だけから導いてみましょう。
まず、この系を特徴づけるパラメータとして、$\theta_i = 2\pi\Phi_i/\Phi_0~~~(i=x,y)$ を導入します。とくに $\Phi_0=2\pi\hbar/e$ は磁束量子とよばれる物理量です。このとき、$0 \le \theta_i < 2\pi$ という条件を課しておきます。
次に、Berry接続と呼ばれる
$$
A_i (\Phi) = -i\bra{\psi_0}\frac{\partial}{\partial\theta_i}\ket{\psi_0}
$$
を定義して、Berry曲率
$$
F_{xy} = \frac{\partial A_x}{\partial \theta_y}-\frac{\partial A_y}{\partial \theta_x}
$$
を定義します。このBerry曲率と呼ばれる量は、久保公式によってホール伝導率と次のような関係があります。(久保公式の説明は少し難しいので、ここでは公式だと思って先にすすんでください)
$$
\sigma_{xy} = \frac{e^2}{\hbar}\int \frac{d^2\theta}{(2\pi)^2}F_{xy}
$$
ここで、(第一)Chern数と呼ばれる量が
$$
C =\frac{1}{2\pi}\int \frac{d^2\theta}{(2\pi)^2}F_{xy}
$$
で与えられ、これは整数値しか取らないという数学の定理を用いると、
$$
\rho_{xy} = \sigma_{xy}^{-1} = \frac{2\pi\hbar}{e^2}\frac{1}{C} \quad \text{where} \quad C \in \mathbb{Z}
$$
という結果が得られます。この式は発見者にちなんでTKNN公式とよばれていて、2016年のノーベル物理学賞の受賞理由の一つです。
トポロジカル物質の例
ここまで、量子ホール効果(特に整数量子ホール効果)を扱ってきましたが、似たようなトポロジカルな量は、ランダウ準位のように各バンドの間にギャップ(バンド間の交差がない)がある系でも適応できるはずです。このことから発見されたのが、いわゆるトポロジカル絶縁体やトポロジカル超伝導体 などの物質群です。このような物質では、多体効果によって相対論的な電子(Dirac電子)や、Majorana粒子などが発現するなど、おもしろい物理が広がっています。量子ホール効果に限っても、電子間の相互作用が強くなると、分数量子ホール効果が起き、分数倍の電荷と磁束を持ったエニオンといった粒子が現れます。ぜひ、一緒に物性物理を研究しませんか?!
参考文献
- David Tong "The Quantum Hall Effect" (2016)
この記事の執筆全般において参考にさせていただきました。 - 吉岡大二郎「量子ホール効果」(1998)
トポロジカルな側面が発見される直前くらいに書かれた本 - 野村健太郎「トポロジカル絶縁体・超伝導体」(2016)
トポロジカルな側面に焦点を当てた現代的な本 - 数理科学2024年5月号「トポロジカル物質の物理と数理」
第一線の研究者によって書かれた研究の最前線 - 安藤恒也「量子効果と磁場」(1995)
理論・実験両方の研究者によるレビュー - R. E. Prange, S. M. Girvin, "The Quantum Hall Effect 2nd edition" (1989)
量子ホール効果についておそらく初めて書かれた本
分数量子ホール効果の本としては次のようなものがある
- J. K. Jain "Composite Fermions" (2003)
- E. Fradkin "Quantum Field Theory" (2021)
- 永長直人「物性論における場の量子論」(1995)
-
本来ならば電子間にはクーロン斥力が働いている。これが無視できる理由は、自由電子はアルカリ金属などの最外殻原子に相当しており、その背景には正に帯電したイオン核が存在しているため、長距離でも働くクーロン斥力($1/r$)が遮蔽される($e^{-\kappa r}/r$)ため。 ↩
-
Drude理論がDrudeによって提案されたのは1900年であり、当時は電子や原子核は見つかっていなかった。そのため、電子が散乱によって衝突するイオン核については言及されていなかった。 ↩
-
ここで$\rho_{xy}$と$\rho_{yx}$の関係が気になった方は鋭い。この系は等方的であると仮定しているので空間の連続的な回転対称性があるために、$\rho_{yx}=-\rho_{xy}$といった関係がある。 ↩
-
M.A. Paalanen, D.C. Tsui, A.C. Gossard, Phys. Rev. B25 (1982) 5566 ↩
-
K. von Klitzing, G. Dorda, M. Pepper, Phys. Rev. Lett. 45 494 (1980)
ホール抵抗を測定する実験が、なぜ1980年になるまで行われなかったかは、理想的な2次元の自由電子系を準備することの困難と関係している。この測定で使われた理想的な2次元自由電子系は、半導体の接合によって実現された。von Klitzing は1985年にこの業績でノーベル物理学賞を受賞した。実験からわずか5年後の受賞である。 ↩ -
ここでは電子間相互作用は無視できるほど弱いとしている。そのため、1体の電子を考えるだけで十分であり、多体の効果はPauliの排他率のみを通して考慮される。 ↩