先日線形回帰分析に関して、基本的でありながら実務家でも間違った理解をしていることが多い点について解説したんですが、t検定についても、ちょっとおかしいな。と感じることが時々あるので解説と検証を試みました。
とはいえ私も勉強中なので、間違いがあれば指摘いただけるとありがたいです。
ちなみにサンプルサイズ、効果量、検出力についてはいい情報があるので触れていません。本記事ではもっと基本的なトピックを扱います。サンプルサイズ周辺で興味がある方はTJO氏の記事や書籍:サンプルサイズの決め方がおすすめです。特に「サンプルサイズの決め方」はとても良い本だったのでおすすめです。
2023/02/08 追記:Brunner-Munzel検定について間違いがありましたので訂正しました。Brunner-Munzel検定を中央値のようなもので検定すると書いていましたが間違いです。間違いを指摘する記事で自分が間違えるという...。読んでいただいた方申し訳ありません...!
本記事のトピック
- [前編]正規分布の仮定は必要?不必要?
- [後編]Welch?Student?どのt検定を使うのか?
- [後編]t検定の前提が満たされないからBM検定?
- [後編]補足.t検定はあまり使えないのでは...?
2.Welch?Student?どのt検定を使うのか?
前提
2標本のt検定を用いる場合は、仮定によって使い分けがなされますが、私が時々見かけるのは以下のようなパターンですが、これは本当に正しいのでしょうか?
- 対応のあるサンプル:対応のあるt検定
- 対応はなく分散が等しい:Studentのt検定
- 対応はなく分散が等しくない(?):Welchの検定
結論
1標本とみなせるなら対応のあるt検定
他は迷ったらWelch
解説
定義
まずはそれぞれの定義を確認します。
1標本のt検定と対応のあるt検定
$X_1, X_2,,,X_n$を標本データ、$\bar X$を標本平均、$\mu$を母平均とすると
t = \frac{\bar{X} - \mu}{\sqrt{s^2/n}} , \biggl(s^2 = \frac{1}{n-1}\sum_{i=1}^n(X_i - \bar{X})^2\biggr)
は、自由度n-1のt分布になります。
では、対応のあるt検定を用いる場面として、ある学校で新しい教育手法に効果があるかを調査したいとします。5人の生徒を対象に、介入前後でテストの点数が上がったかどうかを検定します。
介入前をX、介入後をYとしてします。
| i=生徒ID | X=前 | Y=後 | D=(Y-X) |
|---|---|---|---|
| 1 | $X_1$ | $Y_1$ | $D_1=Y_1-X_1$ |
| 2 | $X_2$ | $Y_2$ | $D_2=Y_2-X_2$ |
| ・・・ | ・・・ | ・・・ | ・・・ |
| n | $X_n$ | $Y_n$ | $D_n=Y_n-X_n$ |
対応のあるt検定で用いるのはD=(Y-X)の値です。
Dの平均を
\bar{D} = \frac{1}{n}\sum_{i=1}^nD_i
として、Dの標本分散を
s_D^2 = \frac{1}{n-1}\sum_{i=1}^n(D_i - \bar{D})^2
とすると、
t = \frac{\bar{D} - \mu}{\sqrt{s_D^2/n}}
となります。今回帰無仮説を「前後に差がない」とするので、$\mu=0$を代入してt値を求めます。
導出でお分かりのとおり、要するに「対応のある」とは1標本と見なせる場合のことをそう呼んでいる。ということなんですね。
2標本のt検定
ここからは2標本なので、
$X_1, X_2,,,X_m$と$Y_1, Y_2,,,Y_n$を使います。
それぞれの標本平均を $\bar{X}$, $\bar{Y}$, 標本分散を $s_X^2$, $s_Y^2$, とします。
Student
\begin{align}
s^2 &= \frac{(X_1 - \bar{X})^2+\cdots+(X_m - \bar{X})^2+(Y_1 - \bar{Y})^2+\cdots+(Y_n - \bar{Y})^2}{m+n-2}\\
&= \frac{(m-1)s_X^2 + (n-1)s_Y^2}{m+n-2}
\end{align}
として
t = \frac{\bar{X}-\bar{Y}}{\sqrt{s^2\left(\frac{1}{m} + \frac{1}{n}\right)}}
が自由度$m+n-2$のt分布に従います。
Welch
t = \frac{\bar{X}-\bar{Y}}{\sqrt{\frac{s_X^2}{m} + \frac{s_Y^2}{n}}}
v = \frac{\left(\frac{s_X^2}{m} + \frac{s_Y^2}{n}\right)
}{\frac{s_X^4}{m^2(m-1)}+\frac{s_Y^4}{n^2(n-1)}}
の時に、tは近似的に自由度$v$のt分布に従います。
StudentとWelchのt値を比較すると違いがわかりやすいですね。Studentの方はXとYをプールしたものから算出していて、Welchの方は加重平均を使っているようです。自由度についてはだいぶ違いがあるようですね。
さて、実はWelchの検定は本当に「分散が等しくない」と仮定しているのか実験したいと思います。
実験
前回同様、p-valueが一様に分布するか実験します。
今回実験するのは、以下4パターンです。サンプルは全て正規分布から生成します。
| Student | Welch | |
|---|---|---|
| 母分散が等しい2標本 | ||
| 母分散が等しくない2標本 |
まずは平均も分散も等しい正規分布からランダムサンプリングを行い、それぞれのt検定の結果得られるp-valueの分布を比較します。
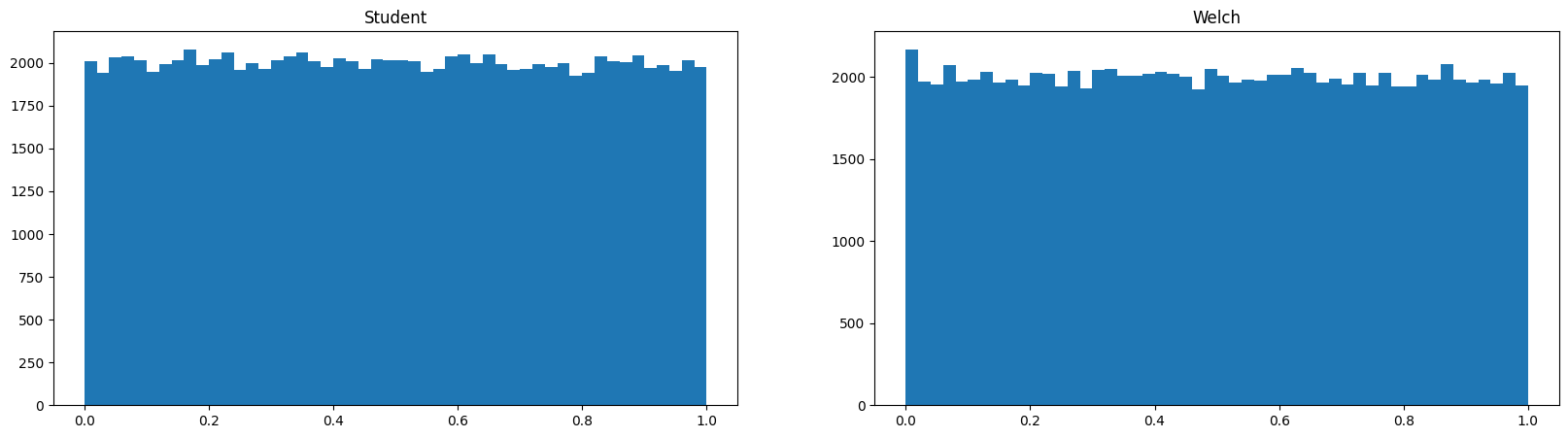
どちらも一様に分布していて、検定にバイアスはかかっていないようです。
次に片方の分散を変えて同じように実験します。
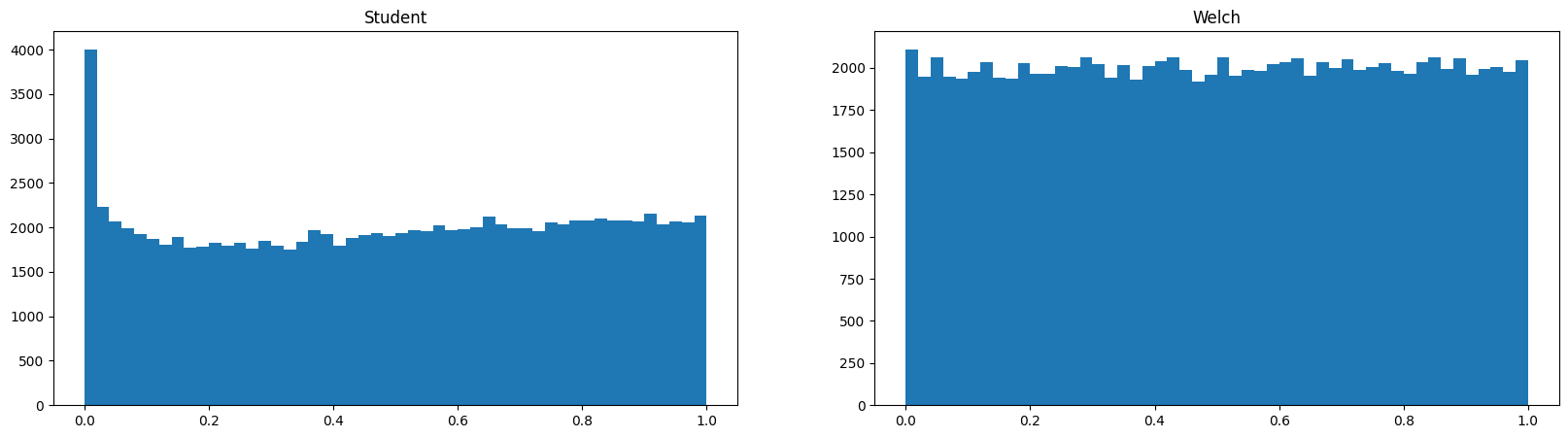
Student(分散が等しいと仮定)は棄却しやすい方にバイアスがかかってしまいました。
ということで、Welchの検定は、「分散が等しくてもそうでなくても」バイアスのない検定ができることがわかりました。
| Student | Welch | |
|---|---|---|
| 母分散が等しい2標本 | バイアスなし | バイアスなし |
| 母分散が等しくない2標本 | バイアスあり | バイアスなし |
ということで実はWelchの検定は等分散か不等分散かで使い分けるものではないようです。
こちら https://biolab.sakura.ne.jp/welch-test-misuse.html や こちら https://oku.edu.mie-u.ac.jp/~okumura/stat/ttest.html でより解説があるのでぜひご一読を。
結論は上記の通りですが、ついでにその他のよくある間違いについて。
分散が等しいかどうかチェックするために、事前にF検定を行うような解説を見かけたのですが、これは間違いです。
多重検定になっていることに加えて、分散が等しくないことは検定で明らかにできますが、等しいことについては明らかにできないからです。この辺りは奥村先生のサイトでも詳しく解説されています。同様に正規性の検定を事前に行うのもNGです。
使用したコード
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats as st
def generateXY(var_equal):
m, n = np.random.randint(low=3, high=100, size=2)
X = st.norm.rvs(size=n)
sd = 1 if var_equal else 2
Y = st.norm.rvs(size=m, scale=sd)
return X, Y
def get_pvalues(var_equal)
welch = []
student = []
for i in range(100000):
X, Y = generateXY(var_equal)
pvalue = st.ttest_ind(X, Y, equal_var=True).pvalue
student.append(pvalue)
pvalue = st.ttest_ind(X, Y, equal_var=False).pvalue
welch.append(pvalue)
return student, welch
3.t検定の前提が満たされないからBM検定?
前提
Brunner-Munzel検定というのは、2標本に対して正規分布の仮定も、等分散の仮定のどちらも必要ない検定です。
t検定の代替手段として解説される場合がありますが、本当に代替できるのでしょうか?
解説
実験
定義については奥村先生のサイトが詳しいです。
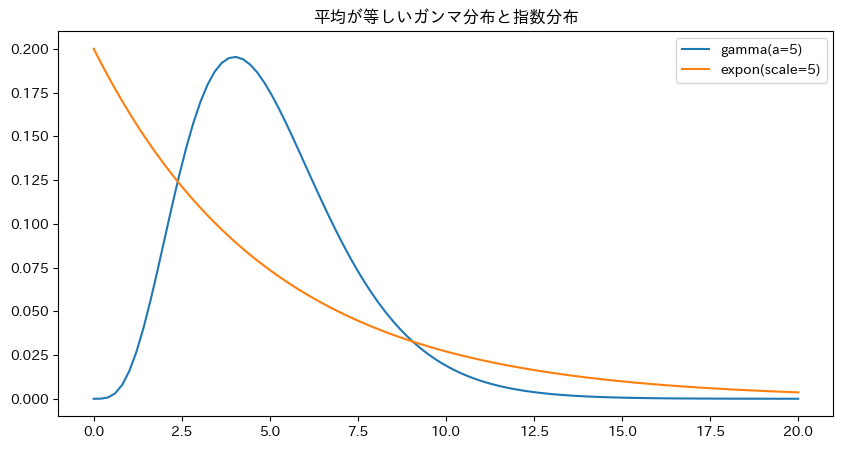
本当に正規分布でなくてもうまくいくのか、ガンマ分布と指数分布のペアで試してみます。
a = 5
gamma = st.gamma(a=a)
lam = gamma.mean()
expon = st.expon(scale=lam)
x = np.linspace(0, 20, 100)
plt.figure(figsize=(10, 5))
plt.plot(x , gamma.pdf(x), label=f'gamma(a={a})')
plt.plot(x , expon.pdf(x), label=f'expon(scale={int(lam)})')
plt.title('平均が等しいガンマ分布と指数分布')
plt.legend();
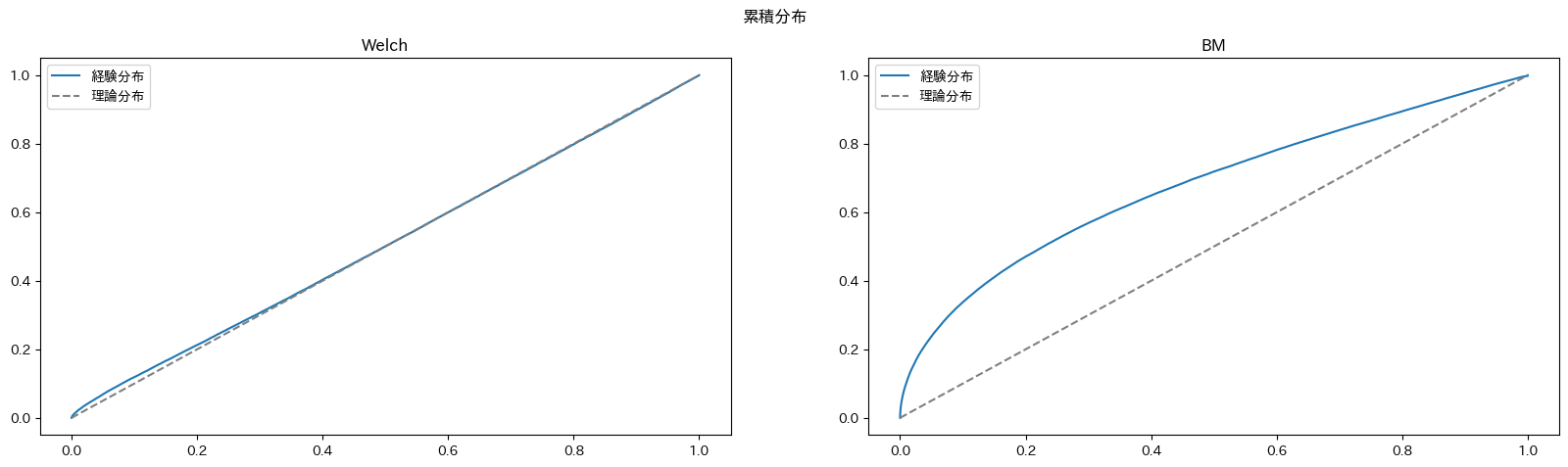
ではこの理論分布をもとにしたサンプルでt検定(Welch), BM検定を比較してみます。
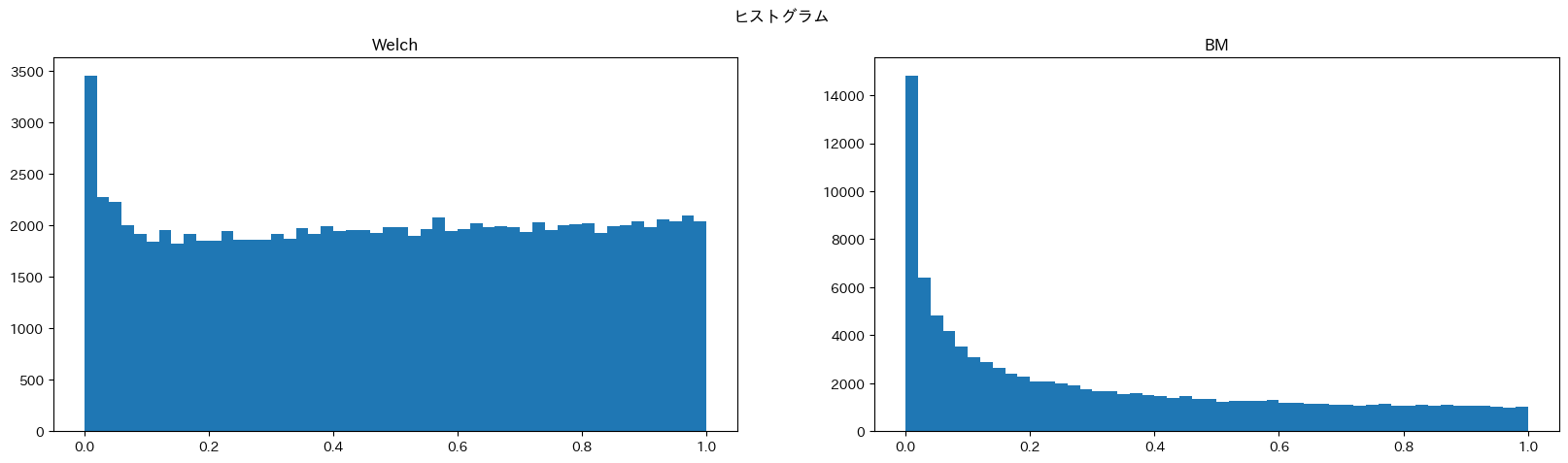
どちらも棄却しやすい方にバイアスがかかっていますが、BM検定の方がより強くバイアスがかかっています。BM検定については私も勉強中でわからないことが多いのですが、t検定の代替として分布を仮定しなくても良いとは言えないことがわかりました。
使用したコード
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats as st
from statsmodels.distributions.empirical_distribution import ECDF
def generateXY(Xdist, Ydist, low, high):
m, n = np.random.randint(low=low, high=high, size=2)
X = Xdist.rvs(size=n)
Y = Ydist.rvs(size=m)
return X, Y
def test(X, Y):
Welch = st.ttest_ind(X, Y).pvalue
BM = st.brunnermunzel(X, Y).pvalue
return Welch, BM
def get_pvalues(Xdist, Ydist, low=3, high=100):
Welchs = []
BMs = []
for i in range(100000):
X, Y = generateXY(Xdist, Ydist, low, high)
Welch, BM = test(X, Y)
Welchs.append(Welch)
BMs.append(BM)
return Welchs, BMs
a = 3
gamma = st.gamma(a=a)
lam = gamma.mean()
expon = st.expon(scale=lam)
Welchs, BMs = get_pvalues(gamma, expon)
plt.figure(figsize=(20, 5))
plt.subplot(1, 2, 1)
plt.hist(Welchs, bins=50)
plt.title('Welch')
plt.subplot(1, 2, 2)
plt.hist(BMs, bins=50)
plt.title('BM')
plt.suptitle("ヒストグラム")
plt.show()
plt.figure(figsize=(20, 5))
plt.plot()
ecdf = ECDF(Welchs)
plt.subplot(1, 2, 1)
plt.plot(ecdf.x, ecdf.y, label='経験分布')
plt.plot([0, 1], [0,1], color='gray', linestyle = "dashed", label='理論分布')
plt.title('Welch')
plt.legend()
ecdf = ECDF(BMs)
plt.subplot(1, 2, 2)
plt.plot(ecdf.x, ecdf.y, label='経験分布')
plt.plot([0, 1], [0,1], color='gray', linestyle = "dashed", label='理論分布')
plt.title('BM')
plt.legend()
plt.suptitle("累積分布")
plt.show()
4.補足 t検定はあまり使えないのでは...?
個人的にはt検定は実は使える場面はとても限定的なのではないかと思っています。
というのも、以下の条件に当てはまらないなら、そもそも検定を用いるメリットがほとんどなくなってしまうんじゃないかなぁと。
1.平均の差がビジネス上意味があるほど大きい
2.誰の目に見ても明らかな差があるとは言えない
1については、例えば施策介入があった場合とそうでない場合の間で、平均値を集計したときに、今後の施策介入コストを考慮するとメリットがない場合、仮説検定を行ったところでその差が大きくなるわけではありません。
2.については、例えばサンプルサイズが小さかったり、サンプルの分散が大きい場合には、ぱっと見で明らかに差があるとは言えないこともあると思います。その場合は仮説検定を実施するメリットはあると思うのですが、誰の目に見ても差があるなら検定しても同じ結果になるだけです。
もちろん、慎重に意思決定をしなければならない場面で、かつ諸々の仮定を満たしているなら有用だとは思うのですが、分析者が所属する組織や扱う課題によっては、全然向かないものもたくさんあるかなと。(まぁそれはどのような手法でも同じか...)
そして何より、帰無仮説とかp-valueとか、非専門家にとっては直感的ではない割に、「統計的に有意」という言葉が「なんか凄そうな感じ」を与えちゃったりするので、私個人としてはできるだけ使いたくないのが本音だったりします。
以上