最近、データサイエンスが流行っていることもあり、線形回帰モデルについても解説記事を見かけることが多くなりました。情報にアクセスしやすくなったのはいいことだと思うんですが、ずっと以前から間違いや解説の不足が多い理論なので、私なりに解説を試みたいと思います。全体的にあまり厳密ではありませんが、線形回帰モデルを学びたての方には有益な記事になるかなと思います。
あと、私も勉強中の身なので、間違いがあったらご指摘いただけたら嬉しいです。
本題
さて、よくある間違いとは以下のような解説です。
- 線形性の仮定が満たされていないので、線形回帰モデルを使ってはいけない
- 残差が正規分布&等分散ではないので、線形回帰モデルを使ってはいけない
- 回帰係数に対するt検定の結果をもとに、p値が大きい説明変数を除外する
- 多重共線性があるとよくないので、変数間で相関が強い、もしくはVIF値が大きい変数を除外する
- AICが小さくなるように変数を選択する
- Lasso回帰で変数を選択する
これらは、線形回帰モデルを「原因と結果の関係を推定」を目的に用いる場合は、どれも間違っているか解説が不足しているかもしれません。
線形性, 残差の正規性, 等分散性
まずは以下についてです。
- 線形性の仮定が満たされていないので、線形回帰モデルを使ってはいけない
- 残差が正規分布&等分散ではないので、線形回帰モデルを使ってはいけない
結論
回帰係数を平均的な因果効果の推定として用いる限り、これらの仮定は絶対に満たさなければならないわけではありません。これらの仮定が満たされない場合に注意するべきは、以下のようなケースです。
- 予測値の区間推定を行う場合、その区間にバイアスがかかる可能性がある。
- 回帰係数の区間推定やt検定を行う場合、その区間やp値にバイアスがかかる可能性がある。
逆に言えば、区間やp値を気にしないのであれば問題ありません。
以下解説です。
最小二乗法と平均
皆さんは平均値をどのように使っていますか?
きっとデータ1件あたりの値の大きさを記述する目的で用いていると思います。
ただし、その目的によっては、代表値として適切でない場合がありますね。
例えば、外れ値があったり、背後の分布が左右対象でなかったりすると、平均値を代表値として用いるとミスリードしてしまう場合があります。
しかし、背後の分布がどうであれ、データ1件あたりの値の大きさを記述する目的ならば解釈は変わらないのもまた事実です。
実はこの平均値の性質を $α+βx$ に拡張したものが線形回帰モデルなんです。
平均値は データの合計 / データの件数 という式で求められますが、この式自体を導出する際に、最小二乗法という、線形回帰モデルの回帰係数を導出するのと同じ方法を用いることができます。
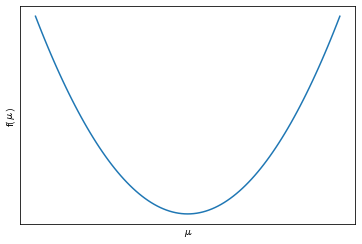
まず以下の分散の公式を使います。 $y_i$ が データで $μ$ が推定したい値とします。
f(μ)=\frac{1}{n}\sum_{i=1}^n(y_i-μ)^2
関数 $f(μ)$ が分散の公式になっています。
$μ$ が決まると値が求まる関数になっており、この $f(μ)$ がなるべく小さくなるように $μ$ を推定することを考えます。この関数は横軸に $μ$ 、縦軸に $f(μ)$ とすると下に「そこ」がある二次関数になります。
$f(μ)$ を微分して $f'(μ)=0$ を $μ$ についてとけば、$f(μ)$ が最小になる $μ$ を求めることができますね。証明は皆さんチャレンジいただくとして、最終的には平均値を求める式を導出できます。
μ=\frac{1}{n}\sum_{i=1}^ny_i
この計算プロセスを線形回帰モデルに当てはめると、 $μ=α+βx$ をこれまでの式に代入するので...
f(α,β)=\frac{1}{n}\sum_{i=1}^n(y_i-(α+βx_i))^2
として、この関数がなるべく小さくなるように α と β を求めます。変数が二つあるので、それぞれ別々に偏微分します。線形回帰モデルは実際にこの方法で回帰係数を推定しています。平均値の導出と全く同じ構造があることがお分かりだと思います。
要するに回帰係数というのは、$x$ 1単位に対して $y$ が平均的に回帰係数分だけ多い、ことをあらわしているだけです。それ以上でも以下でもないので、背後の分布がどんな分布でも非線形な関係があろうとも解釈は変わりません。また、分布が歪んでいる場合、その値を用いる目的によっては代表値として適切でない場合があることも平均値と変わりません。
正規分布の仮定
ただし、推定した y の値に対して正規分布を仮定したい場合は、当然その仮定を満たしている必要があります。
また、回帰係数がt分布に従う、と仮定できるのは前述の正規分布の仮定から来ています。
これはちょうど、データの分布を正規分布と仮定した場合に、母平均の区間推定をt分布で行うのと同じ関係があります。
ただし、t分布の頑健性は回帰係数に対しても同じように働くので、自由度が大きければ実はそれほど影響がなかったりします。
変数選択
結論
以下については「交絡因子と中間因子」を考えるべし。これが結論です。
- 回帰係数に対するt検定の結果をもとに、p値が大きい説明変数を除外する
- 多重共線性があるとよくないので、変数間で相関が強い、もしくはVIF値が大きい変数を除外する
- AICが小さくなるように変数を選択する
- Lasso回帰で変数を選択する
交絡因子
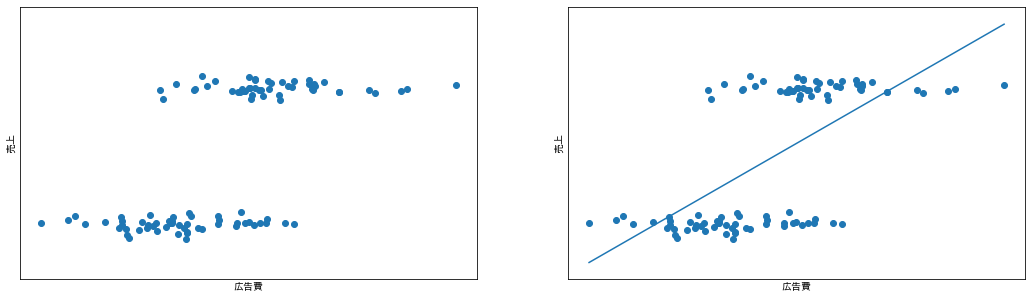
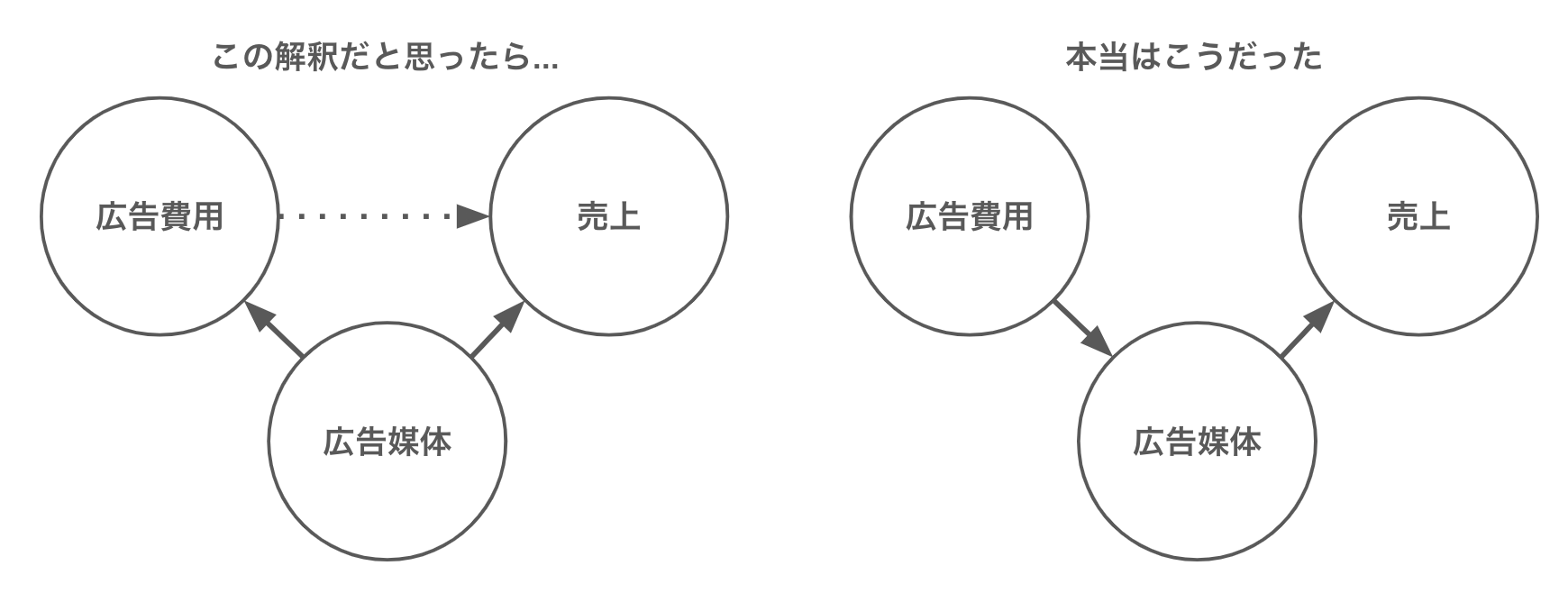
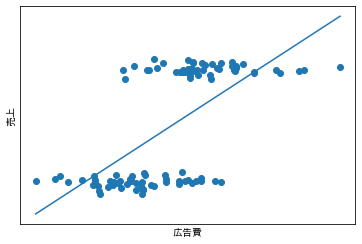
さて、ここからは売上に対する広告費用の効果を推定するシチュエーションを考えてみます。集めてきたデータが以下の図です。左の図に対して、$売上 = α + β × 広告費用$ として線形回帰モデルで推定した結果が右の図です。
線形性の仮定などは前述の説明の通りいったん無視すると、広告費用1単位あたりの平均的な売上効果を推定できそうですね。
ただ、データは2群に分かれていて気持ち悪かったので上司に相談することにしました。
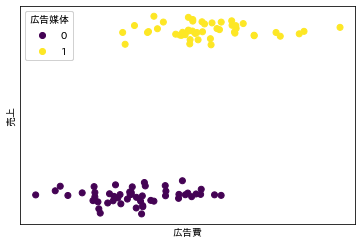
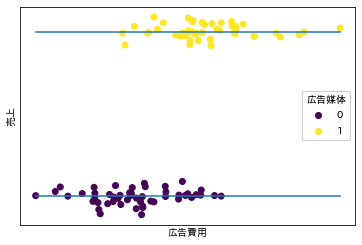
すると、どうやら2群の違いは広告媒体の違いだったようです。
図中で媒体の違いを 0, 1 で表してみます。
見え方がだいぶ変わってきました。
もしかしたら、売上の違いは広告媒体の違いであり、1 の媒体に多く費用がかけられているのは、単に高額な媒体だったからなのかもしれません。
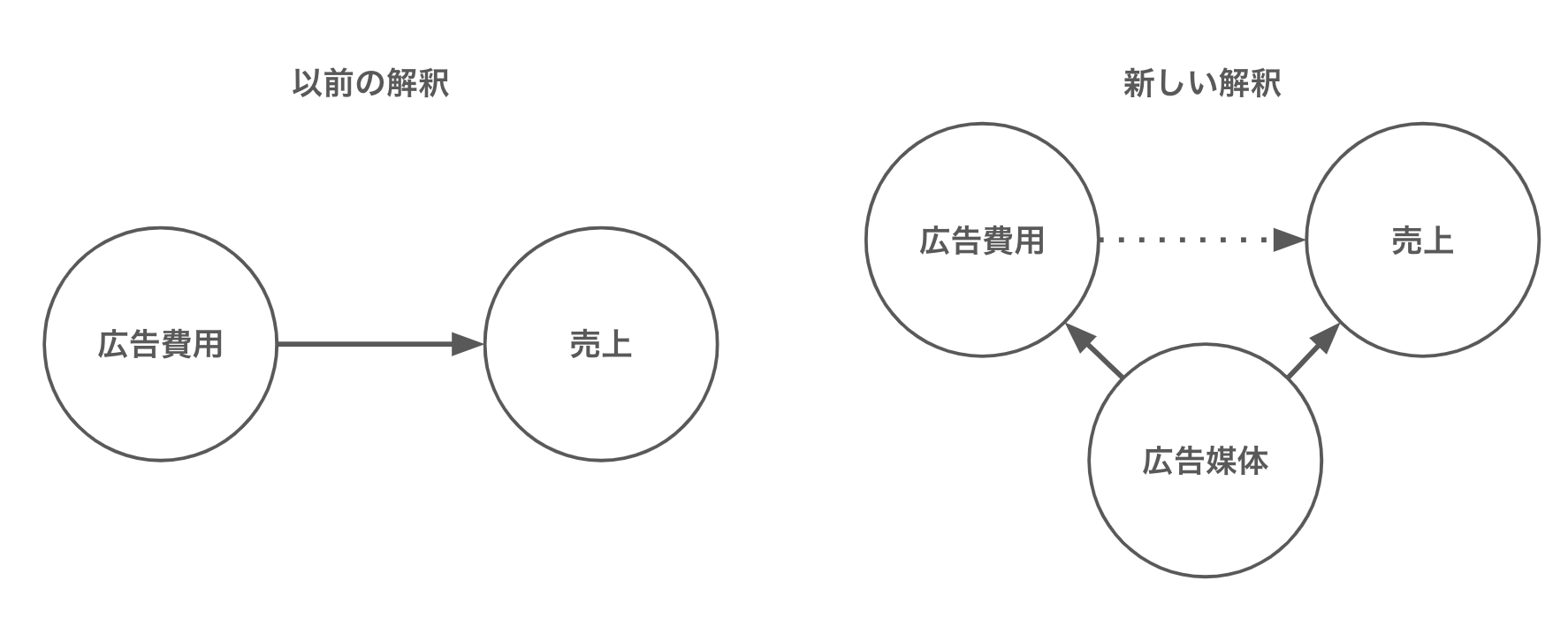
つまり因果関係の解釈が以下のように変化したわけです。
この仮定をモデルに含めるために、広告媒体を 0, 1 の値に変換して線形回帰モデルに組み込むと、以下のように推定されました。
図 回帰式:$売上 = α + β_1 × 広告費用 + β_2 × 広告媒体$
結果は、広告費用に対する回帰係数はほぼゼロになりました。したがって、広告費用は売上には寄与せず、広告媒体だけが売上に寄与している。と解釈できます。今回のような一見すると因果効果があるように見えてしまうような背後の因子を交絡因子と呼び、これが擬似相関の原因になります。
中間因子
広告費用の効果がなさそうだ。と、わかってきたところで、担当者に報告に行きました。すると担当者から「いや、そうじゃなくて、費用をかけるといい媒体に載せてもらえる確率が上がるんですよ!」と言われてしまいました。
どうやら本当の因果関係は以下のような関係だったようです。
この場合は、回帰式に「広告媒体」の変数を含んでしまうと、回帰係数が「広告媒体」に取られてしまうので、「広告媒体」の変数は除外しなければなりません。結局、一番最初のモデルで良かったわけです。
今回のような、原因変数と結果変数の中間に位置して、その因果を媒介する因子を「中間因子」と言います。原因変数から結果変数に対し直接的には影響しませんが、中間因子を通じて影響が伝播する関係になっています。中間因子はモデル式から除外しなければなりません。
変数選択のまとめ
さて、ここまでのストーリーを振り返ってみると、回帰モデルに変数を含めるかどうかは、背後の現象の捉え方に依存していることがわかります。
実はデータだけで因果関係を捉えることは原理的に不可能で、必ず背後のストーリーや仮定、実験計画などが必要になります。したがって、以下のような方法で機械的に指標だけで変数選択を行うのは間違いです。各種指標は背後の現象を考察する上では有益な情報となり得ますが、機械的に決めてはいけません。
- 回帰係数に対するt検定の結果をもとに、p値が大きい説明変数を除外する
- 多重共線性があるとよくないので、変数間で相関が強い、もしくはVIF値が大きい変数を除外する
- AICが小さくなるように変数を選択する
- Lasso回帰で変数を選択する
多重共線性について補足をすると、交絡因子のパターンも中間因子のパターンも、広告費用と広告媒体には強い依存関係があります。しかし、「多重共線性 = 悪いもの」と捉え、考えなしに変数を除外するのは間違いです。交絡因子として必要なのかどうか、背後の関係を考えて慎重に意思決定する必要があります。
最近、機械学習を解釈する技術が発展してきて、例えば shap value を用いた解釈(shap ライブラリの summary_plotとか)などができるようになってきました。これらは機械学習モデルの解釈をする分には良いのですが、因果関係の考察をする場合は、やはり背後のストーリーや仮定、実験計画は不可欠です。
個人的には、どのような手法であれ、背後の現象を私たち人間がどう考えるか、という姿勢は常に重要だと思っています。というか、それがデータ分析の一番楽しいところだと私は感じてます。
以上
データ生成に使ったコード
import numpy as np
from scipy import stats as st
def sigmoid(x):
return 1 / (1 + np.exp(-x))
size = 100 # 生成するデータの件数
x = st.norm.rvs(size=size) # 広告費用
p = sigmoid(2 * x) # 広告費用をかけると媒体が変わる確率がup
z = st.binom.rvs(p=p, n=1) # 媒体の数, ここを変えると媒体の種類を増やせる
e = st.norm.rvs(size=size, scale=0.2) # ノイズ
y = 5 * z + e # 売上
※シードは固定していません。
追記/本当にプロでも間違えているのか?
タイトルを回収するのを忘れてしまいました。以下の論文が詳しいです。
吉田寿夫・村井潤一郎(2021)「心理学的研究における重回帰分析の適用に関わる諸問題」
以上