はじめに
サイバネットの光学ソリューションサイトでは以下のような光学に関する用語を説明しているページがあります。
このようなページ、生成AI全盛の時代に求めている人がいるのかどうか。。
でも、生成AIから出力される説明文や式だけでは理解が進まないと思うんです。
このような技術用語を理解するのに、図も必要です。もっと言うと、実際に感覚的に動かせるミニアプリがあると腹落ちしやすいはず。
なので、今回、単なるテキストと簡単な絵で光学技術用語を紹介するのではなく、インタラクティブに動くJavaScriptアプリとして実装してみようと思います。
今回の光学用語
スネルの法則です。ChatGPTの解説は以下。
スネルの法則(Snell’s law)とは、光が異なる媒質の境界面で屈折するとき、入射角と屈折角の間に成り立つ関係式のことです。光の進む速さが媒質ごとに異なるため、進行方向が変わります。
■ 定義式
n_1 \sin \theta_1 = n_2 \sin \theta_2
■ 各記号の意味
| 記号 | 意味 |
|---|---|
| $$ n_1 $$ | 入射側の媒質の屈折率 |
| $$ n_2 $$ | 出射(屈折)側の媒質の屈折率 |
| $$ \theta_1 $$ | 入射角(境界の法線と入射光線のなす角) |
| $$ \theta_2 $$ | 屈折角(境界の法線と屈折光線のなす角) |
■ 例
空気(屈折率 ≈ 1.0)から水(屈折率 ≈ 1.33)に光が入るとき:
\sin \theta_1 = 1.33 \sin \theta_2
したがって、光は法線側に曲がる(屈折角が小さくなる)。
■ 補足
- 逆に、水から空気へ出る場合($n_1 > n_2$)は光が法線から離れる方向に曲がります。
- $n_1 > n_2$ で、$\theta_1$ がある角度を超えると屈折光が存在しなくなり、全反射が起こります(臨界角以上)。
正しいんですが、、文章が長い!直感的にイメージがしづらい!
では、スネルの法則について楽しく体感できる、JavaScriptアプリを作っちゃいましょう。
使うのはもちろん、ChatGPT。
JavaScriptでスネルの法則が直感的に体験できるウェブアプリ作って
See the Pen Untitled by Hiroyuki Okada (@h-okada_Cybernet) on CodePen.
おー、最初っからかなり良い感じに出来ましたね。
(ChatGPTが、私の過去のチャット履歴を参照した結果かもしれないため、、みなさんの環境でも同様の質のアウトプットが出ない可能性はありますが。。)
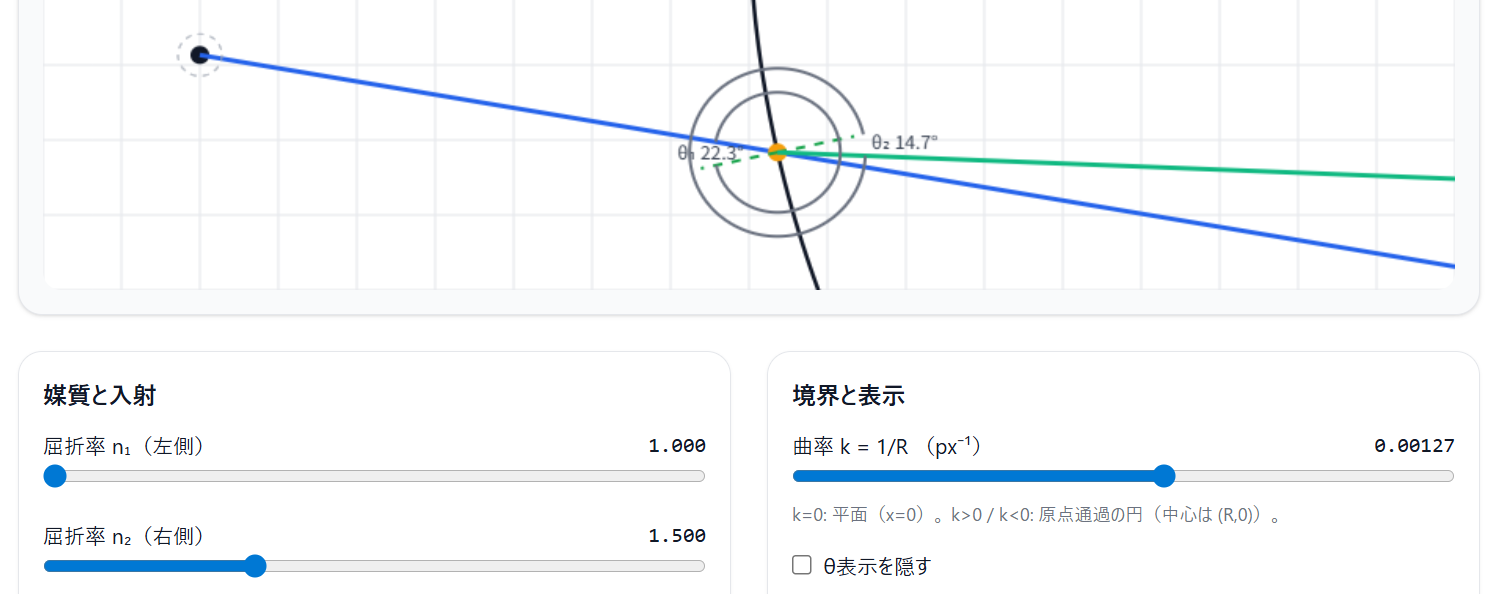
図で光線の屈折の様子が見えて、下のスライドバーで屈折率などのパラメーターを変更できる。
曲率も変えられるし、全反射もちゃんと計算してる。

点線は面法線ですかね。
ちょっと残念なのがθ表示をしたとき。

出射側に入射角度が表示されてますよね。出射角度にいたっては角度範囲から間違ってる。
さて、これを直してもらいましょう。ChatGPT 5.2 Thinkingにお願いしました。
θ表示したとき、入射角と出射角の範囲表記間違ってる。以下のコードを修正して
惜しい!始点と終点は合ってますね。あとは円弧の描画を反転すればOK。
このキャプチャー図を添付して、
円弧の描画を反転して。今円弧ない範囲を描いて、円弧あるところは描かない。入射角も反射角も。
See the Pen Snell2 by Hiroyuki Okada (@h-okada_Cybernet) on CodePen.
おわりに
いかがだったでしょうか?
動かせるミニアプリだったら、直感的に物理計算をイメージできると思います。
次は何を計算するものをつくろうかな♪
※本記事は筆者個人の見解であり、所属組織の公式見解を示すものではありません。
問い合わせ
光学シミュレーションソフトの導入や技術相談、設計解析委託をお考えの方はサイバネットにお問合せください。
