はじめに
みなさんはグラフの計算をするとき何を使ってますか? pajek? それともigraph?
僕は networkxを使ってます。理由はPythonだから。
pajekはwindows専用ソフトだからlinuxで動かないし(wineを使えば動くらしいけど)、igraphはRだから日本語の取り扱いとかパッケージのコンパイル周りのエラーがめんどくさい。
ネットワーク解析そのものを考えるとpajekやigraphの方が伝統があって良さげですが、プログラミング言語そのものの利便性も考えるとトータルでPython+networkxかなと思います。
今回はそんなnetworkxを使って基礎的なグラフの特徴量の計算の仕方を見てみたいと思います。
今回のコードはすべてGistにも上げているのでよかったらそちらもご覧ください。
ネットワーク全体の特徴量
グラフの生成
まず最初に解析対象となるネットワークを生成します。networkxには完全グラフ、ランダムネットワーク、スモールワールドネットワークなど様々なグラフを生成する関数が用意されています。今回はスケールフリーネットワークで試してみます。
import networkx as nx
G = nx.barabasi_albert_graph(30, 1)
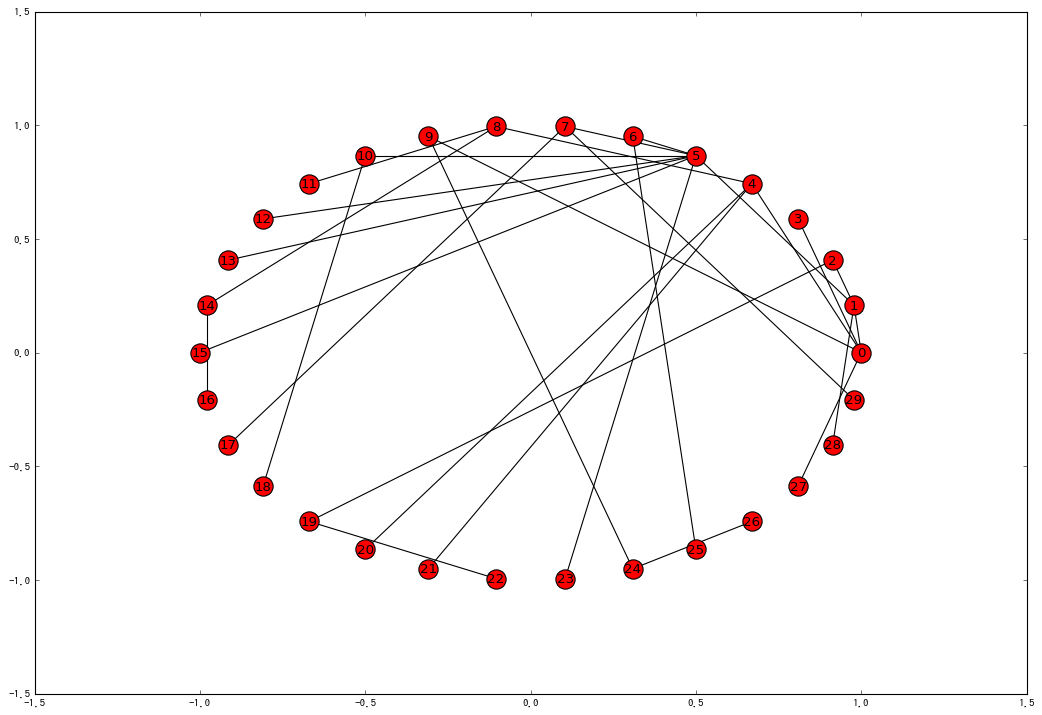
視覚的に確認するには以下のメソッドを使います。
pos = nx.circular_layout(G)
nx.draw_networkx(G, pos)
平均距離
nx.average_shortest_path_length(G)
>> 3.949425287356322
ランダムグラフと比較して
G_random = nx.connected_watts_strogatz_graph(30, 2, 1)
nx.average_shortest_path_length(G_random)
>> 5.917241379310345
スモールワールド性が確認できます。
クラスター係数
nx.average_clustering(G)
>> 0.0
例題のアルバート・バラバシモデルではクラスター係数が小さいという特徴がありますが、今回は0になりました。
中心性
次数中心性
degree_centers = nx.degree_centrality(G)
sorted(degree_centers.items(), key=lambda x: x[1], reverse=True)[:5]
>>>
[(5, 0.27586206896551724),
(0, 0.1724137931034483),
(1, 0.13793103448275862),
(4, 0.13793103448275862),
(7, 0.10344827586206896)]
中心性はそれぞれのノード1つ1つに対して値が辞書形式で与えられます。
これを大きい順に並び替えるには辞書の整列メソッドを使います。
近接中心性
close_centers = nx.closeness_centrality(G)
sorted(close_centers.items(), key=lambda x: x[1], reverse=True)[:5]
>>>
[(1, 0.4027777777777778),
(0, 0.3815789473684211),
(5, 0.3717948717948718),
(4, 0.31521739130434784),
(2, 0.3020833333333333)]
次数中心性と同じ結果になると思っていましたが多少違ってました。他のすべてのノードから平均的に一番近いのは1番のノードみたいです。
媒介中心性
between_centers = nx.betweenness_centrality(G)
sorted(between_centers.items(), key=lambda x: x[1], reverse=True)[:5]
>>>
[(1, 0.6379310344827587),
(5, 0.6108374384236454),
(0, 0.6059113300492611),
(4, 0.3620689655172414),
(8, 0.19704433497536947)]
媒介中心性はあるクラスターとあるクラスターを橋渡しするものが高くなる傾向がありますが、アルバート・バラバシモデルだとそもそもクラスターがないので他の指標とそんなに変わらない結果になってます。
固有ベクトル中心性
eigen_centers = nx.eigenvector_centrality_numpy(G)
sorted(eigen_centers.items(), key=lambda x: x[1], reverse=True)[:5]
>>>
[(5, 0.6148871002455658),
(1, 0.36311628358126075),
(7, 0.2565216963136699),
(0, 0.23924881680129484),
(10, 0.2256761992171005)]
これはハブの近くにあるノードの中心性を押し上げるので、次数中心性の高い5のまわりのノードが軒並みランクインしてます。ちなみにnx.eigenvector_centralityでは収束しなかったのでnumpyバージョンを使っています。