[この記事は制御工学ブログで2024年2月20日に公開されたものを少し修正したものです。]
この記事ではMATLABを用いた制御について画像・動画を交えて説明します。特に、状態フィードバック制御に焦点を当てて説明を行います。MATLABシミュレーションについて説明した動画や関連記事リンクは最下部に置いています。
状態フィードバック制御については以下の記事でまとめています。
状態フィードバック制御の基礎事項
以下のリンクには、状態フィードバック制御の基礎事項を実行するmlxファイルを置いています。その他、MATLABのmファイルおよび実行結果のHTMLファイルを置いています。
MATLABソースへのリンク
メインのファイルは次のものです。
stateeq.m, stateeq.mlx, stateeq.html
実行内容は以下の通りです。
- 可制御性の確認
- 可観測性の確認
- 極配置による状態フィードバック
- 最適レギュレータによる状態フィードバック
MATLABライブスクリプトファイル(mlx)では、極を調整したり、最適レギュレータの重みRを調整したりできます。
実行結果
ここでは、上記ファイルの実行結果について紹介します。制御対象(状態方程式のA,B,C)は以下のように与えるものとします。
A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 0 & 1 \\
-2 & -3 & -1
\end{array}
\right), B=\left(
\begin{array}{c}
0 \\
0 \\
1
\end{array}
\right), C=\left(
\begin{array}{ccc}
2 & 1 & 1
\end{array}
\right)
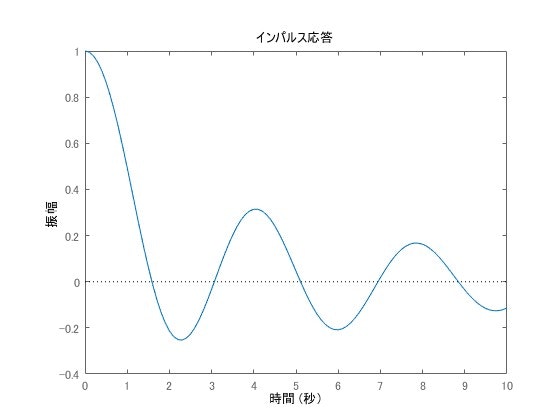
これにインパルス入力を印加した結果がこちらです。
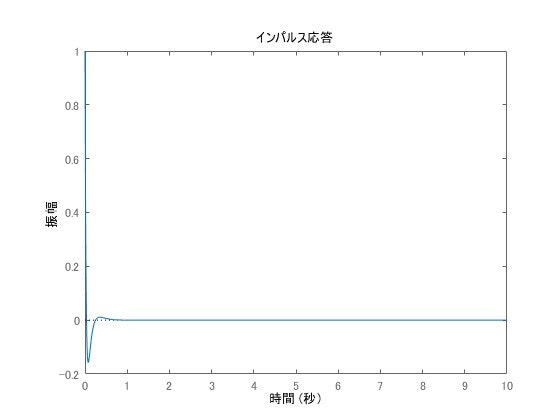
本制御対象は、可制御かつ可観測です。次に、極配置を行った結果を示します。制御対象の次数が3ですので、極は3つ配置し[-10, -12, -20]としました。
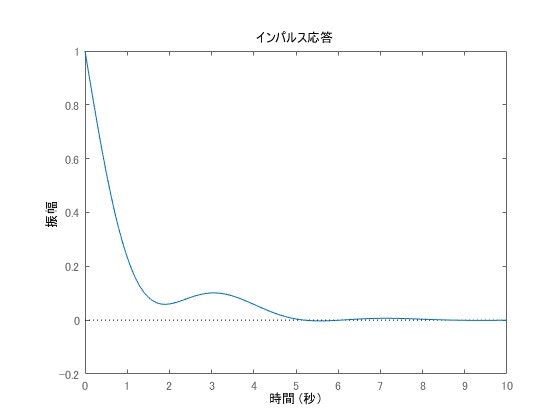
高い速応性を実現できていることがわかります。もちろん、極の配置で応答は変わりますので様々なものを試して頂ければと思います。最後に、最適レギュレータの実行結果を示したいと思います。重み関数はmath Q = 10I(math Iは単位行列)とし、math R=5としました。
リアプノフの安定判別法
以下のリンクから、lyapunov.mlxをダウンロードでき、リアプノフの安定判別法について色々と試行錯誤できます。
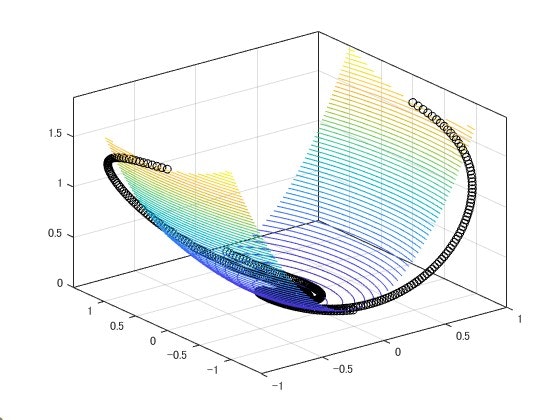
解軌道はあくまで、制御対象に依存して決まります(初期条件にも依存)。しかし、適切にリアプノフ関数を設定することで、システムの安定性を判別することができます。解軌道が等高線から単調に減る方向に動くようリアプノフ関数を設定すると次のようなグラフを作成できます。高さ方向はリアプノフ関数値、平面は状態x1と状態x2です。
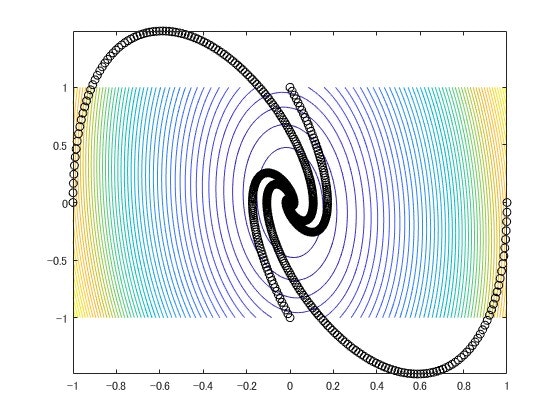
これを2次元に落としたものが次のように表されます。
安定なシステムでリアプノフ関数を探した結果、解軌道が原点に収束する様子が見れると共に、等高線の値が小さくなる方に解軌道が常に進んでいることがわかります。
YouTube: リアプノフの安定判別法(MATLABでの3Dプロット、安定性解析)
クレーンの振れ止め制御
以下のリンクでは、クレーンの振れ止め制御のMATLABファイルを置いています。
MATLABソースへのリンク(アニメーション)
次の動画で、クレーンの振れ止めを状態フィードバックで実現しています。
クレーンの振れ止め制御(最大振れ角が少ない制御を実現するには?
MATLABアニメーションのコードを実行することで、mp4ファイルが作成されます。
MATLAB制御シミュレーションの動画・関連記事
以下はMATLABで制御シミュレーションを実施しているYouTube動画になります。
[MATLAB]極配置と最適レギュレータによる状態フィードバック制御(Live script,現代制御論)
シーソー上ボールの位置決め制御アニメーション(MATLABアニメーション)
関連ページ
制御工学チャンネル(動画ポータルサイト)のMATLABシミュレーションのページです。