HLIBproとは
HLIBproとは
公式のoverviewとかdocumentはここにあります。それを和訳したものを載せておきます。
Oveview
HLIBproは、階層型行列または行列のアルゴリズムを実装するソフトウェアライブラリです。学術目的でバイナリ形式で自由に入手できます。実装はC++でされています。HLIBproは、すべての低レベルアルゴリズムにBLAS / LAPACKを使用するため、対応するソフトウェアライブラリが必要です。
ただまだGPU実装はされていないようです。
さらに、HLIBproには、ACAやHCAのような高密度行列の近似、利用可能な代数の完全集合、幾何学的および代数的クラスタリングなどの様々なクラスタリング技法、ラプラス、ヘルムホルツ、マクスウェル方程式などの積分方程式を離散化するための多くの関数が含まれています。ただし、HLIBproは正方行列しか扱えません。
HLIBproの注目すべき点の一つは、共有(スレッド)および分散メモリ・マシン(MPI)に対するこれらのメソッドの並列化です。これにより、マルチコア・アーキテクチャーまたは高速インターコネクトを備えた並列クラスターを備えた今日のワークステーションでの非常に大きな問題の処理が可能になります。
さらに詳細にいうと、共有メモリアーキテクチャと分散メモリアーキテクチャをサポートしています。
また、HLIBproの注目すべき点のもう一つは、さまざまなアルゴリズムの堅牢性です。これにはフォールトトレラントなアルゴリズムを含み、さらに産業アプリケーションにとって重要な、誤った入力データなどの計算中に発生するエラーハンドリングが含まれます。
既存のデータを簡単に転送するために、Matlab、Harwell-Boeing、MatrixMarket、行列とベクトルのSAMG、PLY、SurfaceMesh、グリッドのGMSHなど、広く使用されている多くのファイル形式がサポートされています。表面関数や行列などの計算データの可視化は、VTK、PostScriptまたはVRMLファイル形式で利用できます。
Manual
Initialisation and Finalisation(初期化とファイナライズ)
HLIBproの関数とクラスにアクセスするには、対応するヘッダファイルをインクルードする必要があります。各ファイルは個別にincludeができますが、generalなヘッダーファイルが用意されています。
# include <iostream>
# include <hlib.hh>
using namespace HLIB;
C言語インタフェース内の関数を除くすべてのHLIBproの関数やクラスは、(参照[HLIBpro_C] )、HLIB名前空間内に入っています。これらの関数の呼び出しを簡単にするために、usingコマンドによって現在の名前空間に表示されます。
Matrix Construction(マトリックス構築)
𝖧𝖫𝖨𝖡𝗉𝗋𝗈中のマトリックス構造が与えられたブロックのクラスタツリーを使用してのプロセッサである$ T $と内のすべての葉のための行列を構築$ T $し、すべての内部ノードのため$ T $。リーフマトリックスは、マトリックスの実際の内容を定義し、例えば密(TDenseMatrix)および低ランク(TRkMatrix)マトリックスのような様々なフォーマットであり得る。一方、内側のノードはℋ行列の階層を定義し、行列代数にとって重要です。このようなブロック行列は、通常型TBlockMatrixのです。
ブロック行列の特別なバージョンはTHMatrixであり、行列ベクトル乗算中の未知数の内外の順序付けをマップするためにブロッククラスタツリーによって供給される順列も格納されます。例えばTBlockMatrix型の標準ブロック行列は、未知数の順序を知るだけである。
編集途中(調べてる途中でMAGMA使おうってなったので、一旦打切り)
 MAGMA
MAGMA
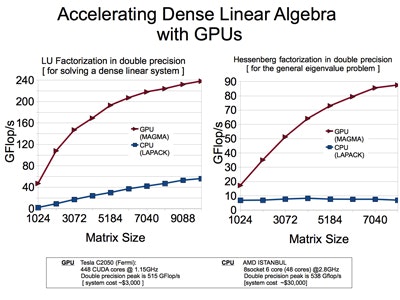
Dongarra's GroupによるGPUおよびマルチコアCPU上のLAPACK
 そもそもLAPACKとは
そもそもLAPACKとは
BLAS, LAPACKとは何か:世界最高の線形代数演算パッケージ
コンピュータで線形代数演算を行うライブラリはBLAS[1]およびLAPACK[2]が、間違いなく世界最高のものである。無料で入手でき、品質、信頼性が高く、網羅している演算の種類も多く、サードパーティによる高速な実装もあるからだ。プログラムは一度は自分で書いた方がいいが、このクオリティは並大抵のものではないので、中身を勉強しつつこのライブラリに頼ることは良いことである。ただ、BLAS, LAPACKは密行列向けであり、疎行列はサポートされていない点に注意。
LAPACKとは?
LAPACK(Linear Algebra PACKage)もその名の通り、線形代数パッケージである。BLASをビルディングブロックとして使いつつ、より高度な問題である連立一次方程式、最小二乗法、固有値問題、特異値問題を解くことができる。また、それに伴った行列の分解(LU分解、コレスキー分解、QR分解、特異値分解、Schur分解、一般化Schur分解)、さらには条件数の推定ルーチン、逆行列計算など、様々な下請けルーチン群も提供する。品質保証も非常に精密かつ系統的で、信頼のおけるルーチン群である。また、BLASとは違い、バージョン3.2からはFortran 90で書かれ、2011/2/15現在バージョン3.3.0が出ている。特に今回は標準的なCのAPI, CS分解、Level 3 BLASを多用したソルバ、完全なスレッドセーフの実現、がハイライトとされている。3.3.0は、1632ものルーチンからなっている。単精度、倍精度、複素数単精度、複素数倍精度について各400個程度のルーチンがある。パソコンからスーパーコンピュータまで、様々なCPU, OS上で動き、webサイトはなんと9000万ヒットである。世界中の人に愛されている素晴らしいライブラリである。
GPU向けBLAS, LAPACK:近年CPUの性能が頭打ちになっている一方、グラフィックスボードの高性能化が著しくそれを計算に使うことも行われている。CPUに比べ、数倍~10倍程度高速かつ安価なので、大変注目されている。nVidia社のGPUを用いたMAGMAプロジェクトが有望だと考えている。
- http://www.jsces.org/Issue/Journal/pdf/nakata-0411.pdf
- http://www.netlib.org/utk/people/JackDongarra/WEB-PAGES/SPRING-2014/lect10-2.pdf
Oveview
の翻訳をすると、
GPUとマルチコアアーキテクチャ上の行列代数
MAGMAプロジェクトは、LAPACKに類似した高密度線形代数ライブラリを開発することを目指していますが、現在の「Multicore + GPU」システムから始まるヘテロジニアスハイブリッドアーキテクチャ向けです。
MAGMAの研究は、新興ハイブリッド環境の複雑な課題に対処するために、最適なソフトウェアソリューション自体がハイブリッド化し、単一のフレームワーク内で異なるアルゴリズムの強みを組み合わせなければならないという考えに基づいています。このアイデアを基に、ハイブリッド・マルチコアとGPUシステムのための線形代数アルゴリズムとフレームワークを設計し、各ハイブリッド・コンポーネントが提供するpowerをアプリケーションが完全に活用できるようにします。
も翻訳すると
インテル、AMD、IBM、NVIDIAなどの大手チップメーカの最近の活動は、マイクロプロセッサと大型HPCシステムの将来の設計が本質的に混成/異種であることをより明白にしています。
以下はコンポーネントの2つの主要なタイプ:
1)パワーウォール、命令レベルの並列性の壁、およびメモリの壁を避けながら、チップ上にますます多くのコンポーネントをパックしたいという要望のため、コアの数が増え続ける、多くのコアのCPUテクノロジがあリます。
2)汎用製品に搭載されている特殊目的のハードウェアとアクセラレータ、特にグラフィックスプロセッシングユニット(GPU)は、近年浮動小数点性能の標準CPUを上回り、マルチコアCPUよりもプログラミングが簡単ではないにしても簡単になりました。
将来の設計におけるこれらのコンポーネントタイプの相対的なバランスは明確ではなく、時間の経過とともに変化する可能性があるが、ラップトップからスーパーコンピュータまでの将来の世代のコンピュータシステムは、異機種コンポーネントとなるでしょう。
みたいなことが書いてあります。
Feature
- 優れた性能と高精度(LAPACKに準拠)
- 複数精度演算サポート(S / D / C / Z)
- マルチコアCPUとGPUの両方を使用したハイブリッドアルゴリズム
Document
を翻訳してみます。
MAGMA Users' Guide
MAGMAプロジェクトの目標は、現在のマルチコア+マルチGPUシステムから始めて、異種アーキテクチャでの正確なソリューションを可能な限り早く実現する新しい世代の線形代数ライブラリを作成することです。これらのシステムの異質性、大規模な並列性、および計算速度とCPU-GPU通信速度のギャップに起因する複雑な課題に対処するため、MAGMAの研究は、最適なソフトウェアソリューション自体がハイブリッド化し、アルゴリズムを単一のフレームワーク内で使用できます。このアイデアを基にして、ハイブリッドマルチコアとマルチGPUシステムのための線形代数アルゴリズムとフレームワークを設計し、各ハイブリッドコンポーネントが提供するpowerをアプリケーションが完全に活用できるようにします。
MAGMAライブラリは、関数、データストレージ、インタフェースでLAPACKに似ているように設計されており、既存のソフトウェアコンポーネントをLAPACKからMAGMAに簡単に移植し、新しいハイブリッドアーキテクチャを利用することができます。 MAGMAユーザーは、ライブラリを使用するためにCUDAを知る必要はありません。
LAPACKスタイルのインターフェイスには2種類あります。最初のものは、CPUインタフェースと呼ばれ、入力を受け取り、その結果をCPUのメモリに生成します。第2は、GPUインタフェースと呼ばれ、入力を受け取り、結果をGPUのメモリに生成します。どちらの場合も、ハイブリッドCPU / GPUアルゴリズムが使用されます。また、CUBLASルーチンを補完するMAGMA BLASも含まれています。
Installing MAGMA
まず、サンプルの1つをテンプレートとして使用してmake.incファイルを作成します。
.cshrc / .bashrcファイルまたはmake.incファイル自体に、外部パッケージがインストールされている場所の環境変数を設定します。たとえば、CUDAとIntel MKLのインストール先を指定するには、cshを使用します。
setenv CUDADIR /usr/local/cuda
# sourcing this script sets MKLROOT
source /opt/intel/composer/bin/compilervars.csh intel64
sh/bashを使って:
CUDADIR=/usr/local/cuda
source /opt/intel/composer/bin/compilervars.sh intel64
Fortranコンパイラがない場合は、FORTをコメントアウトしてください。MAGMAのFortran 90インターフェースとFortranテスターはビルドされません。また、多くのテスターは結果を確認することができません。例えば以下のようなエラーメッセージを出力します。
magma/testing> ./testing_dgehrd -N 100 -c
...
Cannot check results: dhst01_ unavailable, since there was no Fortran compiler.
100 --- ( --- ) 0.70 ( 0.00) 0.00e+00 0.00e+00 ok
共有ライブラリをコンパイルするには、最初にmake.incのCFLAGS、FFLAGSなどに-fPICを追加します。make.inc.mkl-sharedの例を参照してください。
make shared
make test
make install prefix=/usr/local/magma
静的ライブラリをコンパイルするには:
make lib
make test
make install prefix=/usr/local/magma
これにより、$(prefix)/libにlibmagma.aとlibmagma.so(コンパイルされている場合)、$(prefix)/includeにMAGMAヘッダーファイルがインストールされます。$(prefix)/lib/pkgconfig/magma.pc for pkg-config.でもインストールされます。
Running tests
テストディレクトリには、ほとんどのMAGMA機能のテストが含まれています。
これらは例として役立ちますが、アプリケーションに必要としない、または異なる動作をする追加のテスト機能が含まれています。 サンプルディレクトリには、この追加のフレームワークがまったくない単純な例があります。
テストサイズとオプションの標準セットを実行するには、testing/run_tests.pyファイルを参照してください。 ほとんどのテストは-tol100で合格します。デフォルトの許容差、通常は30で、いくつかのテストでは偽陰性が示されます。ここでのテストは大丈夫ですが、精度許容差チェックのわずかに上です。
Example
exampleディレクトリには、単純なスタンドアロンの例が示されています。
これは、MAGMA Makefilesとテスト用に開発した他の特別なフレームワークとは別に、MAGMAを使用する方法を示しています。
Overview
MAGMAのインターフェースは、既存のコードの移植を容易にするためにLAPACKに似ています。
多くのルーチンは、LAPACKと同じ基本名と同じ引数を持ちます。場合によっては、効率的なアルゴリズムを実装するために、MAGMAはより大きなワークスペースや追加の引数を必要とします。
MAGMAのルーチンのいくつかのクラスがあります。
- ドライバルーチン -全体の問題を解決します。
- 計算ルーチン -問題の1枚を解決します。
- BLASルーチン -基本線形代数サブルーチン。これらは線形代数アルゴリズムの基礎を形成します。
- 補助ルーチン -追加BLASのようなルーチン、多くはもともとLAPACKで定義されました。
- ユーティリティ・ルーチン -追加ルーチン、GPUプログラミングに多くの特定。
ルーチンの簡単な概要をここに示しました。個々のルーチンの詳細な説明は、モジュールのセクションにあります。
ドライバー&計算ルーチンはmagma_という接頭辞を持ちます。これらは一般的にハイブリッドCPU / GPUアルゴリズムです。接尾辞は、計算が実行される場所ではなく、行列がどのメモリ内で開始および終了するかを示します。
| suffix | Example | 説明 |
|---|---|---|
| none | magma_dgetrf | ハイブリッドCPU / GPUルーチンであり、マトリックスは当初CPUホストメモリ内にある。 |
| _m | magma_dgetrf_m | ハイブリッドCPU /マルチGPUルーチンで、マトリックスは当初CPUホストメモリにあります。 |
| _gpu | magma_dgetrf_gpu | ハイブリッドCPU / GPUルーチンであり、マトリックスは当初GPUデバイスメモリ内にある。 |
| _mgpu | magma_dgetrf_mgpu | ハイブリッドCPU /複数GPUルーチンであり、マトリクスは複数のGPUのデバイスメモリに分散されています。 |
一般に、MAGMAはLAPACKの命名規則に従います。各ルーチンのベース名は、1文字の精度(時には2文字)、2文字の行列タイプ、および通常は2〜3文字のルーチン名を持ちます。たとえば、DGETRFはD(倍精度)、GE(一般行列)、TRF(三角因子分解)です。
| Precision | 説明 |
|---|---|
| s | 単精度実数(浮動小数点数) |
| d | 倍精度実数(倍精度) |
| c | 単一複素数精度(magmaFloatComplex) |
| z | 二重複素数精度(magmaDoubleComplex)) |
| sc | 単精度結果を持つ単一複素数入力(たとえば、scnrm2) |
| dz | 倍精度結果を持つdouble-complex入力(例:dznrm2) |
| DS | 混合精度アルゴリズム(doubleとsingle、例えば、dsgesv) |
| ZC | 混合精度アルゴリズム(double-complexとsingle-complex、例えば、zcgesv) |
| Matrixtype | 説明 |
|---|---|
| ge | 一般行列 |
| sy | 対称行列、実数または複素数) |
| he | エルミート(複素)行列 |
| po | 正定値、対称(実数)またはエルミート(複素)行列 |
| tr | 三角行列 |
| or | 直交(実数)行列 |
| un | 単一(複素)マトリックス |
Driver routines
ドライバルーチンは問題全体を解決します。
| Name | 説明 |
|---|---|
| gesv | 線形システムを解く、$AX = B、A$はgeneral(非対称) |
| posv | 線形システムを解く、$AX = B、A$は対称/エルミート正定値 |
| hesv | 線形システムを解く、$AX = B、A$は対称不定 |
| gels | 最小自乗解法、$AX = B、A$は長方形 |
| geev | 非対称固有値ソルバー、$AX = X Lambda$ |
| syev/heev | 対称固有値ソルバー、$AX = X Lambda$ |
| syevd/heevd | 対称固有値ソルバー、$AX = X Lambda$、分割統治を使用 |
| sygvd/hegvd | 対称一般化固有値ソルバー、$AX = BX Lambda$ |
| gesvd | 特異値分解(SVD)、$A = U \Sigma V ^ H$ |
| gesdd | 分割統治を使用した特異値分解(SVD)、$A = U \Sigma V ^ H$ |
divide and conquer algorith(分割統治法)に関しては以下を参考に
Computational routines
計算ルーチンは問題の1つを解決します。通常、ドライバルーチンは、問題全体を解決するためにいくつかの計算ルーチンを呼び出します。ここで、中括弧{}は類似のルーチンをグループ化します。スター付き*ルーチンはまだMAGMAに実装されていません。
1. 三角因子分解に関して
| Name | 説明 |
|---|---|
| getrf、potrf、hetrf | 三角因子分解(LU、Cholesky、Indefinite) |
| getrs、potrs、hetrs | 三角形の前方および後方の解決 |
| getri、potri | 三角逆関数 |
| getf2、potf2 | 三角形パネル分解(BLAS-2) |
2. 直交分解 に関して
| Name | 説明 |
|---|---|
| GE { QRF、QLF、LQF、RQF *} | QR、QL、LQ、RQ分解 |
| geqp3 | 列ピボットを伴うQR(BLAS-3) |
| or{ MQR、MQL、MLQ、MRQ*} | 因数分解後のQ倍(実数) |
| un{ MQR、MQL、MLQ、MRQ*} | 因数分解(複素数)後にQを掛ける |
| or{ GQR、GQL 、glq、GRQ*} | 因数分解後のQを生成する(実数) |
| un{ GQR、GQL 、glq、GRQ*} | 因数分解後のQを生成する(複素数) |
3. 固有値とSVDに関して
| Name | 説明 |
|---|---|
| Gehrd | ヘッセンベルク削減(in geev) |
| sytrd / hetrd | 三重対角化(syev、heev) |
| gebrd | 二重対角縮小(gesvd) |
MAGMAとLAPACKの内部にある多くの計算ルーチンがあり、一般的にエンドユーザからは呼び出されません。
BLAS routines
BLASルーチンは、精度、行列タイプ(レベル2と3)、ルーチン名のような命名規則に従います。BLASルーチンの場合は、magma_プレフィックスは一方で、(cublasZgemmを呼び出しmagma_zgemm例えば、)CUBLASのラッパーを示しmagmablas_プレフィックスは私たち自身のMAGMAの実装(例えば、magmablas_zgemm)を示しています。すべてのMAGMA BLASルーチンはGPUネイティブで、GPUメモリのマトリックスを取ります。ここでの説明は簡略化され、スカラー(アルファ&ベータ)と転置が省略されています。
BLAS-1:ベクトル演算
これらはO(n)データに対してO(n)演算を行い、メモリにバインドされます。
BLAS-2:行列 - ベクトル演算
これらはO(n ^ 2)データに対してO(n ^ 2)回の演算を行い、メモリにバインドされます。
BLAS-3:行列 - 行列演算
これらはO(n ^ 2)データに対してO(n ^ 3)演算を行い、演算にバインドされます。レベル3のBLASは、メモリ結合レベル1およびレベル2のBLASよりもかなり効率的です。
Auxiliary routines
追加BLASのようなルーチン、多くはもともとLAPACKで定義されています。これらは同様の命名規則に従います:精度、次に "la"、次にルーチン名。MAGMAはこれらの一般的なものをGPU上に実装し、対称や転置などのいくつかを追加します。
補助ルーチンの場合、magmablas_プレフィックスは、私たち自身のMAGMAの実装(例えば、magmablas_zlaswp)を示しています。すべてのMAGMA補助ルーチンはGPUネイティブであり、GPUメモリのマトリックスを取ります。
Utility routines
メモリの割り当て
MAGMAは、mallocまたはnewで割り当てられた通常のCPUメモリを使用できますが、整列された、特に固定されたメモリを使用すると、より良いパフォーマンスが得られます。sizeofをキャストして使用する必要性を避けるこれらの型付きバージョン(例えばmagma_zmalloc)と、より柔軟であるが(void **)キャストを必要とする型指定されていないバージョン(例えばmagma_malloc)サイズによって。
*は4つの精度のうちの1つです(sdcz、またはmagma_int_tの場合はi、un-typedの場合はnone)。
コミュニケーション
通信ルーチンの名前は、CPUの観点からのものです。
| Name | 説明 |
|---|---|
| setmatrix | GPUに行列を送る |
| setvector | ベクトルをGPUに送る |
| getmatrix | GPUから行列を得る |
| getvector | GPUからベクトルを得る |
Data types & complex numbers
整数
MAGMAはmagma_int_tを整数に対して使います。通常、これはC/C++ int型にマップされます。今日のシステムでは、LP64の規約を使用しています。つまりlongとポインタは64ビットですが、intは32ビットです。
MAGMAはまた、int、long、およびポインタがすべて64ビットのILP64規約を代替としてサポートしています。これを使用するには、magma_int_tをlong型にtypedefします。ILP64を使用するには、コンパイル時にMAGMA_ILP64またはMKL_ILP64を定義し、ILP64 BLASおよびLAPACKライブラリとリンクします。make.inc.mkl-ilp64の例を参照してください。
複素数
MAGMAは複素数をサポートしています。残念ながら、C/C++で複素数を実装する方法の基準は1つではありません。幸運なことに、ほとんどの実装はバイナリレベルで同一なので、自由にキャストすることができます。MAGMAの種類は次のとおりです。magmaFloatComplexの場合はCUDA MAGMAでcuFloatComplexにtypedefしましょう、magmaDoubleComplexの場合はCUDA MAGMAにてcuDoubleComplexにtypedefしてください。
Cでは、複素数を操作するマクロを提供しています。C++サポートの場合は、magma_operators.hヘッダーをインクルードします。このヘッダーは、オーバーロードされたC++演算子と関数を提供します。
Conventions for variables (変数の表記法)
変数名の一般的なガイドラインは次のとおりです。もちろん、これらの例外はあります。
大文字はA、B、C、Xの行列を示します。
小文字はベクトルを示します:b、x、y、z
"d"接頭辞は、GPUデバイス上の行列またはベクトルを示します。dA、dB、dC、dX; db、dx、dy、dz。
ギリシャ語はスカラーを表します:alpha, beta
m、n、kは行列の次元です。
通常、引数の順序は次のとおりです。
オプション(uploなど)
行列サイズ(m、n、kなど)、
入力行列とベクトル(A、lda、x、incxなど)
出力行列とベクトル
workspaces (work, lwork, etc.)
エラーコードの情報
LAPACKとMAGMAは列主行列(column-major matrices)を使用します。次元(lda、n)を有する行列$X$について、要素$X(i、j)$はX[i + j * lda]である。対称、エルミート、および三角行列の場合、uplo引数で指定すると、下三角または上三角だけがアクセスされます。他の三角形は無視されます。
ldaは行列$A$の先行次元(leading dimension)です。同様に、$B$はldb、$dA$はddaなどである。それらは引数リストの行列ポインタの直後にあるべきである。先頭の次元は行数であってもよく、またはAがより大きい親行列の部分行列である場合、ldaは親行列の先行する次元で例えば、行などです。
GPUでは、優れたパフォーマンスを提供するために、先頭のディメンションを32の倍数に丸めるのが有益な場合があります。これにより、メモリ読取りが合体するように調整されます。これはmagma_roundup関数によって提供されます
ldda = magma_roundup( m, 32 );
数式((m + 31)/32)*32も機能しますが、floored整数除算に依存しますが、検索関数はより明確になります。
CPUでは、TLBミスを最小限に抑えるために、リーディングディメンションがページサイズの倍数(多くの場合4KiB)でないことを保証することは、しばしば有益です。
ベクトルの場合、incxはベクトルxの要素間の増分またはストライドです。 ほとんどの場合、incx <0の場合、ベクトルは逆順で、たとえばMatlab表記を使用して索引付けされ、
incx = 1 means x( 1 : 1 : n )
incx = 2 means x( 1 : 2 : 2*n-1 )
もしくは
incx = -1 means x( n : -1 : 1 )
incx = -2 means x( 2*n-1 : -2 : 1 )
いくつかのルーチン(amax、amin、asum、nrm2、scal)では、順序は関係がないので、負のincxは許されません。 incx> 0である。
Constants
MAGMAは、CBLASおよびLAPACKパラメータに相当する、MagmaTrans、MagmaNoTransなどのいくつかの定数パラメータを定義します。 これらのパラメータの命名と番号付けは、NetlibのCBLAS、NetlibのLAPACKへのCインタフェース、およびPLASMAに従います。
MAGMAには、MAGMAの整数定数を受け取り、LAPACKの文字列定数を返す関数lapack_xyz_const()が含まれています。ここで、xyzはuplo、transなどのMAGMA型です。LAPACKの観点からは、各文字列の最初の文字だけが重要です。 それにもかかわらず、この関数は、 "Transpose"、 "Transpose"、 "Upper"、 "Lower"などの意味のある文字列を返します。同様に、MAGMAの整数定数からCBLAS、OpenCLのclBLAS、およびCUDAのcuBLAS整数 定数。
magma_xyz_const()関数は、LAPACKの文字列定数からMAGMAの整数定数に逆方向に移動する関数もあります。
最も一般的な定数は、BLASルーチン用に定義された定数です。
- enum{MagmaNoTrans、MagmaTrans、MagmaConjTrans} magma_order_t
行列が転置、転置、コンジュゲート転置されないかどうか。 実行列の場合、TransとConjTransは同じ意味を持ちます。
- enum {MagmaLower、MagmaUpper、MagmaFull} magma_uplo_t
行列の下三角形または上三角形を指定するか、または完全な行列にするか。
- enum {MagmaLeft、MagmaRight} magma_side_t
行列が左か右のどちらにあるか。
- enum{MagmaUnit、MagmaNonUnit} magma_diag_t
対角を単位(すべて1)とするかどうか。
特定のルーチンの追加の定数は、ルーチンのドキュメントで定義されています。
MAGMA、CBLAS、LAPACK、CUBLAS、およびclBlasは潜在的に異なる定数を使用するため、それらの間のコンバータが提供されます。
これらはLAPACK定数をMAGMA定数に変換します。 LAPACK定数の意味はコンテキストに依存することに注意してください。 'N'はFalse、NoTrans、NonUnit、NoVecなどを意味します。
Errors
ドライバと計算ルーチン、BLAS/補助ルーチンは現在、戻り値とinfo引数の両方でエラーを返します。 戻り値と情報は常に同じでなければなりません。 一般的には、この表の意味があります。 あらかじめ定義されたエラーコードは大きな負数です。 下記の記号定数を使用することをお勧めしますが、数値はinclude/magma_types.hにあります。
| info | 説明 |
|---|---|
| info = 0 (MAGMA_SUCCESS) | 成功して終了 |
| info < 0, but small | info = -iの場合、i番目の引数の値が不正です |
| info > 0 | 特異行列などの関数固有のエラー |
| MAGMA_ERR_DEVICE_ALLOC | GPUデバイスメモリを割り当てることができませんでした |
| MAGMA_ERR_HOST_ALLOC | CPUホストメモリを割り当てることができませんでした |
| MAGMA_ERR_ILLEGAL_VALUE | 引数には不正な値がありました(代わりに、i番目の引数が悪いと言って-iを返す必要があります) |
| MAGMA_ERR_INVALID_PTR | ポインタをfreeできません |
| MAGMA_ERR_NOT_IMPLEMENTED | 機能またはオプションが実装されていない |
| MAGMA_ERR_NOT_SUPPORTED | 現在のアーキテクチャでサポートされていない機能またはオプション |
magma_xerbla()はエラー(主に不正な引数)をユーザに報告するために呼び出されます。
magma_strerror()は、エラーコードの文字列の説明を返します。
Methodology
One-sided matrix factorizations
片側LU、コレスキー、およびQR分解は、線形システムを解決するための基礎を形成します。一般的なn行n列の行列にはLU、対称/エルミート正定値(SPD)行列にはコレスキー、最小二乗問題はQRで、
min || Ax-b ||
一般的なm×n、m> n行列の場合
計算がGPUとCPUの間で分割されているハイブリッドアルゴリズムを使用します。一般に、片面分解の場合、パネルはGPU上のCPUおよび末尾のサブ行列更新に因数分解される。ルックアヘッド技術は、CPUとGPUの作業といくつかの通信をオーバーラップさせるために使用されます。
CPUとGPUの両方のインタフェースでは、考慮すべき行列がGPUメモリに存在し、CPU-GPU転送はパネルのみに関連付けられています。結果の行列は、アルゴリズムの副産物として、計算に沿って蓄積され(必要に応じてマトリックス全体を送信する)、(インタフェースに応じてCPUまたはGPU上に)蓄積される。 CPUインタフェースでは、GPUへの行列の元の転送は、第1のパネルの分解と重複する。この意味では、CPUとGPUインタフェースは類似していますが、通信パターンが異なるため、互いに派生したものではありません。
解のステップは、分解よりO(n)倍少ない浮動小数点演算を行いますが、それを最適化することは依然として非常に重要です。方程式の三角システムを解くことは、計算が帯域幅に制限され、自然に平行ではないため、非常に遅くなることがあります。従来、様々なアプローチが提案されている。 Aの対角ブロックが明示的に反転され、ブロックアルゴリズムで使用されるアプローチを使用します。これは、特に数値的に安定した分解アルゴリズム(例えば、LAPACKおよびMAGMAのような)から得られる三角行列を用いた場合に、高性能の数値的に安定したアルゴリズムをもたらす。
GPUの単精度性能が倍精度性能よりもはるかに高い場合、MAGMAは、混合精度の繰り返し洗練技術に基づいて、第2のソルバーセットを提供します。ソルバーは対応するLU、QR、およびコレスキー因子分解に基づいており、倍精度精度の線形問題を解決するように設計されていますが、はるかに高速な単精度計算に特有の速度です。この考え方は、計算の大部分に単精度を使用すること、すなわち分解ステップを使用し、倍精度算術における単純な反復的な洗練プロセスの前提条件としてその分解を使用することです。これにより、高性能で高精度のソルバが必要になることがよくあります。
Two-sided matrix factorizations
片側行列分解はさまざまな線形ソルバーの基礎であるため、両側行列分解は固有解の基礎となるため、高密度線形代数ルーチンの重要なクラスを形成します。 両面分解は従来、高性能を達成することがより困難でした。 その理由は、両面分解はメモリに束縛された大きな行列ベクトル積を伴い、計算と通信の間のギャップが指数関数的に増加するにつれて、これらのメモリ境界操作はますますボトルネックを処理することがますます困難になるからです。 GPUを加速する魅力的な可能性を提供します。 実際、高帯域幅(例えば、現在のCPUバス帯域幅の10倍)を有するGPUは、マトリックスベクトル生成物を有意に(10~30倍)加速することができる。 ここで、パネル因子分解自体はハイブリッドであり、末尾行列更新はGPU上で実行される。