概要
3次元回転の本を参考に、回転の推定を実装してみた記事です。
点群データ(a1,...,aN)を回転行列Rだけ回転させた点群データ(a'1,...,a'N)があったとします。このとき、回転前と回転後のデータをもとに、Rを推定する手法を実装していきます。今回は、データに等方性誤差が発生している場合の手法をまとめています。等方とは誤差の出方が空間の方向によらないことです。データに誤差が無いときの手法はこちらを参照してください。
手法を2つ紹介しますが、どちらも回転前と回転後の対応する点同士の位置の最小2乗問題を解くことになります。
J=\frac{1}{2}\sum_{\alpha=1}^N||a\prime_\alpha-Ra_\alpha||^2 ...(1)
手法1: 特異値分解を用いた手法
式(1)を展開すると以下のようになります。
J=\frac{1}{2}\sum_{\alpha=1}^N\langle a\prime_\alpha-Ra_\alpha,a\prime_\alpha-Ra_\alpha \rangle\\
=\frac{1}{2}\sum_{\alpha=1}^N(\langle a\prime_\alpha,a\prime_\alpha \rangle-2\langle Ra_\alpha,a\prime_\alpha \rangle+\langle Ra_\alpha,Ra_\alpha \rangle)\\
=\frac{1}{2}\sum_{\alpha=1}^N||a\prime_\alpha||^2 -\sum_{\alpha=1}^N\langle Ra_\alpha,a\prime_\alpha \rangle+\frac{1}{2}\sum_{\alpha=1}^N||a_\alpha||^2...(2)
式(2)を最小化するために、$K$を以下のように置きます。$K$を最大化するRを求めていきます。
K=\sum_{\alpha=1}^N\langle Ra_\alpha,a'_\alpha \rangle...(3)
式(4)が成り立つことを用いると、
\langle a,b \rangle=tr(ab^\intercal)...(4)
$K$は以下のように書けます。
K=tr(R\sum_{\alpha=1}^Na_\alpha a\prime_\alpha^\intercal)=tr(RN)...(5)
ここで$N$は以下のように定義しています。
N=\sum_{\alpha=1}^Na_\alpha a\prime_\alpha^\intercal...(6)
式(3)を最大化する回転Rは、$N$の特異値分解で得られます。今からそれを示していきます。
N=USV^\intercal...(7)
$U$,$V$は直交行列、$S$は以下のような対角行列になります。
S=diag(\sigma_1, \sigma_2, \sigma_3)
σは以下のような大小関係です。
\sigma_1\geq\sigma_2\geq\sigma_3\geq0
式(7)を式(5)に代入すると、次のようになります。
K=tr(RUSV^\intercal)=tr(V^\intercal RUS)=tr(TS)...(8)
途中で、$tr(AB)=tr(BA)$を使っています。また、$T$を以下のように置いています。
T=V^\intercal RU...(9)
$U$と$V$は直交行列で、Rは回転行列(つまり直交行列)なので、$T$も直交行列になります。また、$T=(Tij)$とすると、次のようになります。
tr(TS)=tr\begin{pmatrix}
\begin{pmatrix}
T11 & T12 & T13 \\
T21 & T22 & T23 \\
T31 & T32 & T33 \\
\end{pmatrix}
\begin{pmatrix}
\sigma_1 & 0 & 0 \\
0 & \sigma_2 & 0 \\
0 & 0 & \sigma_3 \\
\end{pmatrix}
\end{pmatrix}\\
=tr
\begin{pmatrix}
\sigma_1T11 & \sigma_2T12 & \sigma_3T13 \\
\sigma_1T21 & \sigma_2T22 & \sigma_3T23 \\
\sigma_1T31 & \sigma_2T32 & \sigma_3T33 \\
\end{pmatrix}\\
=\sigma_1T11+\sigma_2T22+\sigma_3T33...(10)
直交行列は直交する単位ベクトルを行と列とする行列なので、どの要素も大きさが1を超えません。また、$\sigma_1,\sigma_2,\sigma_3\geq0$なので、以下の不等式が成り立ちます。
tr(TS)\leq\sigma_1+\sigma_2+\sigma_3...(11)
等号は$T11=T22=T33=1$で成り立ち、$T=I$(単位行列)を意味します。したがって、式(9)の$T$を$I$にする回転Rが存在すれば、それがKを最大化する回転Rです。
式(9)の$T$を$I$とし、左から$V$、右から$U^\intercal$を掛けると、Rは以下のようになります。
R=VU^\intercal...(12)
$|VU|=1$であれば、$|R|=1$であり、回転行列の性質を満たします。ただし、$V$,$U$は直交行列であり、$|V|=\pm1$, $|U|=\pm1$なので$|VU|=1$とは限りません。
この場合は、式(11)の最小の$σ3$を犠牲にします。
tr(TS)\leq\sigma_1+\sigma_2-\sigma_3...(13)
等号は$T11=T22=1,T33=-1$の時に成り立ちます。Tの行と列は正規直交系なので、$T=diag(1,1,-1)$を意味しています。式(9)の$T$を$diag(1,1,-1)$とし、左から$V$、右から$U^\intercal$を掛けると、Rは次のようになります。
R=V\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
\end{pmatrix}
U^\intercal...(14)
式(12),(14)を合わせて、以下の式が得られます。
R=V\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & |VU| \\
\end{pmatrix}
U^\intercal...(15)
この式は$|VU|=1$のときも$|VU|=-1$のときも$|R|=1$になることがわかります。
ちなみに、$|VU|=-1$の時の拡張は、3次元回転の著者の金谷さんが導き出したそうです。リスペクト。
一連の流れをPythonで実装したものの一部は下のようになります。全部の処理はこちらにあります。
def estimate_R_with_isotropic_errors(ori_norm_arr, rotated_quats_arr):
N = np.dot(ori_norm_arr.T, rotated_quats_arr)
U, s, Vt = np.linalg.svd(N)
V = Vt.T
return np.dot(np.dot(V, np.diag([1, 1, np.linalg.det(V @ U)])), U.T)
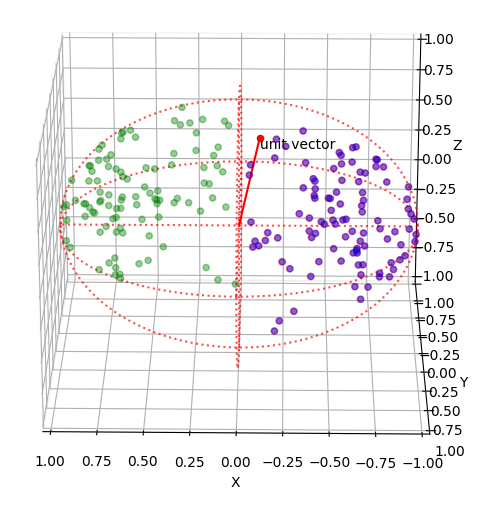
下の画像の青の点群は、緑の点群を赤いベクトルを回転軸として90度回転させ、等方性誤差を付加したものです。
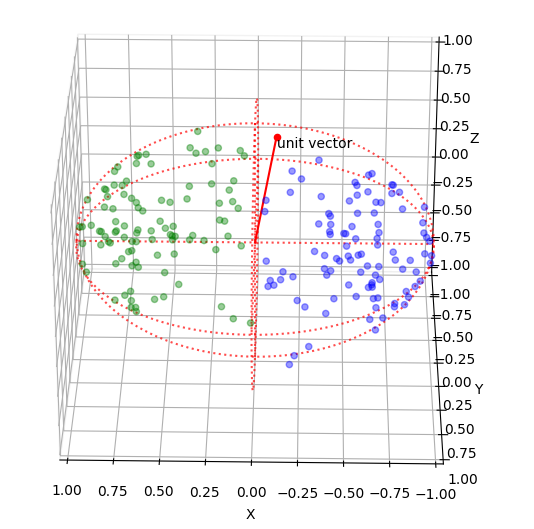
下の画像の赤の点群(青の点群と重ねていて紫っぽくなっている)は、緑と青の点群の位置関係から上記の手法で推定したRを用いて、緑の点群を回転させたものです。 真値の青の点群と重なり、紫色になっていて良い感じになっています。ちなみに対応する点群は、2組あればRを推定することができます。
手法2: クオータニオンを用いた手法
四元数を用いた手法もあります。
詳しい定義などは省きますが、以下のような四元数を用いて、
q=q_0+q_1i+q_2j+q_3k...(16)
Rを以下のように書くことができます。
R=\begin{pmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2) \\
2(q_2q_1+q_0q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1) \\
2(q_3q_1-q_0q_2) & 2(q_3q_2+q_0q_1) & q_0^2-q_1^2-q_2^2+q_3^2 \\
\end{pmatrix}...(17)
式(17)を用いて、$Ra_\alpha$は次のように書くことができます。
Ra_\alpha=\begin{pmatrix}
(q_0^2+q_1^2-q_2^2-q_3^2)a_\alpha(1) + 2(q_1q_2-q_0q_3)a_\alpha(2) + 2(q_1q_3+q_0q_2)a_\alpha(3) \\
2(q_2q_1+q_0q_3)a_\alpha(1) + (q_0^2-q_1^2+q_2^2-q_3^2)a_\alpha(2) + 2(q_2q_3-q_0q_1)a_\alpha(3) \\
2(q_3q_1-q_0q_2)a_\alpha(1) + 2(q_3q_2+q_0q_1)a_\alpha(2) + (q_0^2-q_1^2-q_2^2+q_3^2)a_\alpha(3) \\
\end{pmatrix}
したがって、式(3)の$K$は、次のように書くことができます。
K=\sum_{\alpha=1}^N((q_0^2+q_1^2-q_2^2-q_3^2)a_\alpha(1)a\prime_\alpha(1)+2(q_1q_2-q_0q_3)a_\alpha(2)a\prime_\alpha(1) + 2(q_1q_3+q_0q_2)a_\alpha(3)a\prime_\alpha(1)\\
+2(q_2q_1+q_0q_3)a_\alpha(1)a\prime_\alpha(2)+(q_0^2-q_1^2+q_2^2-q_3^2)a_\alpha(2)a\prime_\alpha(2)+2(q_2q_3-q_0q_1)a_\alpha(3)a\prime_\alpha(2)\\
+2(q_3q_1-q_0q_2)a_\alpha(1)a\prime_\alpha(3)+2(q_3q_2+q_0q_1)a_\alpha(2)a\prime_\alpha(3)+(q_0^2-q_1^2-q_2^2+q_3^2)a_\alpha(3)a\prime_\alpha(3))\\
=\sum_{\alpha=1}^N(q_0^2(a_\alpha(1)a\prime_\alpha(1) + a_\alpha(2)a\prime_\alpha(2) + a_\alpha(3)a\prime_\alpha(3))\\
+q_1^2(a_\alpha(1)a\prime_\alpha(1) - a_\alpha(2)a\prime_\alpha(2) - a_\alpha(3)a\prime_\alpha(3))\\
+q_2^2(-a_\alpha(1)a\prime_\alpha(1) + a_\alpha(2)a\prime_\alpha(2) - a_\alpha(3)a\prime_\alpha(3))\\
+q_3^2(-a_\alpha(1)a\prime_\alpha(1) - a_\alpha(2)a\prime_\alpha(2) + a_\alpha(3)a\prime_\alpha(3))\\
+2q_0q_1(-a_\alpha(3)a\prime_\alpha(2) + a_\alpha(2)a\prime_\alpha(3)) + 2q_0q_2(a_\alpha(3)a\prime_\alpha(1) - a_\alpha(1)a\prime_\alpha(3))\\
+2q_0q_3(-a_\alpha(2)a\prime_\alpha(1) + a_\alpha(1)a\prime_\alpha(2)) + 2q_2q_3(a_\alpha(3)a\prime_\alpha(2) + a_\alpha(2)a\prime_\alpha(3))\\
+2q_3q_1(a_\alpha(3)a\prime_\alpha(1) + a_\alpha(1)a\prime_\alpha(3)) + 2q_1q_2(a_\alpha(2)a\prime_\alpha(1) + a_\alpha(1)a\prime_\alpha(2)))...(18)
式(6)の相関行列$N$の(i,j)要素が$Nij=\sum_{\alpha=1}^Na_\alpha(i) a\prime_\alpha(j)$と書けることを利用すると、式(18)は以下のように書けます。
K=(q_0^2+q_1^2-q_2^2-q_3^2)N11+2(q_1q_2-q_0q_3)N21+2(q_1q_3+q_0q_2)N31\\
+2(q_2q_1+q_0q_3)N12+(q_0^2-q_1^2+q_2^2-q_3^2)N22+2(q_2q_3-q_0q_1)N32\\
+2(q_3q_1-q_0q_2)N13+2(q_3q_2+q_0q_1)N23+(q_0^2-q_1^2-q_2^2+q_3^2)N33\\
=q_0^2(N11+N22+N33)+q_1^2(N11-N22-N33)\\
+q_0^2(-N11+N22-N33)+q_0^2(-N11-N22+N33)\\
+2q_0q_1(-N32+N23)+2q_0q_2(N31-N13)\\
+2q_0q_3(-N21+N12)+2q_2q_3(N32+N23)\\
+2q_3q_1(N31+N13)+2q_1q_2(N21+N12)...(19)
4*4対称行列$N\prime$を以下のように定義すると
N\prime=\begin{pmatrix}
N11+N22+N33 & -N32+N23 & N31-N13 & -N21+N12 \\
-N32+N23 & N11-N22-N33 & N21+N12 & N31+N13 \\
N31-N13 & N21+N12 & -N11+N22-N33 & N32+N23 \\
-N21+N12 & N31+N13 & N32+N23 & -N11-N22+N33
\end{pmatrix}...(20)
4次元ベクトル $q=(q_0,q_1,q_2,q_3)^\intercal$ を用いて、式(19)は次のように書くことができる。
K=\langle q,N\prime q \rangle...(21)
$N\prime$は対称行列なので、式(21)を最大化する$q$は、行列$N\prime$の最大固有値に対する単位固有ベクトルになります。その$q$を式(17)に代入すると、$K$を最大化するRを求めることができます。
コード例は下のようになります。詳細はこちら。
def estimate_R_with_isotropic_errors_by_quaternion(ori_norm_arr, rotated_quats_arr):
N = np.dot(ori_norm_arr.T, rotated_quats_arr)
N_conv = np.array([[(N[0][0] + N[1][1] + N[2][2]), (-N[2][1] + N[1][2]), (N[2][0] - N[0][2]), (-N[1][0] + N[0][1])],
[(-N[2][1] + N[1][2]), (N[0][0] - N[1][1] - N[2][2]), (N[1][0] + N[0][1]), (N[2][0] + N[0][2])],
[(N[2][0] - N[0][2]), (N[1][0] + N[0][1]), (-N[0][0] + N[1][1] - N[2][2]), (N[2][1] + N[1][2])],
[(-N[1][0] + N[0][1]), (N[2][0] + N[0][2]), (N[2][1] + N[1][2]), (-N[0][0] - N[1][1] + N[2][2])],])
w, v = np.linalg.eig(N_conv)
max_vec = v[:, np.argmax(w)]
r = Rotation.from_quat(max_vec[[1, 2, 3, 0]])
return r.as_matrix()
まとめ
金谷さんの本、面白い。