要約Accelerating Sphere Tracing～より良いレイマーチングに向けて Part2～

#はじめに
前回のEnhanced Sphere Tracingの記事を書いている最中、なんとなく被引用論文一覧を眺めていると、この論文で主張されているover-relaxation-sphere-tracingをさらに改良したものに関するペーパーを見つけました。その名もAccelerating Sphere Tracing。この手法を用いるとさらに大胆にωを取れるみたいで、なかなか興味深かったので読みがてら要約してみようと思います。
原文はこちら→https://www.researchgate.net/profile/Csaba_Balint6/publication/331547302_Accelerating_Sphere_Tracing/links/5c7fa522458515831f8814d2/Accelerating-Sphere-Tracing.pdf
ポスター一枚でわかりやすいのでぜひ読んでみてください
##内容
###Previous Method
Over-Relaxation Sphere Tracingについて、詳しくは前回の記事を見てください。簡単に言うと
「距離関数の数値よりもちょっと多めに飛ぶよ、物体を飛び越えちゃったようだったら引き返すよ」
という感じです。
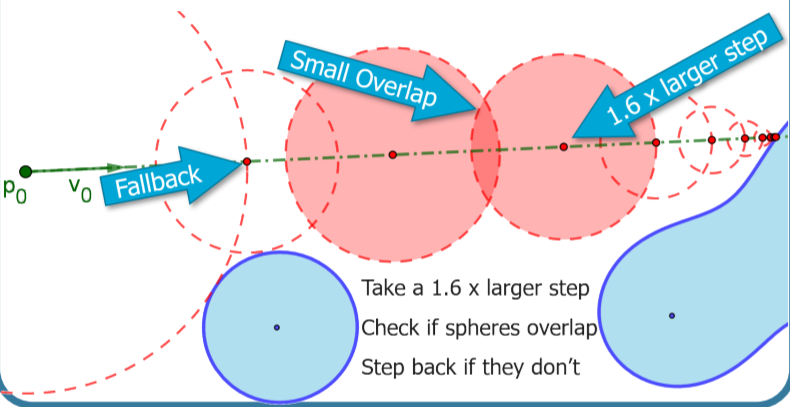
↓通常のSphereTracing

↓Relaxation Sphere Tracing、SDFの値の1.6倍遠くへ進み、飛び越したっぽかったら引き返す。

###提案手法
Enhanced Sphere TracingのResultでも述べられていたようにこの手法にはまだ洗練の余地がある、ということでこのペーパーではもう少し厳密に跨ぎ越したかどうかの判定をすることで、レイの各ステップをもうちょっと大胆に飛べるようにしたものです。従来のものだとω（距離関数に乗算する倍率）は1~2に限定されており、オブジェクトを飛び越えたかどうかの判定は、
距離関数を

x∊R^3,f(x)∊R

各ステップにおけるレイの先端の位置を

p_1,p_2,...,p_n∊R^3

で表すと

f(p_{n-1}) + f(p_{n}) < length(p_n - p_{n-1})

で行います（上記の不等式が成り立つとき飛び越えているとみなす）。今回の手法では単純に1.ω倍だけレイを伸ばすのではなく二つ手前のsdfの結果まで用いることで「物体が平面であった場合の次のsdfの値」を予測し、現在のsdfの値に加えその0.x倍だけレイを伸ばす作業を行います。

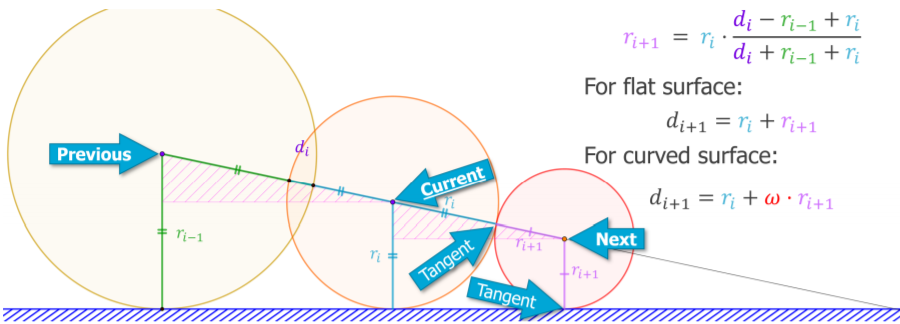
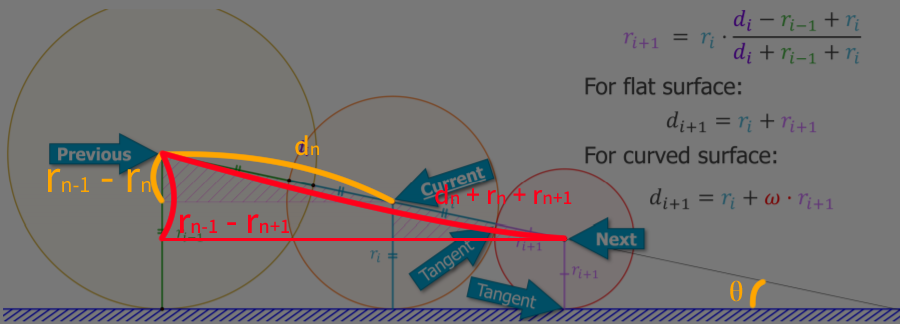
上の図を見るとわかるように、SDFによって得られる半径の円は常に曲面（図の場合は平面）に接する円だよねってアイデアをもとにしているみたいです。
この手法を用いることでステップごとの距離は伸び、引き返す回数も減ります。具体的に見てみましょう。
##提案手法の数学的な解説
i回目のステップにおける実際の移動距離を

d_1,d_2,...,d_n

で表す、つまり

d_n = length(p_{n} - p_{n-1})

であるとする。まずレイ近辺の物体が平面であると考えたとき、引き返しの条件式である

f(p_{n-1}) + f(p_{n}) < length(p_n - p_{n-1})

をギリギリ満たさないような(つまり間にオブジェクトが入らないと考えられるギリギリ)の位置を予測する。交差判定をとる物体が平面であると仮定すると、

レイ上の物体平面と「p_nを中心とした半径f(p_n)の円」両方に接する点

が上記の条件を満たす点であり、次のレイの最も効率の良い行き先（予測）である。実際に欲しいのは「どれだけレイを伸ばせばよいのか」なので

レイ上の物体平面と「p_nを中心とした半径f(p_n)の円」両方に接する円の半径 = r_{n+1}

を求めることにする。レイと平面がなす角のサインは

sin\theta = \frac{d_n}{r_{n-1} - r_n}

で表すことが出来る。

次に $ r_{n+1} $ に関する方程式を立てる。

sin\theta = \frac{d_n + r_n + r_{n + 1}}{r_{n-1} - r_{n+1}}

これに先ほどの$sin\theta$を代入して$r_{n+1}$について解くと以下の解が得られる。

r_{n+1} = \frac{d_n-r_{n-1}+r_n}{d_n+r_{n-1}+r_n}

よって次にレイがステップできる最適な距離は

d_{n+1} = r_n+r_{n+1}

となる（通常のSphereTracing分とこれまでの式で算出した追加分）。ただし、これは交差判定を取るオブジェクトが平面であった場合の予想であった。例えばオブジェクトが凹形状だった場合、上記の$d_{n+1}$だと次のレイの移動先はオブジェクト内に入り込んでしまう。そうするとレイは引き返さなくてはならず、余計な動作をしてしまうので、余裕を持たせるためにステップの距離を少なめにとることにしよう。

d_{n+1} = r_n + \omega  r_{n+1},\omega\in(0,1)

つまり0~1の間の数値を掛けることで少しゆとりを持たせることにする、ということだ。これでもオブジェクトのめり込み、飛び越えが発生した時は従来と同じように

 \omega  r_{n+1}

分だけ引き返し、通常のSphereTracingと同じだけ進む。
これを通常のSphereTracingと同様に繰り返して$f(p_n)$が一定の値より小さくなったタイミングでそこを交差点とみなす。

##結果

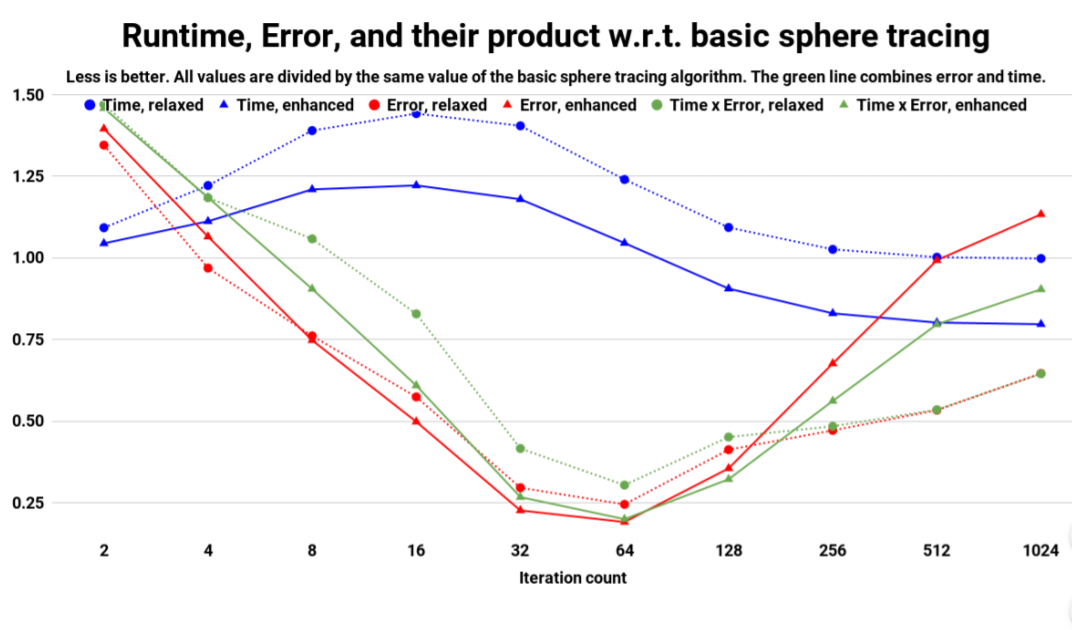
元のポスターによると、従来のRelaxation Sphere Tracingよりも約0.8倍ぐらいの時間でレンダリングすることが可能になったみたいです。すごい。

#最後に
この論文が発表されたのが2018年なので、SphereTracingはまだまだ改良の余地がありそうな感じがしてワクワクしますね。僕もなんかいい感じの改良を発見してチヤホヤされて～～～～～