初めに
この前参加したShader優秀若者肉会にて"Enhanced Sphere Tracing"なる論文の存在を教えてもらったので確認したところ、英語だったので本腰入れて読むついでにざっくりと要約していこうと思います。
原文はこちら→http://erleuchtet.org/~cupe/permanent/enhanced_sphere_tracing.pdf
原文には実装例も載っているので是非目を通してみてください。
以下要約
Abstract
この論文は従来のSphereTracingを動作速度や描画クオリティ的に向上させる以下の手法を提案するものである。
- 過伸長法を用いたスフィアトレーシング
- スクリーンスペースを考慮した交差点の選択
- 自己交差を防ぐために動的にεを設定する
- 非連続性の軽減
- 凸形状の物質に対する最適化
Introduction
スフィアトレーシングはSDFを用いた立体表現のレンダリングに用いられる手法である。本論文ではスフィアトレーシングを用いた際に直面する動作速度的、描画の質的な制約を突破するための実装可能な手法を提案する。
Enhancing Sphere Tracing
従来のスフィアトレーシングについて今一度確認しよう。実数の3次元ベクトルから実数への射影f
f:R^3 \rightarrow R
が以下の条件を満たすときそのfを符号付距離境界(signed distance bound)と呼ぶ。ただし、
f ^{-1} (0)
を関数が示す陰関数曲面とし、
dist(x,f^{-1}(0))
をxと陰関数曲面の距離とする。
f(x) \leq \left\{
\begin{array}{ll}
-dist(x,f^{-1}(0)) & (x inside of f^{-1}(0)) \\
+dist(x,f^{-1}(0)) & (x outside of f^{-1}(0))
\end{array}
\right.
右辺と左辺に等号が成り立つときこれを符号付距離関数(SignedDistanceFunction)と呼ぶ。
スフィアトレーシングでは原点をo,パラメータtを用いてレイを以下のように表現する。
r(t) = d*t + o
(ただしdはレイの方向を示す3次元実ベクトル)
スフィアトレーシングは
f(r(t)) = 0
なるtを求めるアルゴリズムであるといえる。
ある漸化式pを以下のように定める。ただしpは3次元実ベクトルである。
p_0 = 0 \\
p_{i + 1} = p_i + d * f(p_i)
つまりある点から曲面への距離分レイをdの方向に伸ばすことを1回分の操作とする。これを繰り返すことでレイはどんどん伸びていき、最終的に物質の交差点で止まることが知られており、その際のpが交差点を表す座標である。
Over Relaxation Sphere Tracing
レイトレーシングにおいて、
p_{i + 1} = p_i + d * f(p_i) * ω
のωに(0,1]の実数を入れた場合もレイマーチングとして成立することが知られている。今回はさらにレイを伸ばす回数を削減するために、ωに[1:2)の実数を代入することを考える。こうすることで一つのステップにおいて通常のレイマーチングより多くのレイが伸びることとなる。それと同時にωが1より大きくなることでレイの間の物質をまたぎ越してしまうパターンが生じてしまう。これに対して物体を跨いだかどうかの判定を行い、跨いでいることが発覚した時は引き返すようにしよう。跨ぎ判定は
|f(p_{i - i})| + |f(p_i)| < d * f(p_i) * ω
によって行われる。つまりレイを伸ばす前と後のオブジェクトとの距離の和がそのステップの歩幅より小さければ間にオブジェクトが挟まっていたことを示している。
次に引き返す際の歩幅だが、
p_{fallback} = p_i + d * \delta_{i - 1} * (1 - \omega )
とする。この分引き返せば実質的にω=1分進んだのと等価になる。
↓上が従来のSphereTracing、下が提案手法。黄色い円で跨ぎ越しを検知して1ステップ前に戻し、ω=1分のステップを行っている(黄色い円と矢印の向いている円の間にある円)
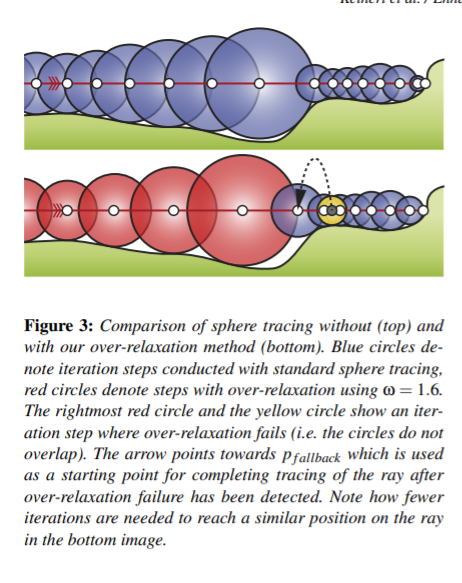
スクリーンスペースを考慮した交差点の選択
レイがオブジェクトのギリギリを掠めて、交差しない場合を考えよう。オブジェクトのギリギリを掠めるとき、レイの歩幅が極端に小さくなる部分が出来てしまい、その結果レイの進行が中空(オブジェクトほど近くなく、掠めなかったレイほど遠くない位置)で終わってしまう場合がある。こういった場合オブジェクトの周辺にオーラみたいな靄が発生してしまう場合がある。
↓右上の画像に意図しないアウトラインが描画されているのがわかる。右下のが提案手法によって修正されたもの。
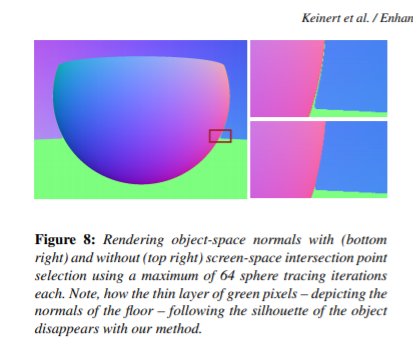
一般的にはレイのステップ数を増やせばこれらの靄は消える傾向にあるが、いくらレイを増やしてもこれらを完全に消すことは出来ないし、そもそも処理速度的にもステップ数は最小に抑えたい。
そこで本手法ではレイが物体と交差しなかった時、従来のようにレイの最後のステップを用いるのではなく、スクリーンから見て最も物体に近づいたときのレイを利用する。また、スクリーンから見た物体とレイの距離がピクセル間の距離の半分になったタイミングでレイの行進を終了する。これによって描画精度に影響を与えることなく靄を消し、無駄なレイの進行を打ち切ることが出来る。
↓レイが掠めたときの例。赤い円がスクリーンスペースで最も小さいので、このレイがどことも交差しなかった場合はこれが採用される。
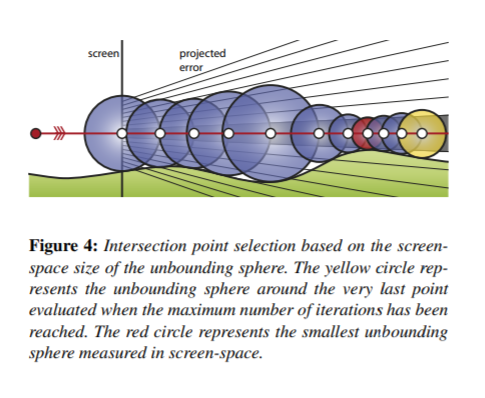
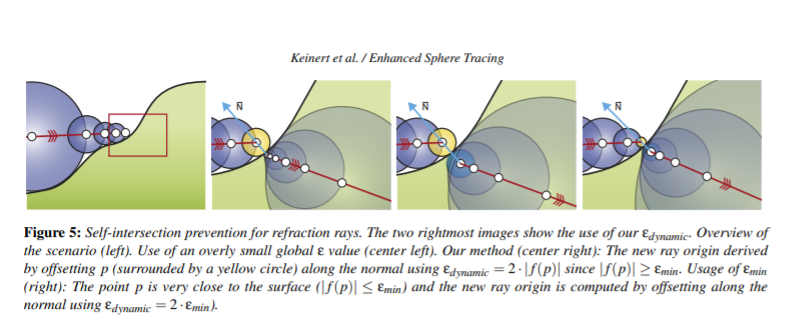
自己交差を防ぐためのεの動的設定
反射や屈折を表現する際に(反射方向に)飛ばす2度目のレイが飛ばした瞬間に接触判定(距離<ε)を満たしてしまう現象とその回避法はよく研究されてきたものである。一般的な場合は2度目のレイの原点をレイの来た方向や法線方向に微小量だけずらすことで解決可能だが、スフィアトレーシングでは実際の物体の表面とレイと物体の交差点が離れてしまうことが多い(特にεによる繰り返しの打ち切りをしている場合は)ため、上記の処置では不適切な可能性が出てくる。
本手法では固定のεを用いるのではなく、各交差点に応じて動的にεを設定することによってこれらの問題を回避する。
\epsilon_{dynamic} = 2max(\epsilon_{min},|f(p)|)
でεを設定する。この際に、
\epsilon_{min}
を設定する必要があるのだが、これを適切に大きい数にすることによって、f(x)が0に近い場合に発生する諸問題(精度起因の問題、交差点周辺で無駄にレイのステップが増大する問題など)を解消することが出来る。レイを伸ばした時点で既にf(x)は計算済みのはずなので動的にεを算出するコストは十分小さいと考えられる。
非連続性の緩和
一般的なスフィアトレーシングにおける有限回のレイ伸長操作と定数εによる繰り返しの打ち切りでは、ある(スクリーン上の)ピクセルから発射され長距離を移動したレイは隣のピクセルから発射されたレイとかなりの距離(非連続性)を持ってしまう。その結果としてスクリーンに表示される画像には意図しない波みたいなものが発生することがある(下図右上参照)

これを防ぐために描画に影響が出ないようなレベルで交差判定を妥協することにする。この手法では従来の
f(p) = 0
の代わりに
f(p) = err(||p_i - o||_2)
を満たすようなxを目指すようにレイを伸ばすことにする。ここで
err(||p_i - o||_2)
は原点とレイの先端のスクリーンスペース上の距離をもととして許容できる誤差を示す関数である。(これに関しての具体的な実装例はEfficient antialiased rendering of 3-D linear fractalsから引用されている)つまり、レンダリング結果には影響を及ぼさない範囲で甘めに衝突判定をする、ということであり、その誤差をスクリーンスペースで取っているということはレイが奥に行くにつれて許容できる誤差は大きくなるということである。これらの処理によって描画精度を落とさないようにレイのステップ数を減らすことができ、それによって上記の非連続性に起因する意図しない描画を防ぐことが出来る。
この改良を加えたレイの進行処理は以下のようになる。
p_{i + 1} = p_i + d*(f(p_i) - err(||p_i - o ||_2))
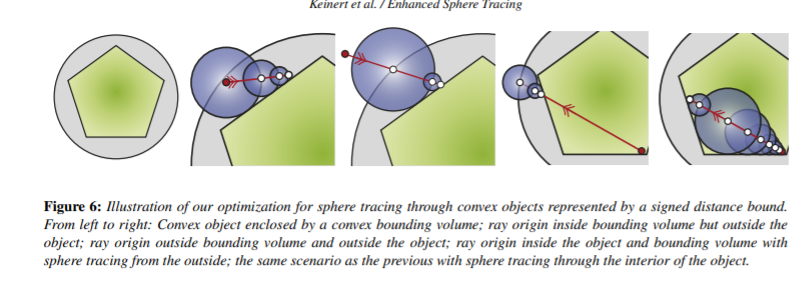
凸形状物質における最適化
レイの起点がオブジェクトの内側に入ってしまうことを考える。この時、レイが物質の内側でステップ数を無駄に増やしてしまう場合がある。そこで、物質に一回り大きい境界を設けることでそれを回避する方法を考える。
レイの原点がオブジェクトの内側にあるとき、レイを外側の一回り大きい境界まで伸ばし、そこから逆方向にレイを進めることで無駄なステップなく交差判定を取ることが出来るようになる。
↓一番右が物体内で無駄にステップしている例。右から2番目が提案手法。
Result
実装の結果これらの手法は最適化や描画精度の改良に大きなメリットがあった。over-relaxation-sphere-tracingに関してはもう少し洗練する余地がありそうなのと、現在は手動で決めているωに関しては最適な数値になるようにオートマチックに決定できる機構の研究が今後の課題になりそう、とのこと。
おわり
迂闊に訳し始めたら結構な作業量になってしまいました。何か間違っているところがあったら教えてほしいです。