Juliaで球体の光散乱問題を解く

モチベーション

大学での研究で，ナノ粒子の散乱特性をよく計算します．以前はMatlabを用いていましたが，適当に書いたプログラムの遅さが気になるようになってきました．元々実験屋さんなので，あまりプログラムを最適化するのに時間をかけたくない，ベクトル化が面倒，と思っていた時に，Juliaが早いよという噂を聞きました．いざ実践．

プログラムの概要

球体に光（平面波）を照射した際の応答は，1908年にGustav Mieにより厳密解が与えられました．Mie理論と呼ばれるこの理論式を計算するプログラムをJuliaで書きます．
この問題は文献[Craig F. Bohren Donald, R. Huffman, "Absorption and Scattering of Light by Small Particles"][ref.1] (以下B&H) に詳しく解説されています．理論の詳細は気が向いたら別記事を書くとして，ここでは割愛します．
実際に実装した式は，B&Hのeq.(4.52-4.53) にあるMieのa,b係数の導出と，eq.(4.61) の散乱効率の導出がメインとなります．まず計算に必要なパラメータを定義します．球の半径を$a$，球の屈折率を$N_1$，媒質の屈折率を$N$，計算したい波長を$\lambda_0$とします．この時，波数は$k=2\pi/\left(\lambda_0/N\right)$であり，波長に対する粒子のサイズを表すサイズパラメータ ($x$) は$x=ka$で与えられます．これと，媒質に対する球の屈折率 ($m$) を$m=N/N_1$を用いて，Mieのa,b係数は以下の式で与えられます．
$$a_n=\frac{m^2j_n\left(mx\right)\left[xj_n\left(x\right)\right]^\prime-j_n\left(x\right)\left[mxj_n\left(mx\right)\right]^\prime}{m^2j_n\left(mx\right)\left[xh_n^{\left(1\right)}\left(x\right)\right]^\prime-h_n^{\left(1\right)}\left(x\right)\left[mxj_n\left(mx\right)\right]^\prime}$$

$$b_n=\frac{j_n\left(mx\right)\left[xj_n\left(x\right)\right]^\prime-j_n\left(x\right)\left[mxj_n\left(mx\right)\right]^\prime}{j_n\left(mx\right)\left[xh_n^{\left(1\right)}\left(x\right)\right]^\prime-h_n^{\left(1\right)}\left(x\right)\left[mxj_n\left(mx\right)\right]^\prime}
$$
ここで，$j_n\left(\rho\right)$は球ベッセル関数，$h_n^{\left(1\right)}\left(\rho\right)$は第一種球ハンケル関数，プライム (') は一次微分を表します．
これらの係数は，それぞれ$n$次の電気多極子 (TM) ・磁気多極子 (TE) 共鳴モードの寄与を示しており，散乱断面積は以下で与えられます．
$$Q_{sca}=\frac{x^2}{2}\sum_{n=1}^{\infty}{(2n+1)(\left|a_n\right|^2+\left|b_n\right|^2)}$$

これら以外に，a,b係数を用いると，球外部での任意の散乱電場・磁場を求めることができるため，放射パターンなども実装します．

プログラムはGitHubで公開しています．JuliaのMie理論パッケージなので，jlmieと命名しました．
https://github.com/Hinamoooon/jlmie

環境構築

• Windows 10 Pro 64 bit

Juliaの環境構築から初めます．エディタはVS Codeを利用します．Juliaのインストールは特に問題なく進みました．
VS Codeはインストール済みの環境で，https://julialang.org/からJulia v1.5.3 64bit (installer)をダウンロードし，インストール．VS Codeの拡張機能Julia（julialang.language-julia）をインストールすると，エディタ内からShift+Enterで走るようになりました．

Mie理論の実装

ベッセル関数の計算には，Juliaの特殊関数パッケージ (SpecialFunctions) を用い，球ベッセル関数・ハンケル関数等は適当に定義しました．

# spherical bessel functions
sbesselj(nu, x) = √(π./2x)*besselj.(nu+1/2, x)
sbessely(nu, x) = √(π./2x)*bessely.(nu+1/2, x)
shankelh1(nu,x) = sbesselj.(nu,x) + 1im.*sbessely.(nu,x)

Mieのa,b係数は以下のように関数化して呼び出します．

function jlmie_abcd(m,x,n::Int)
# calculate n-th order Mie coefficients a,b,c,d
# input:
# m: relative refractive index (n_material / n_environment)
# x: size parameter (wavenumber * radius)

    # Bessel/Hankel functions
    jx = sbesselj.(n,x)
    jmx = sbesselj.(n,m.*x)
    hx = shankelh1.(n,x)

    # derivative
    d1xjx = x.*sbesselj.(n-1,x) .- n.*sbesselj.(n,x)
    d1mxjmx = m.*x.*sbesselj.(n-1,m.*x) .- n.*sbesselj.(n,m.*x)
    d1xhx = x.*shankelh1.(n-1,x) .- n.*shankelh1.(n,x)
    
    an = (m.^2 .*jmx.*d1xjx .- jx.*d1mxjmx) ./
         (m.^2 .*jmx.*d1xhx .- hx.*d1mxjmx)
    bn = (jmx.*d1xjx .- jx.*d1mxjmx) ./
         (jmx.*d1xhx .- hx.*d1mxjmx)
    cn = (jx.*d1xhx .- hx.*d1xjx) ./
         (jmx.*d1xhx .- hx.*d1mxjmx)
    dn = (m.*jx.*d1xhx .- m.*hx.*d1xjx) ./
         (m.^2 .*jmx.*d1xhx .- hx.*d1mxjmx)
    return an,bn,cn,dn
end

最終的に，散乱効率は$m$,$x$を用いて，以下で計算します．

function jlmie_Qsca(m,x,nmax::Int=-1)
# Calculate scattering efficiency of a sphere
# Input:
# m: relative refractive index (n_material / n_environment)
# x: size parameter (wavenumber * radius)
# namx: maximun order of resonances being considered
#       (nmax = 1: dipole, 2: dipole+quadrupole, ...,
#        -1: sufficiently large value determined by x)
# Output:
# Qsca: Scattering efficiency (total up to n-th order resonances)
    if nmax == -1
        nmax = largenmax(x)
    end

    Qsca = zeros(length(x))
    for i = 1:nmax
        Qsca = Qsca .+ jlmie_Qsca_n(m,x,i)
    end
    return Qsca
end

function jlmie_Qsca_n(m,x,n::Int)
    an,bn,_,_ = jlmie_abcd(m,x,n)
    nth_Qsca = 2 ./ x.^2 .* (2*n+1).*(abs.(an).^2 .+ abs.(bn).^2)
    return nth_Qsca
end

2つ目の関数jlmie_Qsca_n()が$n$次の散乱効率を計算する式です．これを$n=1$から$n=nmax$まで足し合わせることで，散乱効率としています．¹
その他詳細は公開しているソースをご覧ください。

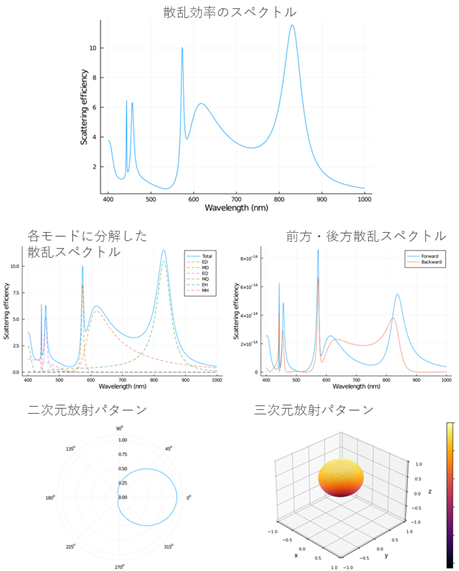
色々なプロットをしてみました．三次元のサーフェスプロットが微妙です．

パッケージ化

Juliaの練習を兼ねて適当に書いたプログラムですが，一応誰でも使えるようにパッケージ化を行いました．
JuliaにはPkgTemplatesという便利なものがあるようで，先人の知恵をお借りして，以下のサイトを参考にさせていただきました．

• PkgTemplates による Julia パッケージの作り方（前半）
• Juliaのパッケージ開発に便利なPkgTemplates, Revise, developコマンド
  
• Juliaにおけるパッケージ管理＆新しいパッケージ作成メモ
• Juliaの開発環境構築

まずPkgTemplatesをインストールし，以下のコードを記述したファイルを実行し，テンプレートを作成しました．

using PkgTemplates

t = Template(;
      user="Hinamoooon",
      authors=["Tatsuki Hinamoto"],
      dir="(パッケージを配置したい場所)",
      plugins=[
        Git(; ssh=false),
        License(; name="MIT"),
        GitHubActions(),
        Documenter{GitHubActions}(),
        TravisCI(),
        GitHubPages(),
    ],
)

generate("jlmie", t)

続いて，ソースファイルの場所等を適当に変更，関数の呼び出し方やグラフ化等を示すExampleファイルを色々作成，Readme.mの記述等々を行って，パッケージの体裁を整えました．また，Juliaのパッケージマネージャーを利用して，jlmieが依存しているSpecialFunctions等のパッケージをProject.tomlに書き込みました（上記サイト参照）．testの作成には「Juliaの開発環境構築」を参考にしました．そしてGitHubに同名のリポジトリを作成し，GitHub DesktopのAdd existing repository...からGitHubにpushしました．
一点，PkgTemplateの使い方でよくわからなかったのは，自動的に ".jl" がリポジトリ名の後ろに付くことです．何となくつけたくなかったのですが，やり方がわからず，テンプレート作成後に，ファイル内の "jlmie.jl" を手作業で "jlmie" に変更しました（./.gitの中も修正しないといけなかった記憶があります）．
何とか上手くパッケージ化ができ，以下のコマンドで誰でも使えるようになりました．

(@v1.5) pkg> add https://github.com/Hinamoooon/jlmie.git

まとめ

普段はMATLABを利用しているのと，Pythonを少し齧っていましたが，Juliaにはスムーズに移行できそうです．ベクトル化しなくても早いプログラムが書けますが，初回実行時のプリコンパイルに時間がかかるので，一長一短でしょうか．
Juliaの利用を通じて，逆にMATLABの良さも見えてきました．やはりJuliaは日本語の情報量がまだまだ少なく，必要十分な量の情報がきちんとオーガナイズされているMATLABの公式Documentationが恋しくなります．

Reference

1. Absorption and Scattering of Light by Small Particles; Bohren, C. F., Huffman, D. R., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998.

1. namxは，デフォルトで十分大きな値まで計算するようになっています．この値はlargenmax()という別関数で定義しており，B&HのAppendix. Aにあるように，サイズパラメータの関数で$n_max = x+4x^{1/3}+2$で与えられます．
   ↩