N.Mです。今回はふとWebGLで陰関数モデルのレンダリングを行う際に、こういう方法はできるのかと自由研究を行いました。その際にWebGLやシェーダ周りでいくつか知見があったので、記事にまとめてみました。
導入
陰関数モデルとは
そもそも陰関数モデルとは何かですが、簡単に言うとモデルの形状を3次元空間上の位置(x, y, z)を引数にとる関数で表すモデルのことです。ある位置でこの関数の値が負であれば、その位置はモデルの内側に、正であればモデルの外側にあることになります。
例えば原点を中心にとる半径rの球であれば、$ f(x, y, z) = \sqrt{x^2 + y^2 + z^2} - r $と表現されます。
一般的なレンダリング手法
このような陰関数モデルを描画する際はよくマーチングキューブ法やレイマーチング法が使用されます。1
マーチングキューブ法
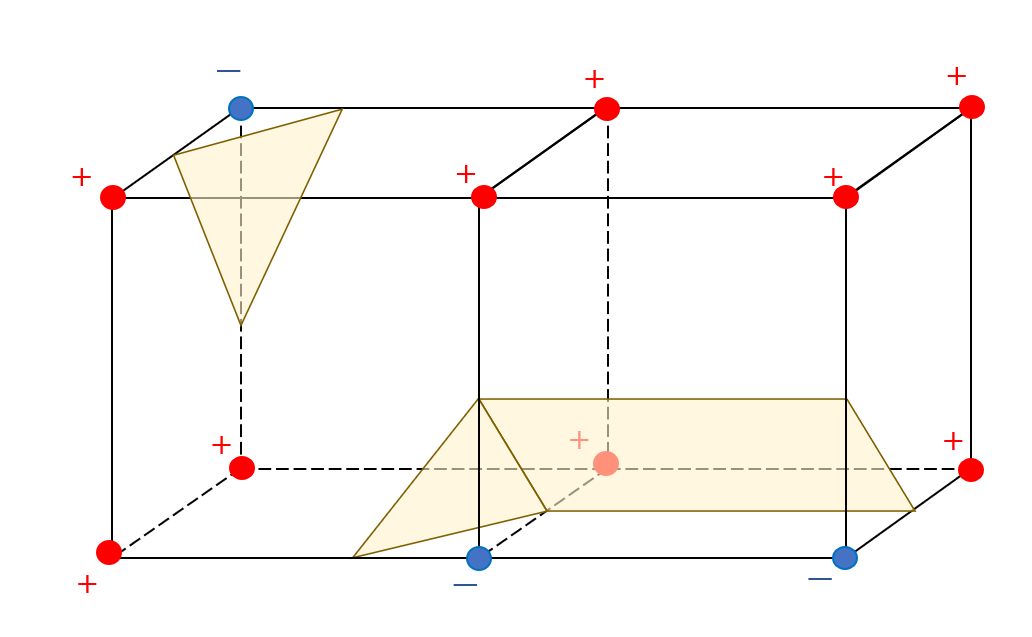
まず3次元空間を格子状に分割し、各格子点での陰関数の値を計算します。その後、格子点で囲まれる立方体を対象に等値面メッシュを構成するポリゴンを決定していきます。
図のように各格子点での値の符号にもとづいて、ポリゴンを生成していきます。
この手法はポリゴンさえ生成できてしまえば、等値面メッシュの描画処理は軽いという利点があります。しかし、格子が粗いと等値面メッシュも粗くなったり、全立方体に対してポリゴンを生成する処理が重いという欠点があります。
WebGLでマーチングキューブ法を実装したという記事がQiitaにもあり、WebGLでの実装はすごいなと思いました。
ただ、格子点の符号のパターンごとに分岐が必要だったり、その符号のパターンをシェーダに送るのに工夫が必要だったりと、実装が複雑になりそうです。
レイマーチング法
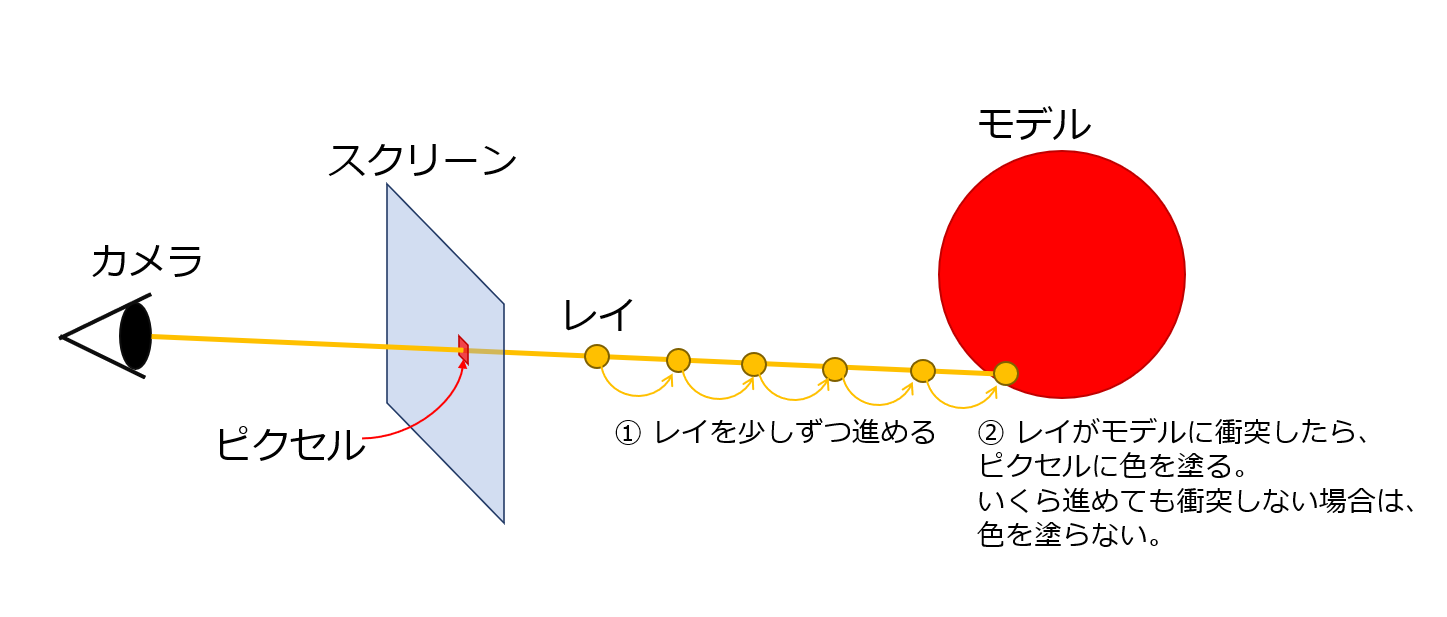
カメラからスクリーンのピクセルに向かって光線(レイ)を飛ばし、レイと物体(モデル)との衝突情報をもとにピクセルの色を決めるレイトレーシングの一種です。レイマーチングではレイを少しずつ移動し、移動した点でその都度陰関数を計算することで、レイが衝突したかを調べます。
レイマーチングではポリゴンでの近似はせず、スクリーンの各ピクセルに対し処理するため、球のようなスムーズな曲面を描画できます。しかし、各ピクセルに対し処理を行うため、工夫をしないと処理が重くなってしまいます。
今回試してみたかったレンダリング手法:マーチングキューブレイ
今回試してみたかった手法は、マーチングキューブ法とレイマーチング法を足して2で割ったような手法です。勝手にマーチングキューブレイ (Marching Cube Ray) と名づけます。処理は以下のような流れです。
- 空間を格子上に分割し、格子点ごとに陰関数の値を計算する。
- 格子点で囲まれる立方体のポリゴンをシェーダに送る。
- 立方体全体が陰関数のモデルの外側にある場合は、最適化のために頂点シェーダで除外する。
- 立方体をフラグメントシェーダで描画する際に、カメラからのレイを計算する。立方体とレイとの衝突点を開始地点としてレイを少しずつ移動させ、立方体内でレイマーチングを行う。
- レイが陰関数モデルと衝突するならば、ピクセルの描画や深度値の書き込みを行い、そうでなければピクセルを透明にし深度値も無効にする。
格子内立方体をバウンディングボックスみたいに扱って、その立方体内でのみレイマーチングするイメージですね。
この方法なら立方体が描画される範囲に限定してレイマーチング処理を実行できるため、処理を軽くしつつ、スムーズな曲面を描画できそうだと思いました。また、実際に書いたシェーダもシンプルなものになりました。(フラグメントシェーダで90行程度)
この記事で触れること
-
今回のレンダリング手法の実装、最適化で得られた知見
- 3Dテクスチャ
- 頂点シェーダでの描画省略
- フラグメントシェーダでの深度値書き込み
この記事で触れないこと
-
シェーダなどWebGLの基礎概念や使い方の解説
こちらはwgld.orgが参考になると思います。
頂点バッファオブジェクトや頂点シェーダ、フラグメントシェーダと聞いてピンと来ない方はwgld.orgもご覧いただけると理解が深まるかと思います。 -
ソースコードの数学的な解説
こちらは以下のの記事で解説しています。
[自由研究] WebGL2で陰関数モデルをレンダリングしてみた の補足
実行環境
CPU:Intel Core i7-13700H 2.40GHz
RAM:32.0GB
GPU:NVIDIA GeForce RTX 4060 Laptop GPU
2
また、実装ではWebGL2を使用しております。
デモ、ソースコード
マーチングキューブレイの手法で超二次楕円体をレンダリングするデモです。
超二次楕円体については過去の記事でも触れているので、興味のある方はご覧ください。
右側のコントローラでモデルの形状や色、光の向きを変更できます。キャンバスの画素は1280px × 720pxで、格子は64×64×64で分割しています。上記の実行環境では画面いっぱいにモデルを表示しない限りは、60fpsで動いているようでした。
今回の記事では、ポイントとなる部分をピックアップして解説するので、実際に描画するまでに必要な処理のいくつかは解説を割愛します。全体としてどのように実装しているか気になる方は、以下のリポジトリをご覧ください。
GitHubリポジトリ
実装の詳細
頂点バッファ
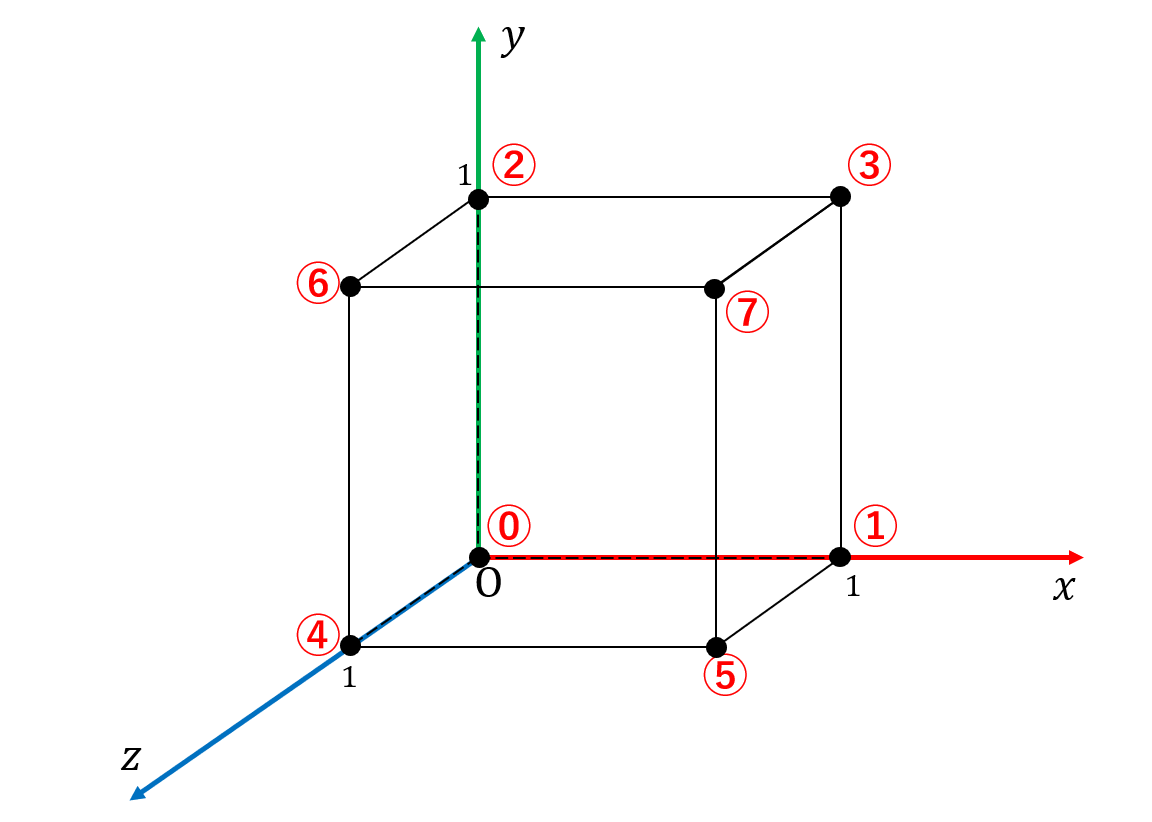
格子点を囲む立方体の頂点に対し、以下の図の丸数字のようにインデックスをつけています。隣接する格子では共通の格子点が出てきますが、別々の立方体の頂点として扱うために、別々の頂点として作成しています。
WebGLでは頂点インデックスの型がunsigned shortで、すべての立方体頂点を一度に描画しようとするとインデックスの最大値制限にひっかかるため、頂点データを何回か分けて描画できるようにしています。
var bufferInfo = {
position_vbo: null,
position_data: null,
cubePos_vbo: null,
cubePos_data: null,
cubeBase_vbo: null,
cubeBase_data: null,
ibo: null,
index_num: 0
};
// 中略
function createCubeBuffer() {
// (全頂点)÷(頂点バッファオブジェクトに含める頂点数)の分だけ、配列の要素を作る。
const maxCubeNumInOneVbo = 64 * 64;
const vboNum = Math.round(Math.pow(cubeInfo.num, 3)) / maxCubeNumInOneVbo;
bufferInfo.position_data = new Array(vboNum);
bufferInfo.cubePos_data = new Array(vboNum);
bufferInfo.cubeBase_data = new Array(vboNum);
// 各要素は頂点バッファオブジェクトのデータ分だけ入るFload32Arrayを準備する。
const vboDataNum = maxCubeNumInOneVbo * cubeBasePosition.length;
for (var vboIdx = 0; vboIdx < vboNum; vboIdx++) {
bufferInfo.position_data[vboIdx] = new Float32Array(vboDataNum);
bufferInfo.cubePos_data[vboIdx] = new Float32Array(vboDataNum);
bufferInfo.cubeBase_data[vboIdx] = new Float32Array(vboDataNum);
}
var cubeIdx = 0;
var vboIdx = 0;
// 中略
for (var z = 0; z < cubeInfo.num; z++) {
for (var y = 0; y < cubeInfo.num; y++) {
for (var x = 0; x < cubeInfo.num; x++) {
// 頂点バッファオブジェクトに送るデータの作成(後述)
cubeIdx++;
// 頂点バッファオブジェクトの頂点数を超えたら、次の配列にデータを格納していく。
if (cubeIdx >= maxCubeNumInOneVbo) {
cubeIdx = 0;
vboIdx++;
}
}
}
}
bufferInfo.position_vbo = create_vbo(bufferInfo.position_data[0], true);
bufferInfo.cubePos_vbo = create_vbo(bufferInfo.cubePos_data[0], true);
bufferInfo.cubeBase_vbo = create_vbo(bufferInfo.cubeBase_data[0], true);
// インデックスバッファオブジェクトの作成(割愛)
}
また、シェーダでカメラからのレイを計算したり、関数値を取得できるように、立方体の頂点ごとに2つのベクトルを付与し、頂点位置とともに頂点バッファオブジェクトに送ります。
-
cubePos... 図の立方体の原点(⓪の頂点)から見た際の、頂点の位置 -
cubeBase... 格子内における立方体原点の位置
var cubeInfo = {
size: 0.2,
num: 64
};
// 中略
var cubeBasePosition = [
0.0, 0.0, 0.0,
1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
1.0, 1.0, 0.0,
0.0, 0.0, 1.0,
1.0, 0.0, 1.0,
0.0, 1.0, 1.0,
1.0, 1.0, 1.0,
];
// 中略
function createCubeBuffer() {
// 中略
var cubeIdx = 0;
var vboIdx = 0;
const cubeVertexNum = cubeBasePosition.length / 3;
const entireSize = cubeInfo.num * cubeInfo.size;
for (var z = 0; z < cubeInfo.num; z++) {
for (var y = 0; y < cubeInfo.num; y++) {
for (var x = 0; x < cubeInfo.num; x++) {
var basePos = [
x * cubeInfo.size - entireSize * 0.5,
y * cubeInfo.size - entireSize * 0.5,
z * cubeInfo.size - entireSize * 0.5
];
var xyz = [x, y, z];
// 頂点バッファオブジェクトに送るデータの作成
for (var cIdx = 0; cIdx < cubeVertexNum; cIdx++) {
var currentMemHead = cubeIdx * cubeBasePosition.length + cIdx * 3;
for (var xyzIdx = 0; xyzIdx < xyz.length; xyzIdx++) {
// position
bufferInfo.position_data[vboIdx][currentMemHead + xyzIdx]
= basePos[xyzIdx] + cubeBasePosition[cIdx * 3 + xyzIdx] * cubeInfo.size;
// cubePos
bufferInfo.cubePos_data[vboIdx][currentMemHead + xyzIdx]
= cubeBasePosition[cIdx * 3 + xyzIdx];
// cubeBase
bufferInfo.cubeBase_data[vboIdx][currentMemHead + xyzIdx]
= xyz[xyzIdx] / cubeInfo.num;
}
}
cubeIdx++;
// 頂点バッファオブジェクトの頂点数を超えたら、次の配列にデータを格納していく。
if (cubeIdx >= maxCubeNumInOneVbo) {
cubeIdx = 0;
vboIdx++;
}
}
}
}
// 中略
}
陰関数のデータを送る手段:3Dテクスチャ
WebGL2から3Dテクスチャの機能が使えるので、下記の記事を参考に3Dテクスチャに陰関数モデルの関数値を格納するように実装しました。3
ICS MEDIA / WebGL 2.0 - TEXTURE_3Dでボリュームレンダリング表現を行う
今回、テクスチャに格納する値は通常のテクスチャで使用するような0~255の値ではなく、float型である必要があるため、以下のようなコードで浮動小数点テクスチャを有効にします。これにより、テクスチャのフォーマット指定でRGBA32Fが使用可能となります。
g_gl=c.getContext('webgl2');
if (!g_gl) {
g_gl.getExtension("EXT_color_buffer_float");
}
3Dテクスチャの場合も2Dテクスチャと同じような形でテクスチャを作成できます。
中間での補間について、wgld.orgの記事によるとNEARESTにしないとレンダリング時にエラーが出るようなので、NEARESTにします。こちらとしても勝手に値を補間されると困るので好都合ですね。
下記のcreateFunctionValueTextureではテクスチャのメモリ確保や設定だけ行い、実際のデータはまだ入れていません。
var cubeInfo = {
size: 0.2,
num: 64
};
// 中略
var textureInfo = {
functionValue_tex: null,
functionValue_data: null
};
// 中略
function createFunctionValueTexture() {
textureInfo.functionValue_tex = g_gl.createTexture();
g_gl.activeTexture(g_gl.TEXTURE0);
g_gl.bindTexture(g_gl.TEXTURE_3D, textureInfo.functionValue_tex);
g_gl.texStorage3D(g_gl.TEXTURE_3D, 1, g_gl.RGBA32F,
cubeInfo.num + 1, cubeInfo.num + 1, cubeInfo.num + 1);
g_gl.texParameteri(g_gl.TEXTURE_3D, g_gl.TEXTURE_MAG_FILTER, g_gl.NEAREST);
g_gl.texParameteri(g_gl.TEXTURE_3D, g_gl.TEXTURE_MIN_FILTER, g_gl.NEAREST);
g_gl.texParameteri(g_gl.TEXTURE_3D, g_gl.TEXTURE_WRAP_S, g_gl.CLAMP_TO_EDGE);
g_gl.texParameteri(g_gl.TEXTURE_3D, g_gl.TEXTURE_WRAP_T, g_gl.CLAMP_TO_EDGE);
g_gl.texParameteri(g_gl.TEXTURE_3D, g_gl.TEXTURE_WRAP_R, g_gl.CLAMP_TO_EDGE);
}
実際の3Dテクスチャの中身は以下のupdateFunctionValueTextureで作成しています。
zyxで3重ループを回し、RGBAの各チャンネルに値を記録します。
陰関数の偏微分値4は、フラグメントシェーダでモデルの法線を決定する際に使用します。
- R... xで陰関数を偏微分した値
- G... yで陰関数を偏微分した値
- B... zで陰関数を偏微分した値
- A... 陰関数の値
function updateFunctionValueTexture() {
const entireSize = cubeInfo.num * cubeInfo.size;
const epsilon = 0.0001;
textureInfo.functionValue_data = new Float32Array(Math.round(Math.pow(cubeInfo.num + 1, 3)) * 4);
var vertIdx = 0;
for (var z = 0; z <= cubeInfo.num; z++) {
for (var y = 0; y <= cubeInfo.num; y++) {
for (var x = 0; x <= cubeInfo.num; x++) {
var basePos = [
x * cubeInfo.size - entireSize * 0.5,
y * cubeInfo.size - entireSize * 0.5,
z * cubeInfo.size - entireSize * 0.5
];
textureInfo.functionValue_data[4 * vertIdx] = (functionValue(basePos[0] + epsilon, basePos[1], basePos[2])
- functionValue(basePos[0] - epsilon, basePos[1], basePos[2])) / (2.0 * epsilon);
textureInfo.functionValue_data[4 * vertIdx + 1] = (functionValue(basePos[0], basePos[1] + epsilon, basePos[2])
- functionValue(basePos[0], basePos[1] - epsilon, basePos[2])) / (2.0 * epsilon);
textureInfo.functionValue_data[4 * vertIdx + 2] = (functionValue(basePos[0], basePos[1], basePos[2] + epsilon)
- functionValue(basePos[0], basePos[1], basePos[2] - epsilon)) / (2.0 * epsilon);
textureInfo.functionValue_data[4 * vertIdx + 3] = functionValue(basePos[0], basePos[1], basePos[2]);
vertIdx++;
}
}
}
g_gl.texSubImage3D(g_gl.TEXTURE_3D, 0, 0, 0, 0, cubeInfo.num + 1, cubeInfo.num + 1,
cubeInfo.num + 1, g_gl.RGBA, g_gl.FLOAT, textureInfo.functionValue_data);
}
3Dテクスチャを使用する場合、後述する頂点シェーダ、フラグメントシェーダではsampler3D型の変数でテクスチャの値を読み取ります。しかし、sampler3Dはデフォルトでは精度の指定がないため、シェーダでprecision mediump sampler3D;のように明示的に精度の指定をする必要があります。
頂点シェーダ
頂点シェーダでは、モデル変換、ビュー変換、プロジェクション変換を経た頂点位置を計算します(ここは通常の頂点シェーダでも見かける処理だと思います)。また、頂点バッファオブジェクトに渡したcubePosやcubeBaseをフラグメントシェーダに中継しています。
この頂点バッファで特筆すべき点は、 描画する必要のない立方体の場合は頂点を画面外に飛ばす点 です。こうすることでフラグメントシェーダでその立方体についての処理が行われなくなり、負荷軽減になります。
立方体の全頂点がモデルの外側にある場合、シェーダ内のshouldDrawCubeは0.0を返すようにしています。(そうでなければ1.0を返します。)
shouldDrawCubeの値が0.0の場合はmix関数でgl_PositionにinvalidVertexPosが代入されるようにしています。invalidVertexPosを必ず画面外になるような点にすれば、描画する必要のない立方体の頂点は画面外に飛ぶという流れです。
次のフラグメントシェーダでもそうですが、stepやmax, mixを駆使することで、if分岐を使わずに分岐っぽい処理を書くことができました。step関数については、以下の記事でも触れられていたので、少し参考にしています。
条件分岐のためにstep関数を使う時の考え方をまとめてみた
export default `#version 300 es
precision mediump float;
precision mediump sampler3D;
in vec3 position;
in vec3 cubePos;
in vec3 cubeBase;
uniform mat4 mvpMatrix;
uniform mat4 mvMatrix;
uniform mat4 mvMatrixTranspose;
uniform float cubeNum;
uniform sampler3D functionValueTexUnit;
uniform float isosurfaceValue;
out vec4 vPosition;
out vec3 vCubeBase;
out vec3 vRayOrigin;
out vec3 vRayDirection;
float shouldDrawCube(vec3 iCubeBase) {
float cubeNumInv = 1.0 / cubeNum;
float result = 0.0;
vec4 v000 = texture(functionValueTexUnit, iCubeBase + vec3(0.0, 0.0, 0.0) * cubeNumInv);
vec4 vx00 = texture(functionValueTexUnit, iCubeBase + vec3(1.0, 0.0, 0.0) * cubeNumInv);
vec4 v0y0 = texture(functionValueTexUnit, iCubeBase + vec3(0.0, 1.0, 0.0) * cubeNumInv);
vec4 vxy0 = texture(functionValueTexUnit, iCubeBase + vec3(1.0, 1.0, 0.0) * cubeNumInv);
vec4 v00z = texture(functionValueTexUnit, iCubeBase + vec3(0.0, 0.0, 1.0) * cubeNumInv);
vec4 vx0z = texture(functionValueTexUnit, iCubeBase + vec3(1.0, 0.0, 1.0) * cubeNumInv);
vec4 v0yz = texture(functionValueTexUnit, iCubeBase + vec3(0.0, 1.0, 1.0) * cubeNumInv);
vec4 vxyz = texture(functionValueTexUnit, iCubeBase + vec3(1.0, 1.0, 1.0) * cubeNumInv);
result = max(result, 1.0 - step(isosurfaceValue, v000.w));
result = max(result, 1.0 - step(isosurfaceValue, vx00.w));
result = max(result, 1.0 - step(isosurfaceValue, v0y0.w));
result = max(result, 1.0 - step(isosurfaceValue, vxy0.w));
result = max(result, 1.0 - step(isosurfaceValue, v00z.w));
result = max(result, 1.0 - step(isosurfaceValue, vx0z.w));
result = max(result, 1.0 - step(isosurfaceValue, v0yz.w));
result = max(result, 1.0 - step(isosurfaceValue, vxyz.w));
return result;
}
void main(void) {
vec4 invalidVertexPos = vec4(-1000.0, -1000.0, 1.0, 1.0);
vPosition = mvpMatrix * vec4(position, 1.0);
vCubeBase = cubeBase;
vRayOrigin = cubePos;
vRayDirection = (mvMatrixTranspose * mvMatrix * vec4(position, 1.0)).xyz;
gl_Position = mix(invalidVertexPos, vPosition, shouldDrawCube(cubeBase));
}
`
フラグメントシェーダ
フラグメントシェーダで立方体内でレイマーチングの処理を行い、ピクセルの色を決めます。また、ここでは レイと陰関数モデルが衝突しない場合、ピクセルに無効な深度値を書き込む ことをしています。5
WebGL2からピクセルの色だけでなく、深度値の書き込みもできるようになったようです。
【WebGL2】gl_FragDepthを使ってフラグメントシェーダーで深度を書き込む
レイと陰関数が当たっていない場合、ポリゴンの該当するピクセルの色は透明になりますが、その際に深度値を無効にしないと、ポリゴンの位置の深度で深度値が記録されてしまい、この後にポリゴンよりも奥の立方体を描画しようとした際に深度テストで弾かれてしまいます。
立方体をカメラから見て奥から手前に描画するようソートしているなら問題ありませんが、ソートしていないので、視点によって描画結果がおかしくなります。
このフラグメントシェーダではレイと陰関数モデルが衝突しない場合はgl_FragDepthに1.0(最も奥の値)を書き込むことで、後続のポリゴンが深度テストで必ず弾かれない無効な深度値にしています。
以下は今回のフラグメントシェーダです。
頂点シェーダと同じく、stepやmax, mixを駆使することでif文分岐を除去でき、コードも90行程度とシンプルなものになりました。
フラグメントシェーダ内の処理は数学的な解説が必要な部分が多いですが、こちらは以下の別の記事にまとめます。コメントアウトにおおまかに何をしているかは書いておきます。
[自由研究] WebGL2で陰関数モデルをレンダリングしてみた の補足
export default `#version 300 es
precision mediump float;
precision mediump sampler3D;
uniform mat4 mvMatrixTranspose;
uniform float cubeNum;
uniform sampler3D functionValueTexUnit;
uniform float isosurfaceValue;
uniform vec4 globalColor;
uniform vec3 lightDir;
in vec4 vPosition;
in vec3 vCubeBase;
in vec3 vRayOrigin;
in vec3 vRayDirection;
out vec4 outFlagColor;
float trilinearInterpolation(vec3 pos, vec4 currentFuncValueMinusZ, vec4 currentFuncValuePlusZ) {
vec3 oneMinusPos = vec3(1.0) - pos;
return oneMinusPos.y * oneMinusPos.z * (oneMinusPos.x * currentFuncValueMinusZ.x + pos.x * currentFuncValueMinusZ.y)
+ pos.y * oneMinusPos.z * (oneMinusPos.x * currentFuncValueMinusZ.z + pos.x * currentFuncValueMinusZ.w)
+ oneMinusPos.y * pos.z * (oneMinusPos.x * currentFuncValuePlusZ.x + pos.x * currentFuncValuePlusZ.y)
+ pos.y * pos.z * (oneMinusPos.x * currentFuncValuePlusZ.z + pos.x * currentFuncValuePlusZ.w);
}
void main(void) {
const float infinity = 10000.0;
const float epsilon = 0.0001;
const int divideNum = 8;
const int iterNum = 24;
// 立方体の各頂点での関数値、偏微分値をテクスチャから取得する。
float cubeNumInv = 1.0 / cubeNum;
vec4 v000 = texture(functionValueTexUnit, vCubeBase + vec3(0.0, 0.0, 0.0) * cubeNumInv);
vec4 vx00 = texture(functionValueTexUnit, vCubeBase + vec3(1.0, 0.0, 0.0) * cubeNumInv);
vec4 v0y0 = texture(functionValueTexUnit, vCubeBase + vec3(0.0, 1.0, 0.0) * cubeNumInv);
vec4 vxy0 = texture(functionValueTexUnit, vCubeBase + vec3(1.0, 1.0, 0.0) * cubeNumInv);
vec4 v00z = texture(functionValueTexUnit, vCubeBase + vec3(0.0, 0.0, 1.0) * cubeNumInv);
vec4 vx0z = texture(functionValueTexUnit, vCubeBase + vec3(1.0, 0.0, 1.0) * cubeNumInv);
vec4 v0yz = texture(functionValueTexUnit, vCubeBase + vec3(0.0, 1.0, 1.0) * cubeNumInv);
vec4 vxyz = texture(functionValueTexUnit, vCubeBase + vec3(1.0, 1.0, 1.0) * cubeNumInv);
vec4 funcValueMinusZ = vec4(v000.w, vx00.w, v0y0.w, vxy0.w);
vec4 funcValuePlusZ = vec4(v00z.w, vx0z.w, v0yz.w, vxyz.w);
vec4 funcNormalXMinusZ = vec4(v000.x, vx00.x, v0y0.x, vxy0.x);
vec4 funcNormalXPlusZ = vec4(v00z.x, vx0z.x, v0yz.x, vxyz.x);
vec4 funcNormalYMinusZ = vec4(v000.y, vx00.y, v0y0.y, vxy0.y);
vec4 funcNormalYPlusZ = vec4(v00z.y, vx0z.y, v0yz.y, vxyz.y);
vec4 funcNormalZMinusZ = vec4(v000.z, vx00.z, v0y0.z, vxy0.z);
vec4 funcNormalZPlusZ = vec4(v00z.z, vx0z.z, v0yz.z, vxyz.z);
// レイが立方体に入る地点から出ていく地点までの距離を計算している。
vec3 rayOrigin = clamp(vRayOrigin, 0.0, 1.0);
vec3 rayDirection = normalize(vRayDirection);
float maxT = infinity;
for (int idx = 0; idx < 3; idx++) {
float signDir = step(0.0, rayDirection[idx]);
float candidateT = mix(rayOrigin[idx], 1.0 - rayOrigin[idx], signDir) / (abs(rayDirection[idx]) + epsilon);
maxT = min(maxT, mix(infinity, candidateT, step(epsilon, abs(rayDirection[idx]))));
}
maxT = mix(0.0, maxT, step(epsilon, abs(infinity - maxT)));
maxT = max(maxT, 0.0);
// ここでレイ上の点を立方体に入る地点から少しずつ動かすことでレイと陰関数モデルの衝突点を探している。
// (レイマーチングの処理)
vec3 currentRayPos = rayOrigin;
float invDivideNum = 1.0 / float(divideNum);
float oneStepT = maxT * invDivideNum;
float currentT = 0.0;
float hitFlag = 0.0;
for (int idx = 0; idx < iterNum; idx++) {
float currentValue = trilinearInterpolation(currentRayPos, funcValueMinusZ, funcValuePlusZ) - isosurfaceValue;
float currentSign = step(0.0, currentValue);
hitFlag = max(hitFlag, 1.0 - currentSign);
currentT -= mix(oneStepT, 0.0, currentSign);
oneStepT *= mix(invDivideNum, 1.0, currentSign);
currentT = clamp(currentT + oneStepT, 0.0, maxT);
currentRayPos = clamp(rayOrigin + currentT * rayDirection, 0.0, 1.0);
}
// レイと陰関数モデルとの衝突点での法線を計算
vec3 surfaceNormal;
surfaceNormal.x = trilinearInterpolation(currentRayPos, funcNormalXMinusZ, funcNormalXPlusZ);
surfaceNormal.y = trilinearInterpolation(currentRayPos, funcNormalYMinusZ, funcNormalYPlusZ);
surfaceNormal.z = trilinearInterpolation(currentRayPos, funcNormalZMinusZ, funcNormalZPlusZ);
surfaceNormal = normalize(surfaceNormal);
// 計算された法線をもとにライティングのDiffuse成分やSpecular成分を計算
vec3 lightDirInCube = normalize((mvMatrixTranspose * vec4(lightDir, 0.0)).xyz);
float diffuse = max(dot(lightDirInCube, surfaceNormal), 0.0);
vec3 refRayDirection = rayDirection + 2.0 * dot(surfaceNormal, - rayDirection) * surfaceNormal;
float specular = pow(max(dot(refRayDirection, lightDirInCube), 0.0), 5.0);
// ピクセルの色や深度値の書き込み。レイと陰関数モデルが衝突しない場合は、ここまでhitFlagが0.0のままであるため、
// 深度値は最も奥にある扱いとなる1.0が書き込まれる。
outFlagColor = min(0.2 + diffuse, 1.0) * globalColor + specular * vec4(1.0);
gl_FragDepth = mix(1.0, vPosition.z / vPosition.w, hitFlag);
outFlagColor.a = mix(0.0, 1.0, hitFlag);
}
`
まとめ
今回、陰関数で表現されたモデルをレンダリングするために、マーチングキューブレイの手法を試しに実装してみました。
スペックが高めのPCで実行しているとはいえ、Webブラウザ上できれいな球などを60fpsで描画できており、割と実用性のありそうな手法だと我ながら思いました。また、格子をポリゴンで表現しているため、ほかのポリゴンモデルと共存する形で描画することもできそうかと思いました。
問題点としては、超2次楕円体のパラメタを小さくすると、以下の画像のように形状がギザギザになってしまったり、法線も正しくないためかまだらなライティングになってしまう点が挙げられます。これは立方体内の関数値を単純なトリリニア補間でやっている影響もあるかと考えております。偏微分の値も考慮するような補間方法であれば改善しそうかと思います。
また、複数の格子をまたがるようなレイの追跡はできないため、現状は反射や屈折をこの手法で計算することはできないかと思います。良い改善方法を思いついたら、試してみたいですね。(変な線みたいなものが出てしまう問題などもあるので、試す際に修正したいです。)
今回の実装でWebGL2の機能を初めて使用してみたり、if分岐を使わない書き方を考えたりしてみて、意外とWebGLのシェーダでもいろいろなことができそうだと思いました。また、ほかに面白いものを思いついたら、実装してみたいです。
-
マーチングテトラヘドラ法やスフィアトレーシングのように、マーチングキューブ法やレイマーチング法の派生となる手法も存在します。 ↩
-
余談ですが、今年ようやく新しいゲーミングノートPCを新調しました。 ↩
-
3Dテクスチャを使用しないのであれば、関数値を頂点バッファオブジェクトに送ることになりますが、各頂点で立方体の全頂点分の関数値や偏微分値が必要になり、複数の頂点バッファオブジェクトが追加で必要になります。 ↩
-
偏微分については、偏微分の値がその点で不連続である可能性も考慮し、xyzそれぞれの成分について左側微分と右側微分を計算し、その平均をとるようにしています。 ↩
-
昔のWebGLで
gl_FragDepthが使用できない場合はdiscardでピクセルを破棄するという方法があり、最初はそれで対応しましたが、処理が分岐するためか、負荷が高くなってしまいました。 ↩