はじめに
はじめまして,N.Mと申します.
今慶應義塾大学学部4年で卒業研究の実装にはまっている身なのですが,ずっと同じことばかりしても飽きてきてしまうので,飽きないように息抜きで初投稿です.
今回は今年6,7月にDelphiで実装したレイトレーサについての話です(luxideaさんに指導していただいたり,ライブラリを提供していただいてます.本当にありがとうございました).以下のスライド,ソースと一緒に記事をご覧ください.
スライド
ソース
Delphiのアドベントカレンダーの企画をluxideaさんに紹介してもらい,スライドとソースだけでも良いから投稿してと勧められたのですが,それだけだとつまらないと思ったので補足とかも交えながら,いろいろ書こうかと思います.Delphiというよりかはレイトレーサといった理論的な話が多くなってしまいますがご了承ください.

↑今回作った画像(サイト用にすこし画質は落としてます).クリスマスオーナメントに使えそう,使えそうじゃない?
レイトレーシング
みなさんご存じだと思いますが,画素に向かってレイを飛ばし,画素に向かう光がどの物体に当たって反射したものか追跡して画素の色を決める手法です(スライドの3ページ目参照).表面の頂点位置をパラメタを用いたりして明示的に与えてポリゴンを張る陽的(explicit)なモデルに対して,表面の頂点情報は与えられておらず立体を陰関数として表現した陰的(implicit)なモデルを描画するのに向いている低速だけど高品質に描画できるレンダリング手法です.
#超2次楕円体
上の画像の一番左の列から左から5番目の列までに表示された形状のことです.パラメタを変えることで球をはじめ角が取れたような立方体,円柱等を表現できます.式はスライドの2ページ目に書いていますが,小数の累乗が出てくるなど解析的な観点から見ると複雑な式です.
問題点
レイトレーサで描画するにはレイと物体との当たり判定,言い換えると直線と立体との当たり判定が必要です.球といった簡単な立体の場合は立体の式を用いて方程式をたてて,それを解いて交点を求めるという感じで最初は超2次楕円体についてもそれでやろうとしました.超2次楕円体の場合,小数の累乗を含む方程式になり,解析的に解くことは困難なのでニュートン法を用いて解こうとしましたが下のように穴が空いちゃったり,描画できてなかったりと失敗しました.

レイトレーサではカメラ中心に最も近い直線と立体との交点が必要で,ニュートン法ではそれが安定してできなかったんですね・・・
#そのための改善策,あとそのためのスフィアトレーシング・・・?
そこでluxideaさんに教えて頂いたのがスフィアトレーシングです.簡単にどういう手法か説明すると,直線上の点(Pとします)をカメラ中心に配置し,各立体表面からPまでの距離を計算.その最短距離だけPを直線上に沿って進めるということを点Pの位置が収束するまで繰りかえす方法で,この方法だと安定して直線と立体とのカメラ中心に最も近い交点を求めることができました.さらに,方程式を解く必要はなく表面からの距離(しかも厳密な距離じゃなくても距離より必ず小さくなる尺度なら可)を求めれば良く,新しい立体もその距離を計算する関数を組むだけで簡単に追加できます.またブーリアン演算(スライド10ページ目)も簡単に実装できました.
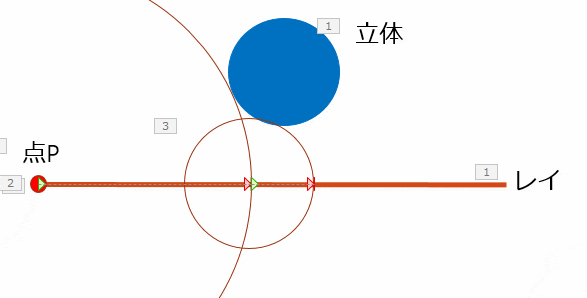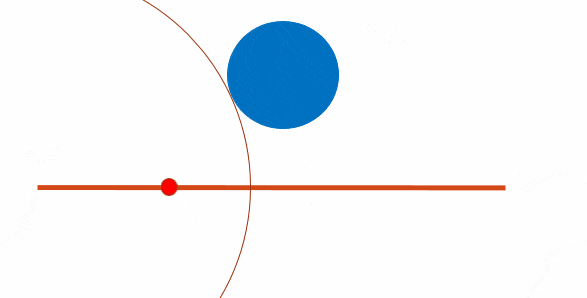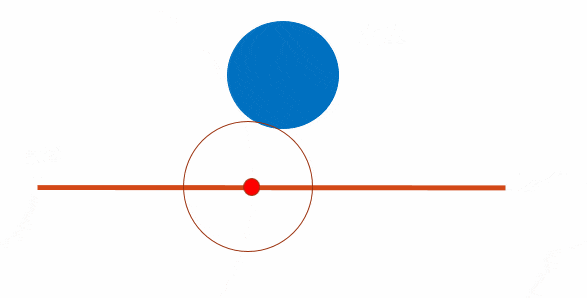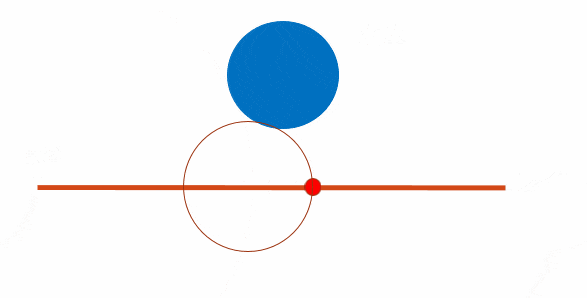
↑スライドの5ページ目にも載っけたスフィアトレーシングを説明するアニメーション

↑ブーリアン演算を実行した例.立方体と球について左からOr,And,Minusの演算を行ったもの.一番最初の画像の正八面体,正十二面体,正二十面体も平面のAndをとって作ってます.
超2次楕円体の距離関数
スライドの8~9ページに書いたように超2次楕円体の式を距離関数として用いました.luxideaさんに教えてもらったこの論文を参考にしています.
Delphiでの実装
RAD StudioにはTImageという画像パーツがあるようなので,レイトレーシングのアルゴリズムで決定した画素の色をそれに書き込めば良いようです.RAD Studioでないと画像表示するにもC/C++だったらOpenCVとか入れないと1から画像表示をさせるのは大変なのでRAD Studio様様です.あとその他実装について詳しいことはソースをご覧ください.
こんな感じに今回はDelphiでもレイトレーサが作れるよというお話でした.最後までお付き合い頂きありがとうございました.