一次元データで単純な閾値による異常検知
y0<-rep(0,100)
x1<- rnorm(100,50,8)
plot(x1,y0,xlim=c(10,80))
こんなデータが取得できたとする。
データはすべて異常を含まないデータとすると、このデータすべてを認める閾値を決めて、
閾値を超えるような値は異常と判別してやればいい。
このデータを学習用データとして考える。
abline(v=mean(x1))
abline(v=mean(x1)+sd(x1)*3,col="red")
abline(v=mean(x1)-sd(x1)*3,col="red")
たとえばこの赤線を閾値として設定してやれば、次に来たデータが
mean(x1)-sd(x1)*3 < data < mean(x1)+sd(x1)*3
の範囲であれば正常
超えていれば異常と言える。
例として3σ区間で赤線を引いたが、
plotした学習用データすべてが正常であるということが前提であるため、
学習用データのとり得る値によって正常と見なす範囲をずらしてもいい。
こうして学習用データから異常の判別モデルとしての閾値が求められた。
一次元データから確率を閾値とする場合
先ほどのデータからは単純に閾値を求めるものだった。
今回のデータは正規分布に従っている。
つまり、データ点ごとの確率値を求めることができる。
実際にイメージしやすいよう、データ点ごとを確率密度関数にかけたものをplotしてみる。
正規分布の確率密度関数の式はネットに転がっているのでそちらを参照されたい。
過去に正規分布の理解方法についての記事も書いているので、そちらにものせている。
p_each_point <- dnorm(x1,mean(x1),sd(x1))
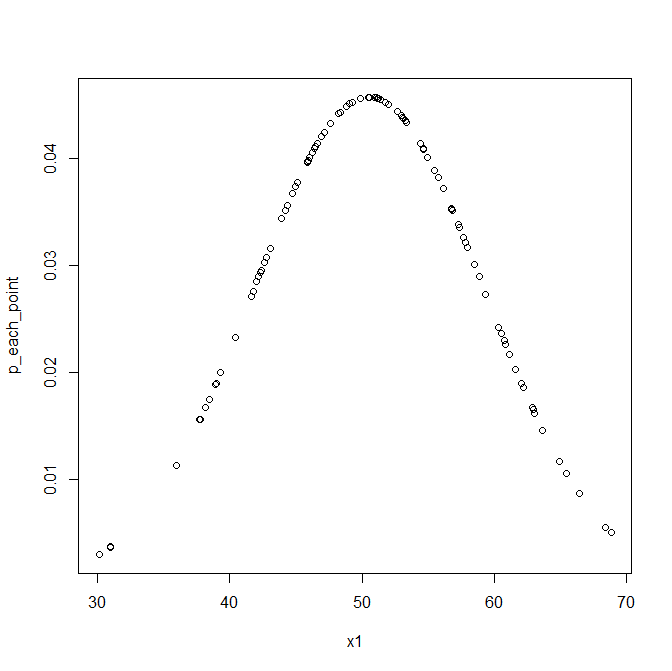
plot(x1,p_each_point)
今回のデータ各点を入力の値として、さらにデータから得られた平均と標準偏差をパラメータとして作成した、
正規分布の確率密度関数から計算された確率の値は図のようになる。
y軸が、ある平均値meanと標準偏差sdを持つとき、x座標の値が入力されたときに返ってくる確率値である。
中心はy軸の値が大きく、離れるほど低い値となっている。
先ほどはx軸の値を閾値とした。
しかし今回は確率密度関数から確率値がもとめられたので、これを判断基準としてみよう。
例えば中心から最も離れている点の確率値を確認してみよう。
> min(p_each_point)
[1] 0.001305687
もっとも低い値は0.0013という確率であった。
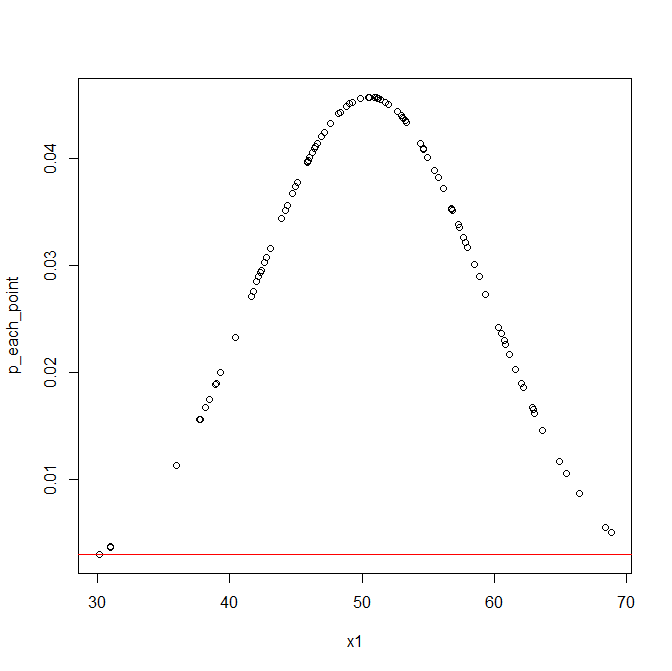
この値を判断基準とする場合は図で示すとこうなる。
abline(h=min(p_each_point), col="red")
これよりも下回る確率をとるような値は異常であり、
この閾値よりも上に来るような値は正常であると考えられる。
最初にやったx軸の値で上限下限を決めるような判定方法とほとんど一緒。
しかしこの下で説明する多変量の時には少しばかり優秀な働きをする。
学習用データから平均と標準偏差というパラメータを求めて、
確率値を密度関数から計算して、判別モデルとなる閾値を決定した。
多変量であったら
データが一次元ならば上記のように考えたが、多変量のデータであったらどうするか?
par(mfrow=c(2,1))
x1<- rnorm(100,50,8)
M1=mean(x1)
SDx1<-sd(x1)
plot(x1,y0,xlab="",ylab="",xlim=c(0,200))
abline(v=mean(x1)+sd(x1)*4,col="red")
abline(v=mean(x1)-sd(x1)*4,col="red")
x2<- rnorm(100,100,20)
M2=mean(x2)
SDx2<-sd(x2)
plot(x2,y0,xlab="",ylab="",xlim=c(0,200))
abline(v=mean(x2)+sd(x2)*4,col="red")
abline(v=mean(x2)-sd(x2)*4,col="red")
こんな閾値を変数毎に求めて、変数一つ一つについて閾値を超えていないかチェックする?
そんなことをしなくても密度関数で閾値をきめてやたら一つの閾値だけで求まりそう。
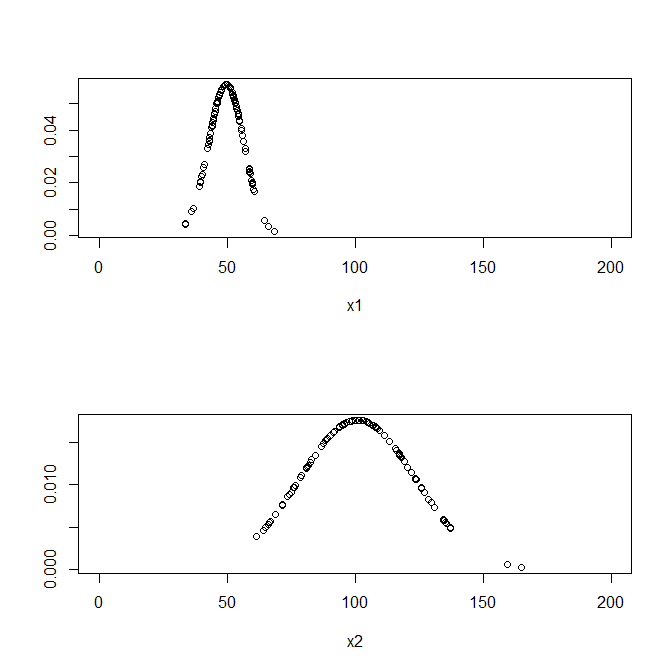
par(mfrow=c(2,1))
data_p_x1<-dnorm(x1,mean(x1),sd(x1))
plot(x1,data_p_x1,ylab="",xlim=c(0,200))
data_p_x2<-dnorm(x2,mean(x2),sd(x2))
plot(x2,data_p_x2,ylab="",xlim=c(0,200))
> min(c(data_p_x1,data_p_x2))
[1] 0.001020142
この確率を下回るようなデータは異常だと検知できる。
積事象として考えてplotしてみる
二次元データから確率値を計算し、plotしようとすると三次元になる。
お互いに独立で同一の瞬間から発生したデータだと考えると、積事象として確率が考えられるので、
確率は掛け算された値考えられる。
この考え方をplotしてみると、
X1 <- c(1:200)
X2 <- c(1:200)
z<-matrix(0,nrow=200,ncol=200)
data1<-dnorm(X1,mean(x1),sd(x1))
data2<-dnorm(X2,mean(x2),sd(x2))
for(i in 1:200){
z[,i] <- data1[i]*data2
}
XX1<-matrix(0,nrow=200,ncol=200)
XX2<-matrix(0,nrow=200,ncol=200)
for(i in 1:200){
XX1[i,] <- c(1:200)
XX2[,i] <- c(1:200)
}
library(rgl)
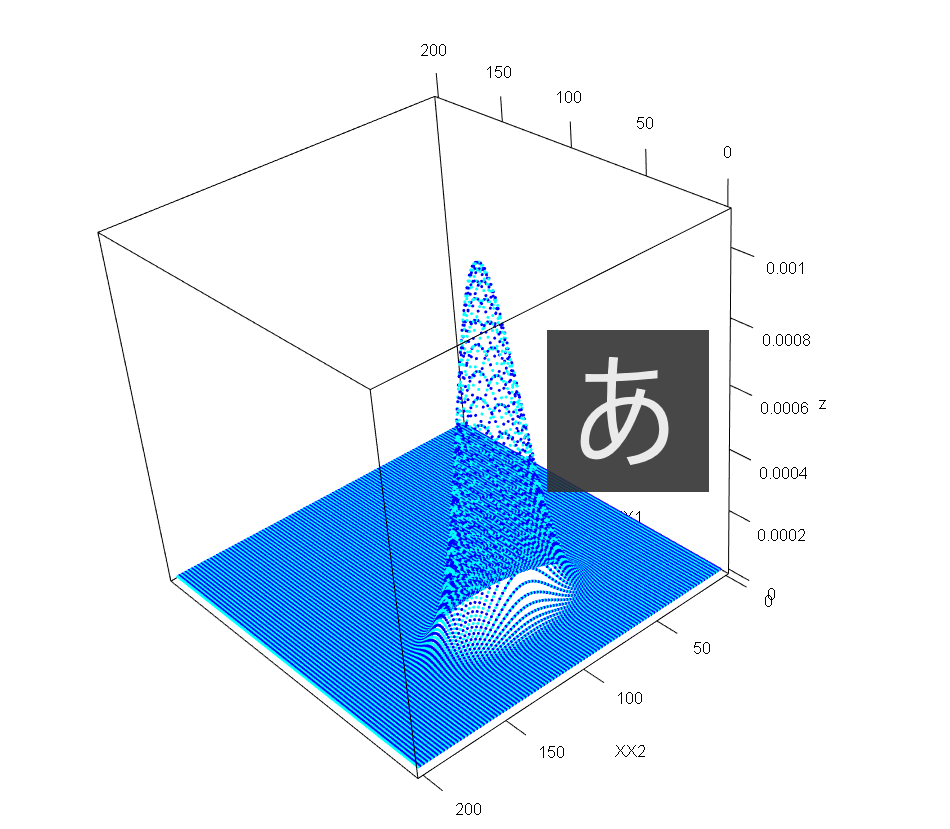
plot3d(XX1, XX2, z,col=c(4:5))
うまく表現できたとは言えないけども、二つの変数の平均は確率値が高くなっている。
中心から離れた値は0にべったり。
以上
ここに相関を考慮して分散行列とかが登場するとマハラノビスになるけどそれはまた今度。
rgl
ぐりぐり動かせてたのしい