コインの例を使って信頼区間を理解していきたいと思う。
60回のコインを投げる。
"正しいコイン"であれば理論的に30回表が出る
(正しいコインとは歪みや重さの偏りなどが無く、表も裏も0.5の確率で出現するコインの事)
60回コインを投げた時の分布は正規分布に近似することが知られている。
結果が成功失敗の二択である試行は、スイスの数学者ヤコブ・ベルヌーイの名をとってベルヌーイ試行と呼ばれる。
ベルヌーイ試行を独立にn回行った場合、
(1回投げる。また投げる。また投げる。これが独立。
独立でない=同時に何枚も投げることでコインがぶつかりあって理論的な確率がかわる)
その結果の分布は二項分布と呼ばれる。
編集2019 09 23
コメントより、コインがぶつかっても確率コインの持つ確率は変わらない。ぶつかったら表が出るコインなら別。
独立でないコインといえば、一度目が表なら二度目も表になる。といったように、
0.5の確率が影響を受けて変化するような時のこと。
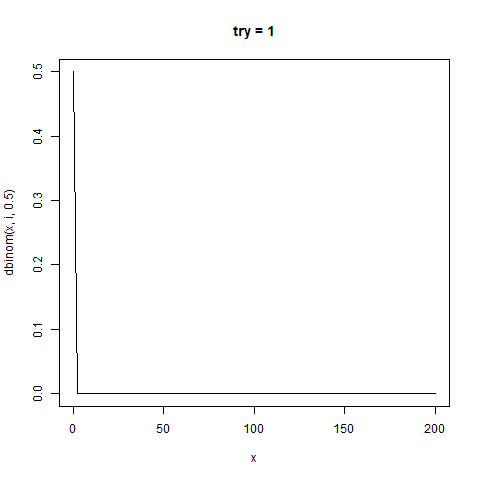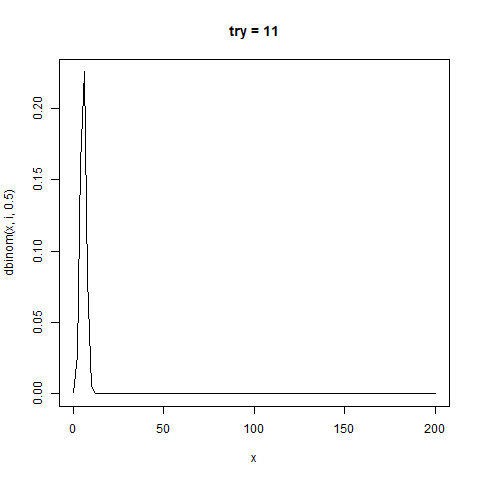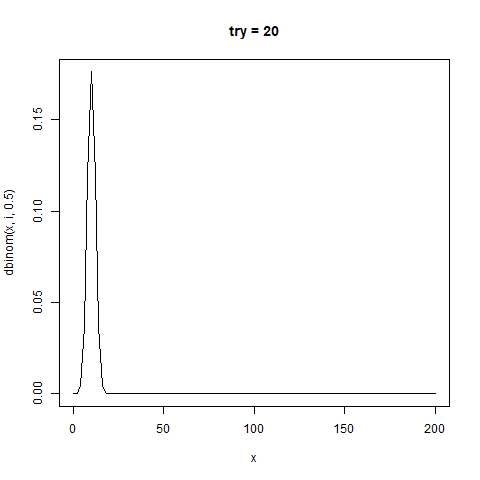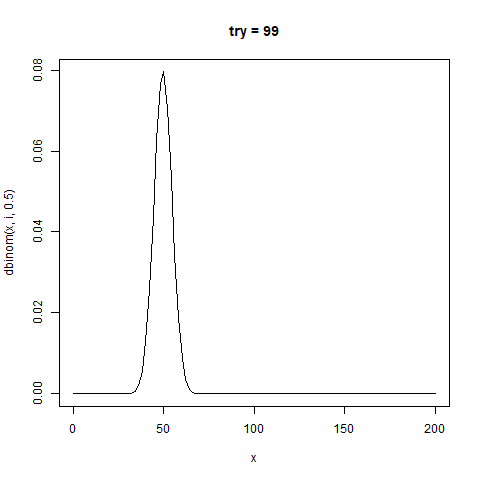
今回のように、試行回数n回で確率1/2の場合、
分布の中心(平均値)はn/2であり、標準偏差が√n/2の正規分布と近似することが知られている。
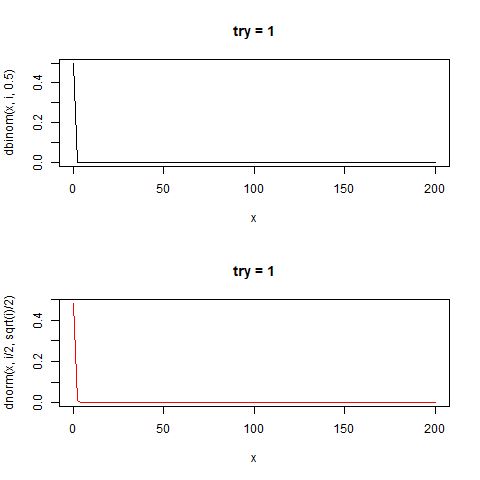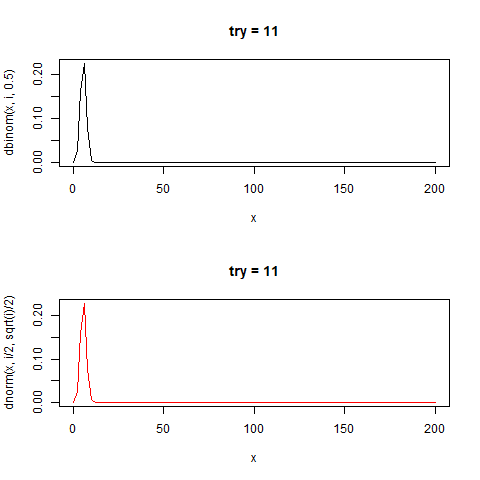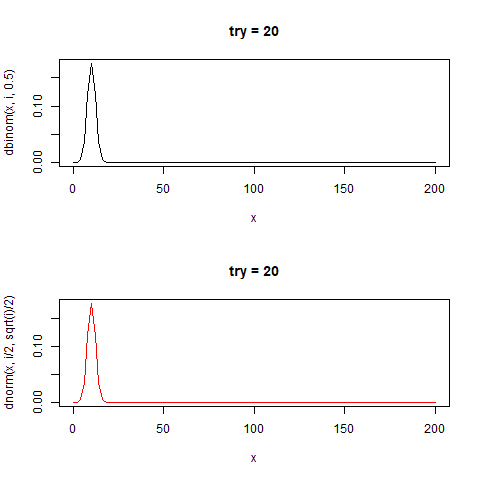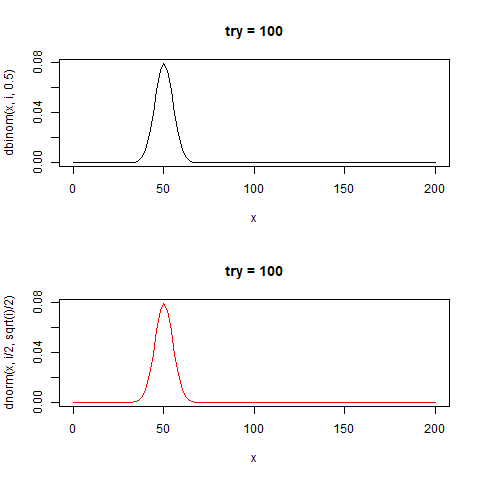
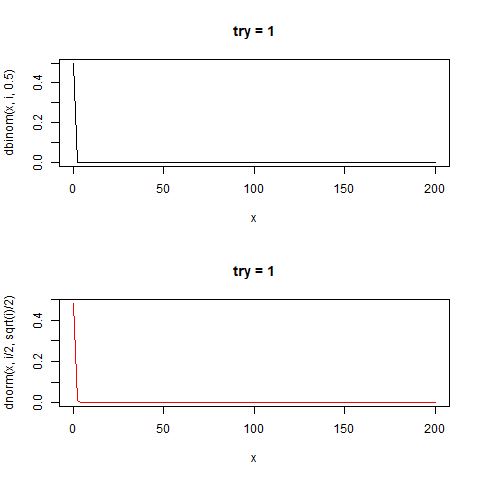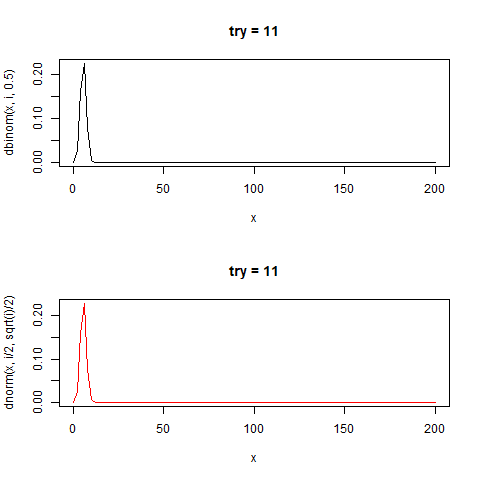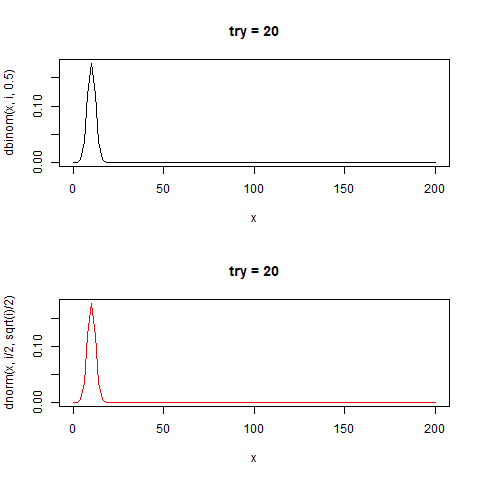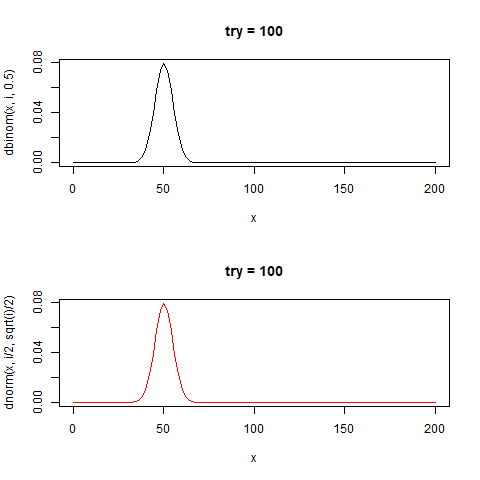
感覚がつかめなかったのでこれもgifにした
たしかに正規分布と似た形をしている。
使ったコードは以下
x <- seq(0,100,1)
for(i in 1:100){
#png(paste0(i,"_bi_reg.png"))
par(mfrow=c(2,1))
curve(dbinom(x,i,0.5),0,200,type="l",main=paste0("try = ",i))
curve(dnorm(x,i/2,sqrt(i)/2),0,200,type="l",col="red",main=paste0("try = ",i))
#dev.off()
}
検定時にはこの性質を利用して、zスコア(標準化得点)を求める。
今回は60回のコインを投げることを想定している。
60回のコインを投げた場合
平均は30回
標準偏差は
sqrt(60)/2 = 3.87
となる。
これが正規分布と近似する。
予言的中区間について
統計的に考えて、次に起こる現象を的中させたい。
というか的中は無理でも、高い確率で当てたい。
ピンポイントな指定で当てるのではなく、
この値からこの値までのを95%の確率で取るであろう。という予言をしたい。
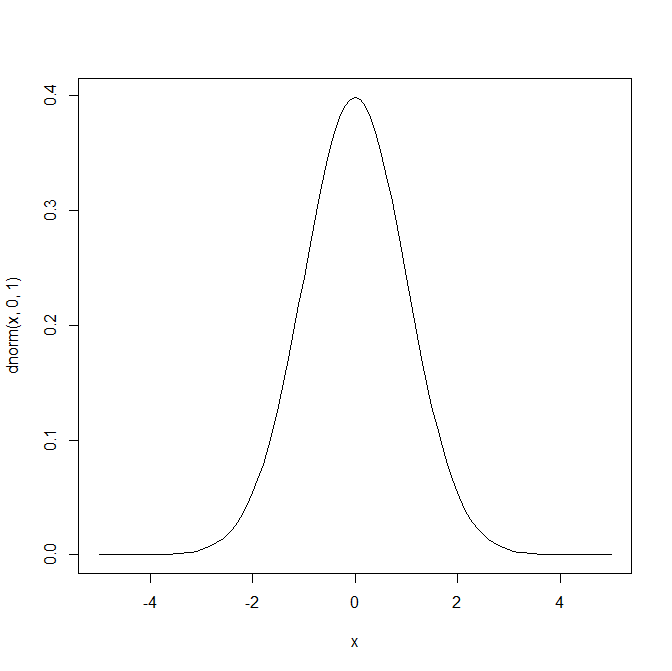
そのためには標準正規分布を使って考えよう。
標準正規分布は平均をゼロ、標準偏差を1にした正規分布のことである。
x <- seq(0,100,1)
curve(dnorm(x,0,1),-5,5,type="l",)
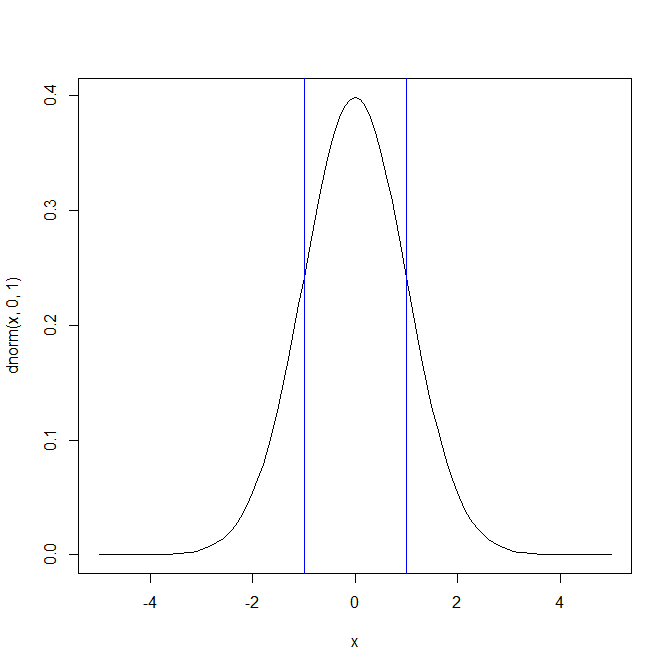
標準正規分布の中の面積を考える。
1σ区間の面積は、約67%である
x <- seq(0,100,1)
curve(dnorm(x,0,1),-5,5,type="l",)
abline(v=1,col="blue")
abline(v=-1,col="blue")
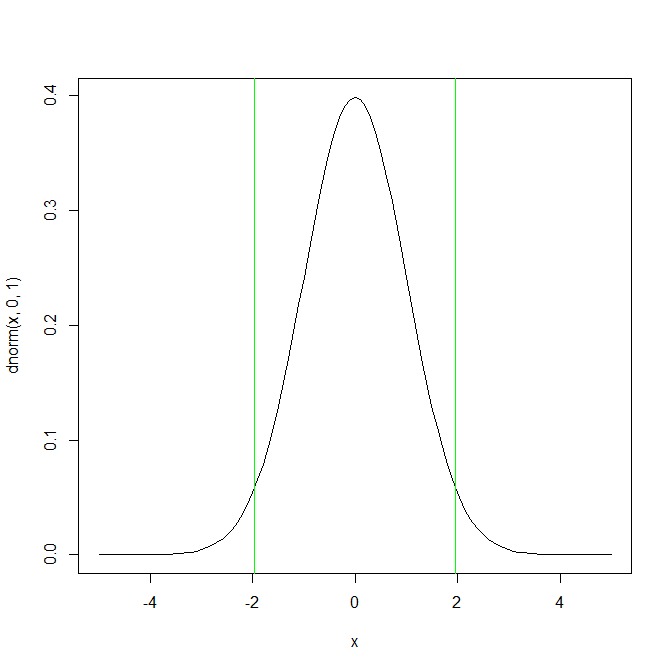
2σ区間(1.96)の区間では95%の面積を占める。
x <- seq(0,100,1)
curve(dnorm(x,0,1),-5,5,type="l",)
abline(v=1.96,col="green")
abline(v=-1.96,col="green")
確率密度関数の面積は、事象が起こる確率と考えることができるので、
次に起こる事象を95%の確率で予言したければ標準正規分布の±1.96の区間を考えればよい。
しかし、現在のコイン60回を投げる分布は
平均30回
標準偏差 3.87
であり、正規分布に近似はするが、標準正規分布ではない。
そこで標準正規分布に変形してやる。
標準化という手法でデータは標準正規分布に変形されることが知られている。
\frac{x-μ}{σ}
標準化とは、データxから平均μを引き、標準偏差で割る式である。
この計算をすることで、分布は標準正規分布に変形することができる。
実際に見てみよう。
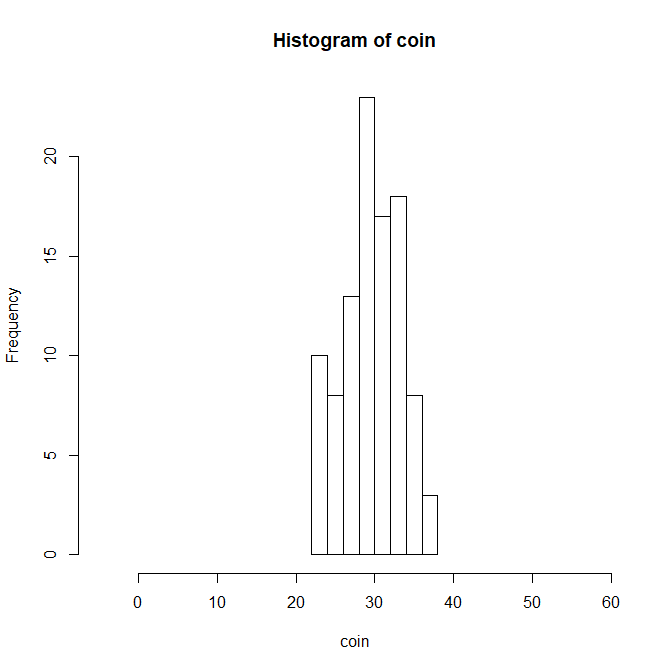
コイン60回を投げるという試行を100人に行ってもらったとする。
その結果は以下のようになる。
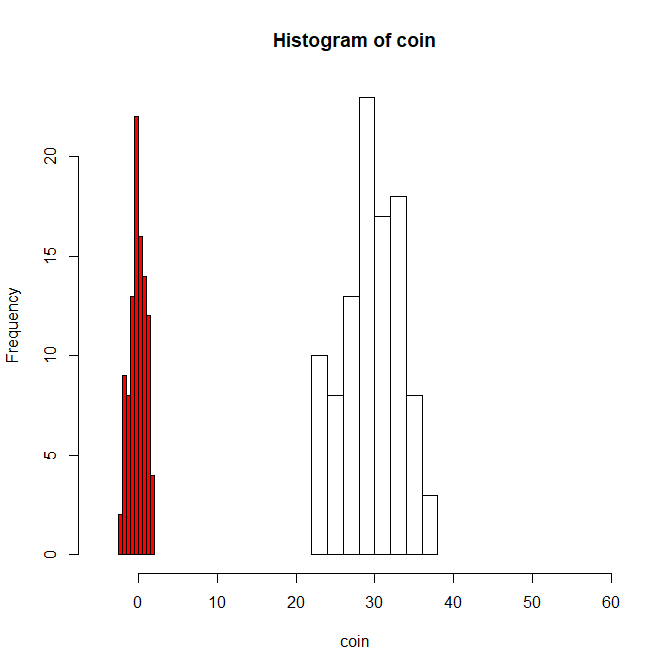
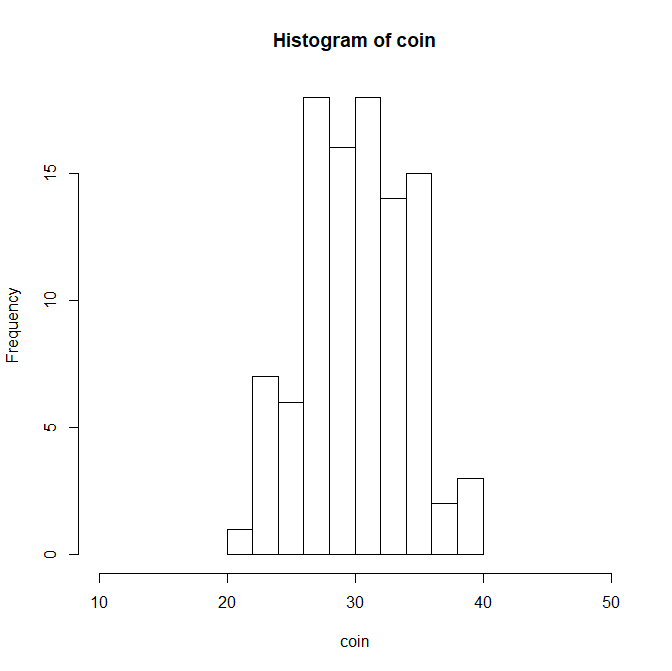
coin <- rnorm(100,30,3.8)
hist(coin,xlim=c(-5,60))
理論的な平均である30回付近を出した人数が最も多く、
理論的な平均から少しずれた人も見受けられる。
60回投げて20回~40回が表でした。
という結果は感覚的にも理解しやすいものであると思う。
このデータを標準化してみる。
normalization_coin <- (coin-30)/3.8
par(new=T)
hist(normalization_coin,xlim=c(-5,60),add=T,col="red")
平均が0で標準偏差が1になった。
標準偏差は間隔的に確認できないので、より詳細に確認してみる。
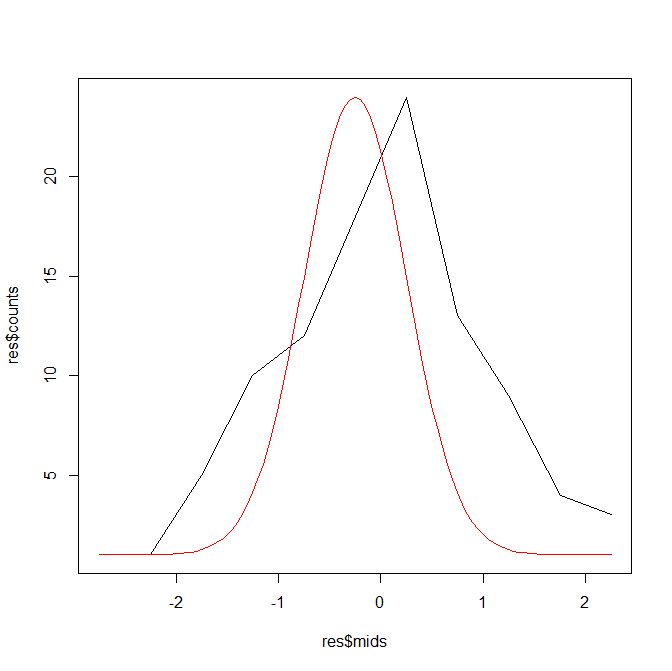
標準化したデータの分布に、平均0標準偏差1の分布を赤色で重ねている。
res <- hist(normalization_coin)
plot(res$mids,res$counts,type="l")
par(new=T)
curve(dnorm(x,0,1),-5,5,type="l",yaxt="n",xaxt="n",xlab="",ylab="",col="red")
なんとなく正しい気もするが、雑に重なっている気がする。
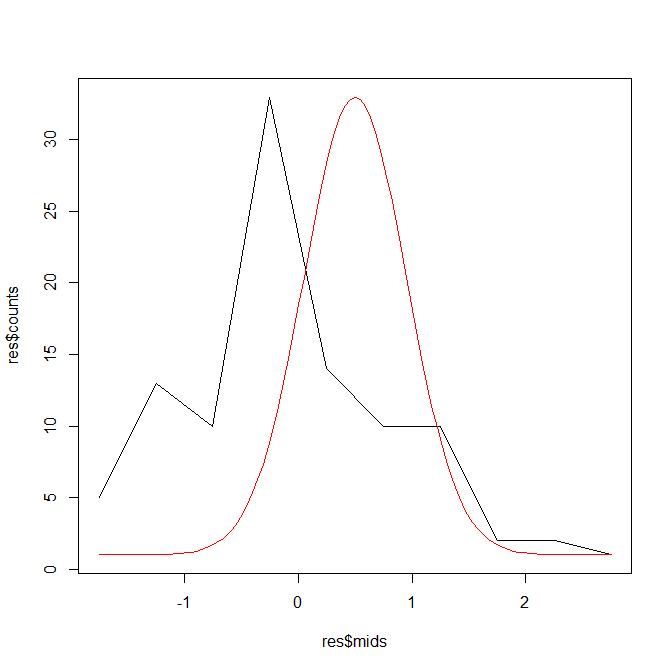
ひょっとしたら以下のような図になった人もいるのではないだろうか?
もっとひどい結果になる人もいると思う。
これは100人というサンプルサイズでは少なかったからである。
100人というサイズでは偶然発生するばらつきがカバーできず、正規分布とうまく重ならない。
たとえば100万人にやってもらったとしよう。
100万人もいれば偶然発生するばらつきは打ち消され、正規分布に近似するだろう。
coin <- rnorm(1000000,30,3.8)
hist(coin,xlim=c(-5,60))
normalization_coin <- (coin-30)/3.8
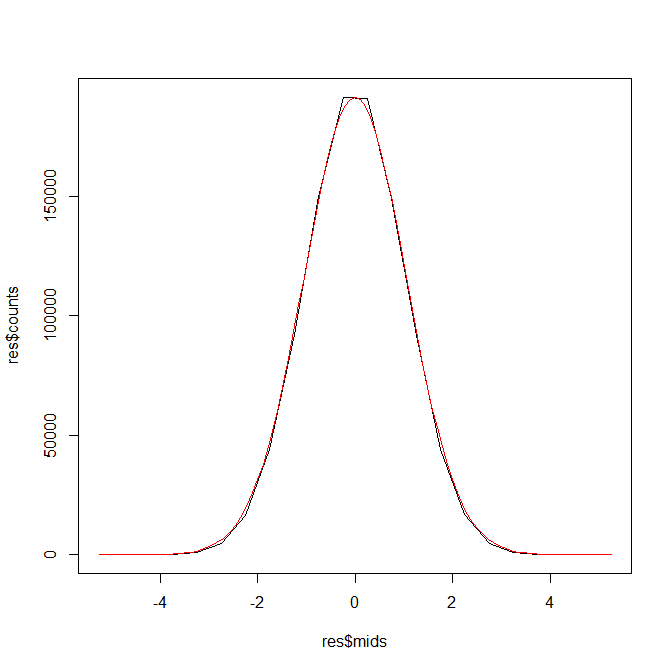
res <- hist(normalization_coin)
plot(res$mids,res$counts,type="l")
par(new=T)
curve(dnorm(x,0,1),-5,5,type="l",yaxt="n",xaxt="n",xlab="",ylab="",col="red")
ほぼ重なったのが確認できたと思う。
何度かこのスクリプトを繰り返せばほぼ完全に重なるときもある。
これは、100万人が60回のコイン投げを行ったとしても、少しくらいは平均30からズレてしまうということである。
これが極限定理の対数の法則である。
偶然ばらつきは、サンプルサイズを増やすことで打ち消し、本当の平均と本当の標準偏差に近づけることができる。という定理である。
ちなみに中心極限定理は母平均と標本平均の誤差の話であるので、混同しないように。
さて、標準化と標準正規分布に近似することを理解していただいたところで、
次は予言を的中させる方法について説明する。
つぎに観測する結果をxとおく。
標準化した値は標準正規分布に従い、
標準正規分布では±1.96の区間に95%のデータが存在するのであった。
つまり、
-1.96 < \frac{x-μ}{σ} < 1.96
-1.96 < \frac{x-30}{3.8} < 1.96
の区間を求めれば95%で起こる範囲を見つけられるということである。
実際に計算してみると、
-1.96*3.8 + 30 < x < 1.96*3.8 + 30
この計算を見ると、標準正規分布を平均30、標準偏差3.8に変形していることがわかる。
計算結果は
22.5 < x < 37.4
「あなたが60回コインを投げると、23~37枚が表である!」
と言っておけば95%は当たるのである。
100%当てたければ、表が出る範囲は0~60回である!と予言しておけば
100%当たる予言を言うことができる。
coin <- rnorm(100,30,3.8)
hist(coin,xlim=c(10,50))
ヒストグラムを見てもらったら、100人のうち22~37くらいの約95人が集まっていることが分かってもらえると思う。
coin <- rnorm(100,30,3.8)
res <- hist(coin,xlim=c(10,50))
df <- data.frame(number=res$counts,count=res$mids)
df2 <- df[df$count>22 & 37>df$count,]
print(paste("100人中",sum(df2$number),"人が22から37枚表"))
"100人中 94 人が22から37枚表"
95%信頼区間-母集団の母数(母平均)推定
この信頼区間と予言的中区間の区別がつかず、理解に苦労した。
コインでいくとわかりにくいので製造の話に置き換える
製造現場で鉛筆をつくっているとする
鉛筆の切り出しなど、生産時のばらつきが機械によってある。
この機械がつくる製品が、鉛筆の母集団にあたる。
機械の精度は±0.5cmまでは許容する設計である。
この精度±0.5 cmを標準偏差として置き換えたらいい。
感覚的に100本中68本はこの0.5の区間に入っているとすると、
0.5は95%区間である1σのばらつきと考えられる。
鉛筆の長さを10cmに設定しているとすると、
母集団は10 cm であるとすると。
母集団はμ = 10, σ = 0.5 である。
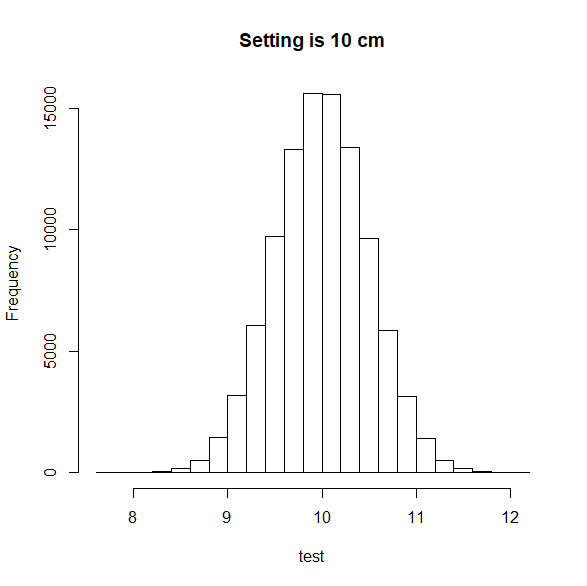
test<-rnorm(100000, 10, 0.5)
hist(test,main="Setting is 10 cm")
設計した条件から母集団は考えられた。
この機械を何十年と運用したあとにサンプルを1つ取ってきたとする。
この時採取したサンプルの値は10.5cmであった。(サンプル採取はカンペキに無作為である前提)
このサンプルの値 x を平均値として、xの周辺95%(1.96σ区間)を考えると、
その範囲に設定した母集団の平均があるはず!!
test<-rnorm(100000, 10, 0.5)
hist(test,main="Setting is 10 cm")
par(mfrow=c(2,1))
curve(dnorm(x,10,0.5),7,13,main="Setting is 10 cm",ylab="")
abline(v=10,col="red")
abline(v=0.5*2 + 10)
abline(v=-1*0.5*2 + 10)
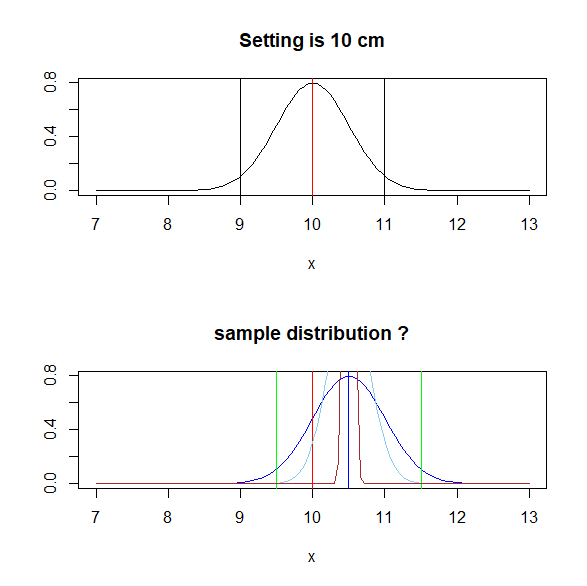
curve(dnorm(x,10.5,0.5),7,13,col="blue",ylab="",main="sample distribution ?")
abline(v=10.5,col="blue")
abline(v=0.5*2 + 10.5,col="green")
abline(v=-1*0.5*2 + 10.5,col="green")
abline(v=10,col="red")
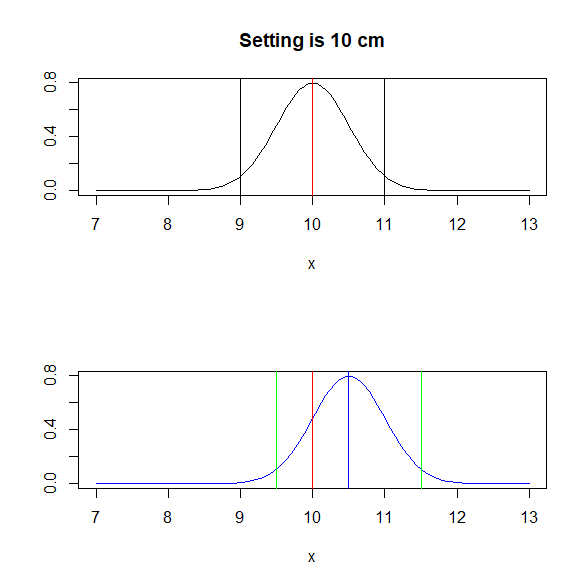
上図が母集団の分布と赤線が母集団平均である。
下図が抽出したサンプルの平均と、平均からの母平均でばらつきを考えた分布。
95%以内に母平均が含まれていることがわかる。
この範囲に母平均がなければ、
母集団の平均が全く変わってしまったか? (設計が狂っている)と考えられる。
サンプルサイズは多いほうがいい?
もちろん、偶然に外れたサンプルを取ってくることもあるだろう。
だから統計では「高い確率で異常"かもしれない"」という考え方で異常をみつけるのである。
サンプルの取り方はカンペキに無作為であった。
しかし1サンプルだけでは"偶然母平均から95%以上離れたサンプルだった"という確率も大いにあるだろう。
ならばサンプルサイズを増やせば良い
たとえば、母集団が100の集団から、サンプル数を10取ってきたとする。
95%以上離れた5つを"偶然"取ってきてしまっても、残りの95%以内の5つが誤差を緩和してくれる。
また、95%以上離れた5つが打ち消し合うかもしれない。
究極を言えば、母集団が100個なら標本を99個抽出したら、ほとんど母集団と差のない標本が作れるわけである。
こんな考えを聞くと、"サンプルサイズが多い方がいい"と巷で言われる理由も納得していただけるかとおもう。
しかし、次はこんな疑問が浮かぶだろう。
母集団を推定するときに、少ないサンプルサイズでは誤差の影響が強く出ることが分かった。
では全数100のうち、10のサインプルサイズで推定を行うときに、どのくらい誤差の影響が打ち消されたと言っていいのだろうか??
この疑問に対しては次の式が解決してくれる。
\frac{x-μ}{\frac{σ}{√n}}
母集団の標準偏差とは別に、サンプルサイズの標準偏差を考えてやる。
サンプルのデータから標準偏差を求めるのではなく、あくまでも母集団の標準偏差から得られたデータであることを考慮して、
母集団の標準偏差にサンプルサイズによる影響度を反映させたのである。
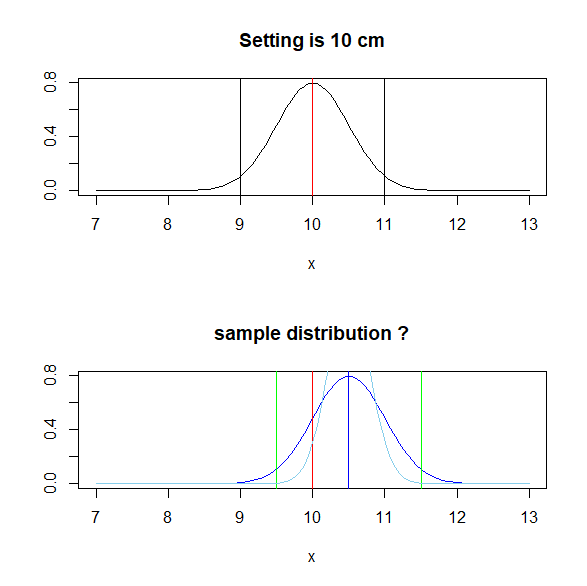
上記のサンプルの分布を水色の線に修正する。
サンプルが3個と少量だった場合にはどのように修正されるだろうか
curve(dnorm(x,10.5,0.5/sqrt(3)),7,13,col="sky blue",ylab="",main="sample distribution",add=T)
サンプルが少量だと、水色の範囲に母集団の平均があると推定される。
サンプルが増えると、分散は徐々に小さくなり、この範囲はより尖った狭い分布となっていく。
これはつまり、サンプルをたくさん取っても10.5という平均値が算出されるなら、
母集団の平均は、尖った狭い分布内にあるべきだ、ということになる。
curve(dnorm(x,10.5,0.5/sqrt(100)),7,13,col="brown",ylab="",main="sample distribution",add=T)
この事象を問題文に置き換えると以下のようになる。
問題・母集団平均の推定
ある工場で鉛筆の製品を無作為に3本抜し検査したところ、平均は10.5cmであった。
鉛筆の製品のばらつきは平均10,標準偏差0.5の正規分布に従うことが知られている。
この時、検査として抜き出した鉛筆から異常は考えられるだろうか?
H0 平均が10である
H1 平均が10ではない
zスコアは
Z= (10.5-10) / 0.5/√3
Z=0.577
となる。
10という平均よりも大きいので、正方向の1.96区間を考えると、
0.577は1.96よりも小さい。
よって平均は10であっても異常ではない。
という結果になる。
こんな質問もあるかもしれない。
ある工場で鉛筆の製品を無作為に3本抜し検査したところ、平均は10.5cmであった。
鉛筆の製品のばらつきは標準偏差0.5の正規分布に従うことが知られている。
この時、母平均が含まれる95%信頼区間を推定しろ。