前回と同じくInstant Gratificationに対してchris dotteさんがアプローチしている手法の開設を。
今回は、前回と同様に疑似ラベルを使いつつ、二次判別分析や多変量ガウス分布を考慮しながらモデルを作っていく。
内容がかなり難しかったので翻訳できている自身が"全く"ありません。
早速本編へ
二次判別分析 (Quadratic Discriminant Analysis, QDA) + 疑似ラベル + 混合正規? を使ったモデル化
このデータセットはsklearnのmake_classificationで作成されたと思われる512のデータのあつまりです。 EDAしてみたら、こんなパラメータで作成したのではないかと推測できました。
X, y = make_classification(n_samples=1024, n_features=255, n_informative=33+x,
n_redundant=0, n_repeated=0, n_classes=2, n_clusters_per_class=3,
weights=None, flip_y=0.05, class_sep=1.0, hypercube=True, shift=0.0,
scale=1.0, shuffle=True, random_state=None) # where 0<=x<=14
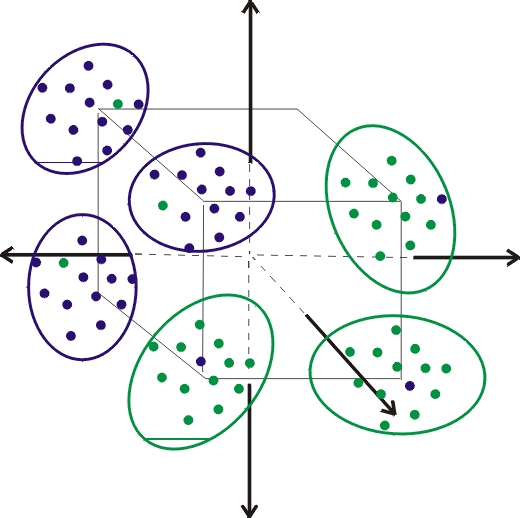
重要なパラメータはn_clusters_per_class=3 と n_informative=33+x です。 この意味は、データを六次元空間の超楕円体の33+xにすみわけさせたことである。
各超楕円は、multivariate Gaussian distributionなので、 クラス分けには、QDAと疑似ラベリングと混合正規分布を使った手法を選んだ。 (multivariate Gaussian distribution)は、多変量正規分布のこと。 平均と分散を持つ分布が例えば二次元で重なったとする。 そうすると、データには共分散が表れる。 多変量正規分布のなかでも多変量ガウス分布という表現をすると高次元のものを指していることが多い。
付録を見て。クラスごとに、3クラスタに分けているから。
ガウス過程回帰ってのは 正規分布から確率が一つ取り出せるけど、 ある時点の時にはあるパラメータを持った確率が取り出せて、 またある時には別のパラメータの確率分布が取り出せて、 というような考え方で、確率分布自体が抽出されていくようなもの。
なにが良いかというと、各時点で異なる分布を仮定してやって、それぞれの分布に重みをつけたら、 それらしい値が出てくるモデルが作れるのではないかって話。だと思う
完璧よりもさらに良き分類のために
もし、このコンペがmake_classificationでデータを作ったと仮定すると、 多くの参加者はGM(グラフィカルモデリング?)やQDAを使えばカンペキな分類ができるでしょう。 それゆえ、このコンペで勝つには、カンペキ以上の分類を行う必要があります。 このカーネルの分類器は、完璧なものよりも0.0005だけスコアを上げるランダム性を含んだモデル化をしています。
以下で説明。
もし、データがmake_classificationでつくられていたら、2.5%のランダムな要素以外を完全に予測できるでしょう。 この2.5%はどうしたって正しく予測はできないです。 ただし、予測モデルにもランダム性を加えてみたら、予測精度が少し上昇することがあります。 (時に悪化することもありますが。)
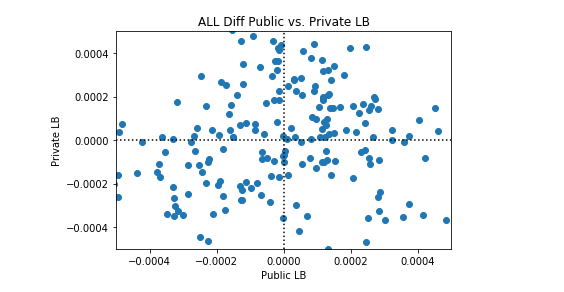
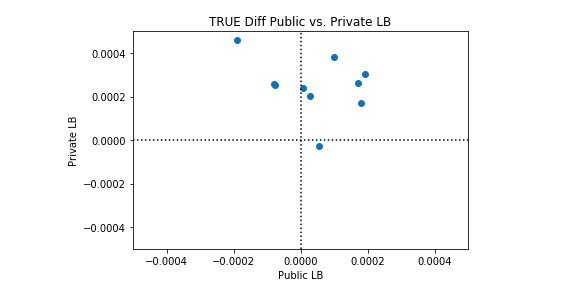
以下に示す図は精度を表しています。 点線はカンペキな分類器であり、各点はカーネルが、データセットに対して行った試みです。compのデータににている。 compってなに?????
200のどっとは10の試みによって作られた。20の異なるランダム性をもとに作成されたでーたセット。 黒の点線は完全に分類したときのAUCを出力するようにしたもの。詳細は付録3へ。
こんな感じです。
ほかには、平均で完璧に分類している?散布図は、相関を示していて、自分で確かめたスコアと投稿した時のスコアの関係である。
そんなこんなで、我々の最終的な成果物は、投稿時の最高スコアのものを使用している 30回くらいカーネルを走らせてみて、二つの成果物から選び、このスコアになった。
指を交差させ、二つのスコアが良く分類されるよう祈る。
import numpy as np
np.random.seed(42)
x = np.random.choice(np.arange(30),2)
print('We will submit versions',x[0],'and',x[1])
np.random.seed(None)
ちょっと追記
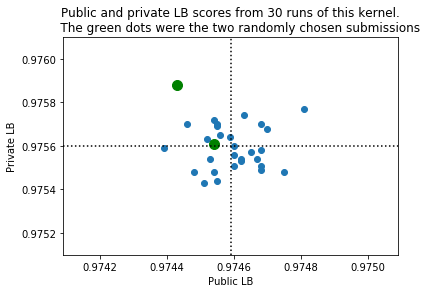
ラッキー! np.random.seed(42)を選んでよかった。コンペが終わった後、プライベートスコアと提出スコアの30個を比較した。 二つの緑の点は、ランダム性が6,19という値の時である。 19を見ると、プライベートスコアが良いのがわかるでしょう。 投稿したスコアの最高点は0.97481で、25個目の試行の時だった。 最も低いのは0.97439で、7回目の時だった。 プライベートスコアでは、19回目が最もよく、23回目が悪かった。 黒の点線は施行したスコアたちの平均値を表している。 詳細は付録3をみて。
import matplotlib.pyplot as plt, numpy as np
pu = np.array([68,53,70,67,54,54,39,68,60,65,46,62,62,55,54,
60,59,55,43,52,63,68,51,75,81,56,68,55,60,48])
pr = np.array([58,54,68,54,48,61,59,49,60,57,70,54,53,69,72,
56,64,44,88,63,74,70,43,48,77,65,51,70,51,48])
plt.scatter(0.974+pu/1e5,0.975+pr/1e5)
plt.scatter(0.974+pu[5]/1e5,0.975+pr[5]/1e5,color='green',s=100)
plt.scatter(0.974+pu[18]/1e5,0.975+pr[18]/1e5,color='green',s=100)
mpu = 0.974 + np.mean(pu)/1e5
mpr = 0.975 + np.mean(pr)/1e5
plt.plot([mpu,mpu],[mpr-0.0005,mpr+0.0005],':k')
plt.plot([mpu-0.0005,mpu+0.0005],[mpr,mpr],':k')
plt.xlabel('Public LB'); plt.xlim((mpu-0.0005,mpu+0.0005))
plt.ylabel('Private LB'); plt.ylim((mpr-0.0005,mpr+0.0005))
plt.title("Public and private LB scores from 30 runs of this kernel.\n \
The green dots were the two randomly chosen submissions")
plt.show()
ライブラリの読み込み
# IMPORT LIBRARIES
import numpy as np, pandas as pd, os
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import VarianceThreshold
from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
# LOAD TRAIN AND TEST
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')
df_train.head()
使えるデータの選別
使える特徴量をさがす。
分散の大きい特徴量がつかえる。
# IDENTIFY USEFUL FEATURES PER MAGIC SUB-DATASET
useful = np.zeros((256,512))
for i in range(512):
partial = df_train[ df_train['wheezy-copper-turtle-magic']==i ]
useful[:,i] = np.std(partial.iloc[:,1:-1], axis=0)
useful = useful > 1.5
useful = np.sum( useful, axis=0 )
カテゴリカルデータの0~512までの値でデータを取ってくる。 取ってきたデータの標準偏差を計算して、usefulに入れる
標準偏差が1.5以上であるものを残す。
512個の値にして、行の総和を計算。
モデルと予測
まず、QDAと疑似ラベルをtestに対して使ったところ、0.97の値が得られた。 疑似ラベルについてはひとつ前のカーネルを見て。 次に、三つの予測を作った(疑似ラベルで)、6楕円を見つけるために。 我々は3楕円が1を、ほかの3楕円が0を担当するようにsklearnの混合正規を使って分離しました。 0~5のラベルをそれぞれの楕円につけました。 最終的に、trainのQDAを6楕円を使って行い、予測しました。 ターゲットが1である、ということは、楕円3,4,5に当てはまるということ。というように。 付録2を見て。
確認として。 k-folds CVはつかってないです。 代わりに、合成データを生成し、最適化を適応させています。 そのほうがCVを改善させるんです。 モデルを作るとき1024行の予備データセットを使えます。 我々のモデルはmake_classのデータに対して、平均的に完璧な分類ができています。 しかし、多くの参加者もできるでしょう。
なのでランダム性を加えてよりよいものを生成するのです。
以下のコードは 合成データを作り、AUCを計算しています。 test.csvを予測してみましょう
# RUN LOCALLY AND VALIDATE
models = 512
RunLocally = True
# RUN SUBMITTED TO KAGGLE
if len(df_test)>512*300:
repeat = 1
models = 512 * repeat
RunLocally = False
# INITIALIZE
all_preds = np.zeros(len(df_test))
all_y_pu = np.array([])
all_y_pr = np.array([])
all_preds_pu = np.array([])
all_preds_pr = np.array([])
# MODEL AND PREDICT
for k in range(models):
# IF RUN LOCALLY AND VALIDATE
# THEN USE SYNTHETIC DATA
if RunLocally:
obs = 512
X, y = make_classification(n_samples=1024, n_features=useful[k%512],
n_informative=useful[k%512], n_redundant=0, n_repeated=0,
n_classes=2, n_clusters_per_class=3, weights=None, flip_y=0.05,
class_sep=1.0, hypercube=True, shift=0.0, scale=1.0, shuffle=True,
random_state=None)
# IF RUN SUBMITTED TO KAGGLE
# THEN USE REAL DATA
else:
df_train2 = df_train[df_train['wheezy-copper-turtle-magic']==k%512]
df_test2 = df_test[df_test['wheezy-copper-turtle-magic']==k%512]#数字%512をやると、512の時に0にもどる
sel = VarianceThreshold(1.5).fit(df_train2.iloc[:,1:-1])
df_train3 = sel.transform(df_train2.iloc[:,1:-1])
df_test3 = sel.transform(df_test2.iloc[:,1:]) #k=0のとき
#pd.DataFrame(df_train3)
#534 rows × 46 columns (使える変数)
obs = df_train3.shape[0]
X = np.concatenate((df_train3,df_test3),axis=0)#787*46 単純に結合させる関数っぽい
y = np.concatenate((df_train2['target'].values,np.zeros(len(df_test2))))#testにはtargetが入っていないので、ゼロを入れておく
# XとyはどちらもRunLocally = Trueのとき毎回値が変化する
# Faulsの時は値は変化しない
# TRAIN AND TEST DATA
train = X[:obs,:]
train_y = y[:obs]#534行
test = X[obs:,:]
test_y = y[obs:]#testの中の使える変数
comb = X #くっつけてcombという名前にする
# FIRST MODEL : QDA
# 二次判別分析でモデルを作っている
# 予測値をtest_predに入れている
clf = QuadraticDiscriminantAnalysis(priors = [0.5,0.5])
clf.fit(train,train_y)
test_pred = clf.predict_proba(test)[:,1]
# SECOND MODEL : PSEUDO LABEL + QDA
#0から1の間の乱数を発生させて、その値よりも大きい値をtest_predに入れる
#この状態はTFが入っている
#これが疑似ラベルだと思われる
#この状態のデータを使ってQDAを行う
test_pred = test_pred > np.random.uniform(0,1,len(test_pred))
clf = QuadraticDiscriminantAnalysis(priors = [0.5, 0.5])
clf.fit(comb, np.concatenate((train_y,test_pred)) )
test_pred = clf.predict_proba(test)[:,1]
# THIRD MODEL : PSEUDO LABEL + GAUSSIAN MIXTURE
#三つ目のモデルは疑似ラベルと混合ガウス
test_pred = test_pred > np.random.uniform(0,1,len(test_pred)) #またランダムで乱数を発生させて疑似ラベルとして
all_y = np.concatenate((train_y,test_pred))
#予測したyの値とtrainのyの値を結合させる
#TFのブール型は01のバイナリに変換される
least = 0; ct = 1; thx=150
while least<thx:
# STOPPING CRITERIA
if ct>=10: thx -= 10
else: thx = 150
# FIND CLUSTERS
clusters = np.zeros((len(comb),6))
# FIND THREE TARGET=1 CLUSTERS
train4 = comb[ all_y==1, :]
clf = GaussianMixture(n_components=3).fit(train4) #randomness
clusters[ all_y==1, 3:] = clf.predict_proba(train4)
# FIND THREE TARGET=0 CLUSTERS
train4 = comb[ all_y==0, :]
clf = GaussianMixture(n_components=3).fit(train4) #randomness
clusters[ all_y==0, :3] = clf.predict_proba(train4)
# ADJUST CLUSTERS (EXPLAINED IN KERNEL COMMENTS)
for j in range(5): clusters[:,j+1] += clusters[:,j]
rand = np.random.uniform(0,1,clusters.shape[0])
for j in range(6): clusters[:,j] = clusters[:,j]>rand #randomness
clusters2 = 6 - np.sum(clusters,axis=1)
# IF IMBALANCED TRY AGAIN
least = pd.Series(clusters2).value_counts().min(); ct += 1
# FOURTH MODEL : GAUSSIAN MIXTURE + QDA
clf = QuadraticDiscriminantAnalysis(priors = [0.167, 0.167, 0.167, 0.167, 0.167, 0.167])
clf.fit(comb,clusters2)
pds = clf.predict_proba(test)
test_pred = pds[:,3]+pds[:,4]+pds[:,5]
# IF RUN LOCALLY, STORE TARGETS AND PREDS
if RunLocally:
all_y_pu = np.append(all_y_pu, test_y[:256])
all_y_pr = np.append(all_y_pr, test_y[256:])
all_preds_pu = np.append(all_preds_pu, test_pred[:256])
all_preds_pr = np.append(all_preds_pr, test_pred[256:])
# IF RUN SUBMIT TO KAGGLE, PREDICT TEST.CSV
else:
all_preds[df_test2.index] += test_pred / repeat
# PRINT PROGRESS
if ((k+1)%64==0)|(k==0): print('modeled and predicted',k+1,'magic sub datasets')
# IF RUN LOCALLY, COMPUTE AND PRINT VALIDATION AUCS
if RunLocally:
all_y_pu_pr = np.concatenate((all_y_pu,all_y_pr))
all_preds_pu_pr = np.concatenate((all_preds_pu,all_preds_pr))
auc1 = roc_auc_score(all_y_pu_pr, all_preds_pu_pr)
auc2 = roc_auc_score(all_y_pu, all_preds_pu)
auc3 = roc_auc_score(all_y_pr, all_preds_pr)
print('Validation AUC =',np.round(auc1,5))
print('Approx Public LB =',np.round(auc2,5))
print('Approx Private LB =',np.round(auc3,5))
modeled and predicted 1 magic sub datasets
modeled and predicted 64 magic sub datasets
modeled and predicted 128 magic sub datasets
modeled and predicted 192 magic sub datasets
modeled and predicted 256 magic sub datasets
modeled and predicted 320 magic sub datasets
modeled and predicted 384 magic sub datasets
modeled and predicted 448 magic sub datasets
modeled and predicted 512 magic sub datasets
Validation AUC = 0.97538
Approx Public LB = 0.97543
Approx Private LB = 0.97533
aucをprintして
最後にsubmit
sub = pd.read_csv('../input/sample_submission.csv')
sub['target'] = all_preds
sub.to_csv('submission.csv',index=False)
plt.hist( test_pred ,bins=100)
plt.title('Model 512 test predictions')
plt.show()
# 予測結果をplotすると図のようになる
whileあたりからわけわからん!
least = 0; ct = 1; thx=150
#こんなパラメータを用意して
while least<thx:
# STOPPING CRITERIA
#もしもleastがthxよりも小さかった時で、
if ct>=10: thx -= 10
#さらにもしもctが10よりも大きければ、thxにはthx-10を入力する
else: thx = 150
#もしもctがこの条件に当てはまらなければthxには150を入れる
# FIND CLUSTERS
clusters = np.zeros((len(comb),6))
#クラスタという名前の変数にはcombと同じ長さの0を6つ作る
# FIND THREE TARGET=1 CLUSTERS
train4 = comb[ all_y==1, :] #1の時の値を入れて
clf = GaussianMixture(n_components=3).fit(train4) #randomness
#ガウシアンミクスチャーでtrain4についてのモデルを作って
clusters[ all_y==1, 3:] = clf.predict_proba(train4)
#train4にモデルを適応させてやったものを
#clustersの中の0が6個入っているものの、後半3つに予測値を代入していく
# FIND THREE TARGET=0 CLUSTERS
train4 = comb[ all_y==0, :]
clf = GaussianMixture(n_components=3).fit(train4) #randomness
clusters[ all_y==0, :3] = clf.predict_proba(train4)
#こっちは前半3つに入れている
# ADJUST CLUSTERS (EXPLAINED IN KERNEL COMMENTS)
for j in range(5): clusters[:,j+1] += clusters[:,j]#クラスタの(787, 6)のうち、すべての列の隣の列に、左の列を足したものを代入していく
rand = np.random.uniform(0,1,clusters.shape[0])#クラスタの次元に合うだけの乱数を発生させる
for j in range(6): clusters[:,j] = clusters[:,j]>rand #randomness
#クラスタの中の値でrandよりも大きいものを代入する
clusters2 = 6 - np.sum(clusters,axis=1)
#clustersには合計値を入れているので、6を引いてやる
#すると0~5の6個のクラスタに分けられる
# IF IMBALANCED TRY AGAIN
least = pd.Series(clusters2).value_counts().min(); ct += 1
#6クラスに分けたが、少なくとも120個のデータは各クラスが持っているようにするまで繰り替えす
# FOURTH MODEL : GAUSSIAN MIXTURE + QDA
clf = QuadraticDiscriminantAnalysis(priors = [0.167, 0.167, 0.167, 0.167, 0.167, 0.167])
#QDAの判別は0.167を入れている。合計するとほぼ1
clf.fit(comb,clusters2)
#クラスタ2で何番目の楕円に含まれているか定義してあるので適応させてる
pds = clf.predict_proba(test)
#testに対してモデルを使って予測している
test_pred = pds[:,3]+pds[:,4]+pds[:,5]
#pdsの後半3つを足してる。後半3つといえばclustersにはtarget=1の時の値だったと思う
#クラスタ分けしておいて、その確率を足し合わせて1,0を判断させる仕組みか?
# IF RUN LOCALLY, STORE TARGETS AND PREDS
if RunLocally:
all_y_pu = np.append(all_y_pu, test_y[:256])#trainの列かな?
all_y_pr = np.append(all_y_pr, test_y[256:])#testの列かな?
all_preds_pu = np.append(all_preds_pu, test_pred[:256])
all_preds_pr = np.append(all_preds_pr, test_pred[256:])
# IF RUN SUBMIT TO KAGGLE, PREDICT TEST.CSV
else:
all_preds[df_test2.index] += test_pred / repeat
# PRINT PROGRESS
if ((k+1)%64==0)|(k==0): print('modeled and predicted',k+1,'magic sub datasets')
# 64回目ごとに表示させていく。合計9回表示されることになる
これで予測スコア0.975という高い値が出ました。
内容もよく分からないので付録解説やコメントを読んでいきます。
いや、超立方体とか出てきてホント分からないのでわかるようになってから出直すと思います。
付録1
今回のデータはsklearnのmake_classificationで作られたと考えています。
ここで重要なのは、kaggleが「n_clusters_per_class」をいくつで設定してデータを作ったのか?ということです。
これは、長さ「2 * class_sep」の辺を持つn次元のハイパーキューブの頂点について正規分布(std = 1)されたポイントのクラスターを最初に
作成し、各クラスに同数のクラスターを割り当てます。
つまり、3つの次元では、クラスターはこれらの8つの場所のいずれかに集中します。
(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)
1をすべて「class_sep」に置き換えます。
1024行のデータを作成し、1クラスごとに2つのクラスターを持ちます。
target = 1の場合、(-1、1、-1)を中心とする256ポイントと(1、1、-1)を中心とする256ポイントの2つの集団があります。
target=0の時、256ポイントが(1、1、1)を中心に、256ポイントが(-1、-1、1)を中心とする集団があります。
EDAを使用して、実データのクラスとクラスター数を決定していきます。
Sklearnのmake_classificationは、ハイパーキューブの角でデータ(楕円)を生成します。
したがって、n_clusters_per_class = 1のみが存在する場合、データの各楕円(target = 1およびtarget = 0)の中心には、すべての座標1と-1が含まれます。たとえば、(1,1、-1,1、-1、-1,1 、...)。
したがって、すべての変数の平均(中心座標)のヒストグラムをプロットすると、1と-1にbumpが見られます。
(変数によって各サブデータセット内を意味します。これは768行のtrainとtestです。元のtrainの列の262144行すべてを意味するわけではありません)。←ここは262144を256変数で割ると1024になる。
n_clusters_per_class = 2の場合、1つのサブデータセット内で、target = 1に2つの楕円ができます。
たとえば、(-1,1、...)を中心とする1つの楕円と(1,1、...)を中心とする楕円があり、変数の計算時に1と-1の最初の座標は平均0になります。
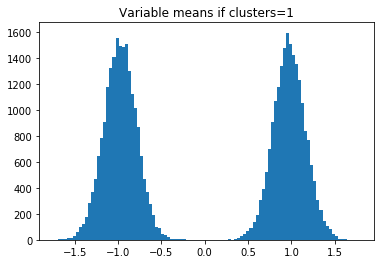
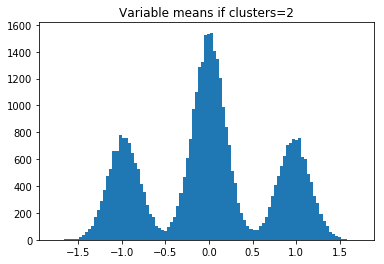
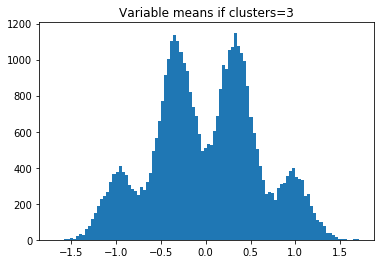
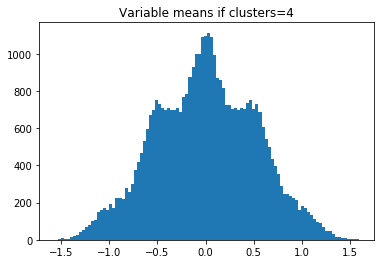
したがって、clusters = 2の場合、-1、0、および1でヒストグラムバンプが表示されます。n_clusters_per_class= 3の場合、4つのバンプが表示されます。
これは合成データで確認できます。 wheezy-magicサブデータセットごとに768行しかない比較対象のトレーニングデータと公開テストデータしかないため、n_samples = 768を使用します。
その後、実データの変数平均(サブデータセット内)のヒストグラムをプロットし、どのn_clusters_per_classが一致するかを確認します。 または、モデルを構築し、n_clusters_per_classが1、2、3、または4に等しいと仮定することができます。次に、どのn_clusters_per_classが最大のCVを持つかを確認します。 これらのメソッドは両方とも、n_clusters_per_class = 3であると判断します。
for clusters in range(4):
centers = np.array([])
for k in range(512):
X, y = make_classification(n_samples=768, n_features=useful[k],
n_informative=useful[k], n_redundant=0, n_repeated=0,
n_classes=2, n_clusters_per_class=clusters+1, weights=None,
flip_y=0.05, class_sep=1.0, hypercube=True, shift=0.0, scale=1.0,
shuffle=True, random_state=None)
centers = np.append(centers,np.mean(X[ np.argwhere(y==0).flatten() ,:],axis=0))
centers = np.append(centers,np.mean(X[ np.argwhere(y==1).flatten() ,:],axis=0))
plt.hist(centers,bins=100)
plt.title('Variable means if clusters='+str(clusters+1))
plt.show()
実際のデータをplotしてみる
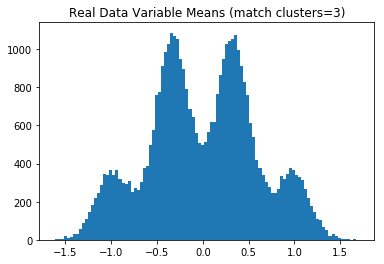
まず、QDAを使用してtestデータの擬似ラベルを作成します。
次に、すべてのトレーニングおよび擬似ラベル付きtestデータを組み合わせて(サブデータセットごとに768行)使用して、target = 0およびtarget = 1の変数平均(データセンターの座標)のヒストグラムをプロットします。 以下のプロットは、Kaggleがn_clusters_per_class = 3を使用したことを示しています。
centers = np.array([])
for k in range(512):
# REAL DATA
df_train2 = df_train[df_train['wheezy-copper-turtle-magic']==k]
df_test2 = df_test[df_test['wheezy-copper-turtle-magic']==k]
sel = VarianceThreshold(1.5).fit(df_train2.iloc[:,1:-1])
df_train3 = sel.transform(df_train2.iloc[:,1:-1])
df_test3 = sel.transform(df_test2.iloc[:,1:])
obs = df_train3.shape[0]
X = np.concatenate((df_train3,df_test3),axis=0)
y = np.concatenate((df_train2['target'].values,np.zeros(len(df_test2))))
# TRAIN AND TEST DATA
train = X[:obs,:]
train_y = y[:obs]
test = X[obs:,:]
test_y = y[obs:]
comb = X
# FIRST MODEL : QDA
clf = QuadraticDiscriminantAnalysis(priors = [0.5,0.5])
clf.fit(train,train_y)
test_pred = clf.predict_proba(test)[:,1]
# SECOND MODEL : PSEUDO LABEL + QDA
test_pred = test_pred > np.random.uniform(0,1,len(test_pred))
clf = QuadraticDiscriminantAnalysis(priors = [0.5, 0.5])
clf.fit(comb, np.concatenate((train_y,test_pred)) )
test_pred = clf.predict_proba(test)[:,1]
# PSEUDO LABEL TEST DATA
test_pred = test_pred > np.random.uniform(0,1,len(test_pred))
y[obs:] = test_pred
# COLLECT CENTER COORDINATES
centers = np.append(centers,np.mean(X[ np.argwhere(y==0).flatten() ,:],axis=0))
centers = np.append(centers,np.mean(X[ np.argwhere(y==1).flatten() ,:],axis=0))
# PLOT CENTER COORDINATES
plt.hist(centers,bins=100)
plt.title('Real Data Variable Means (match clusters=3)')
plt.show()
付録2
上記のコードでmake_classificationで完全に分類できていた。
さらに改善させるためのアイディアを書いていきます。
案1
4分類器?4つ目の分類器?を作成しtrainを分類させることが出来ます。
その場合、abs(oof-true)> 0.9のすべてのトレーニングデータは、ラベルがフリップされた誤ったトレーニングデータです。次に、これらのトレーニングラベルを修正し、カーネル全体をもう一度実行します。
案2
各クラスターの中心はハイパーキューブコーナーであるため、meang [np.argwhere(meang> = 0)] = 1.0およびmeang [np.argwhere(meang <0)] = -1.0を追加することにより、Sklearnの2次判別分析コードを変更できます。これにより、すべてのクラスターの中心がハイパーキューブコーナーに移動します。
案3
コンピューターの精度では、1に近い予測を区別できません。6桁の精度の例を使用すると、1.000001と1.000002の数値は両方とも1.00000になるため同じです。 AUCを改善するために、このカーネルに次のコードを追加できます。 temp = np.log(pds [:、0] + pds [:、1] + pds [:、2]); temp [np.isinf(temp)] = -1e6; test_pred-= temp。これにより、1に近い予測を区別することでAUCが改善されます。0.0000001と0.0000002の数値は1.0e-7と2.0e-7であり、コンピューターはすでにそれらを区別できるため、0に近い予測の問題ではないことに注意してください。
案4
test.csvの予測を行った後、それらを擬似ラベルとして使用し、カーネル全体を2回実行できます。次に、これらのラベルを使用して、カーネルを3回実行します。反復ごとにわずかに増加する可能性があります。
案5
このカーネルを複数回実行して、平均を取ることができます。または、kフォールドを使用します。これにより、このコードの分散(ランダム性)が除去され、毎回プリフェクションに近い結果が得られますが、LB 0.00050が完璧よりも多かれ少なかれ得点される可能性もなくなります。
案6
また、二次判別分析と混合ガウスのSklearnのコードを変更することにより、このコードの分散(ランダム性)を削除できます。これらの各モデルは、0または1のトレーニングラベルのみを受け入れます。数行のコードを追加することにより、これらのモデルが連続確率を受け入れ、重みとして使用できるようになります。これにより、ランダム化ラインtest_pred = test_pred> np.random.uniform(0,1、len(test_pred))を削除できます。代わりに、0〜1の確率として擬似ラベルを残し、QuadraticDiscriminantAnalysis.fit(test_data、test_pred)を呼び出すことができます。
これらの追加の高度な手法を組み合わせて使用することで、このカーネルはこのコンペティションの公開リーダーボードでLB 0.97489を獲得することができました。しかし、検証により、これらの手法は基本的な完全な分類器をそれ以上完璧にしないことが示されました。したがって、最終提出には、基本分類子が使用されました。
付録3
モデルを合成データに適用することにより、シミュレートされたパブリックリーダーボードとプライベートリーダーボードでどのように機能するかを学習できます。 このカーネルが平均して完全性を達成することを確認します(Kaggleが疑わしいパラメーターでmake_classificationを使用した場合)。 make_classificationのSklearnのコードには以下が含まれます
# Randomly replace labels
if flip_y >= 0.0:
flip_mask = generator.rand(n_samples) < flip_y
y[flip_mask] = generator.randint(n_classes, size=flip_mask.sum())
変数yが書き換えられる前に、y_orig = y.copy()を追加して保存できます。 次に、シャッフル行をX、y、y_orig = util_shuffle(X、y、y_orig、random_state = generator)に更新します。 次に、make_classificationの最後の行を変更して、X、y、y_origを返します。 これを行うことにより、prefect = roc_auc_score(y、y_orig)を使用して完全な分類器のAUCを計算できます。
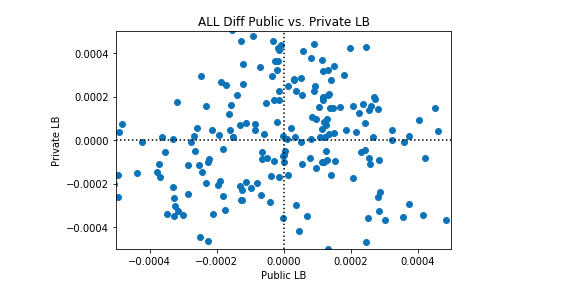
これで、このコンペティションのデータに類似した数百の合成データセットを作成し、このカーネルを適用して、完璧な分類器と比較してどれだけうまく機能するかを確認できます。合成データセットごとに、このカーネルを10回実行します。これはパターンを示し、2つの最終提出物の選択方法を決定するのに役立ちます。
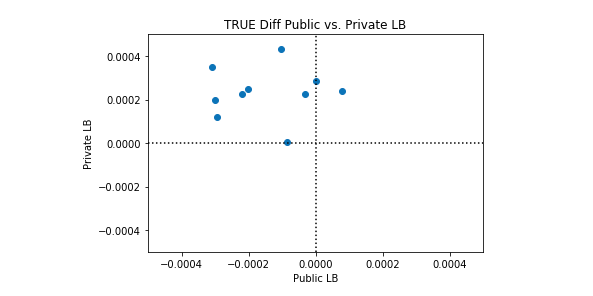
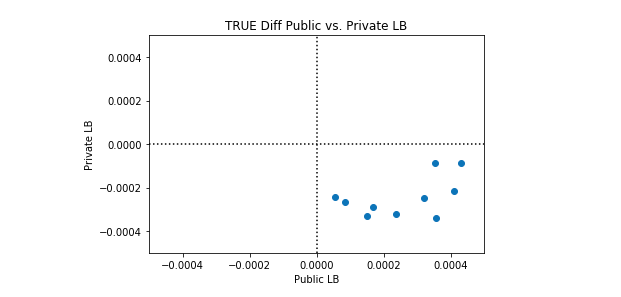
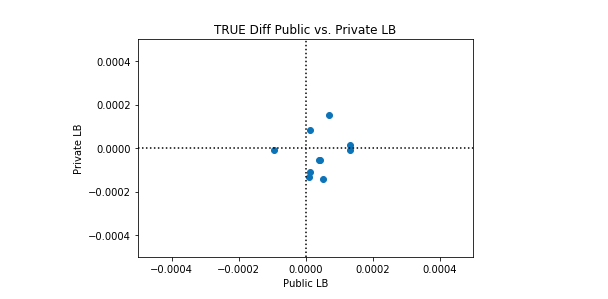
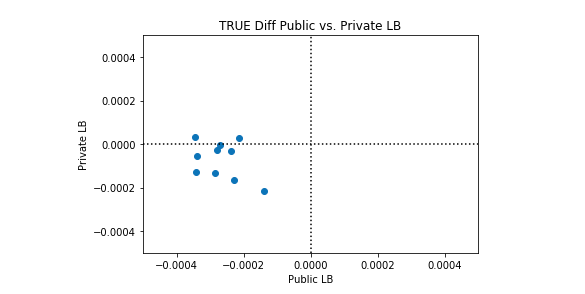
私たちは、このケネルが完璧よりも優れている場合と、完璧よりも悪い場合があることを観察します。興味深いのは、パブリックLBとプライベートLBのパフォーマンスに相関関係がないことです。以下のプロット例では、完全な分類は黒い点線で表されています。
多くのシンセティックデータセットでこのカーネルのパフォーマンスの平均を取ると、完全な分類が達成されます。したがって、このカーネルを改善する理由はありません。平均的な完璧な分類よりも優れたパフォーマンスを期待することはできません。考慮できる唯一の変更は、このカーネルの完全性からの標準偏差を変更することです。カーネルを実行するたびに完全性を達成しようとするか、(そのままにして)いくつかのカーネル実行で所望の量だけ完全性をランダムに超えることを試みることができます。
Synthetic Dataset 1
Synthetic Dataset 2
Synthetic Dataset 3
Synthetic Dataset 4
Synthetic Dataset 5
Many Synthetic Datasets Together
わからんったらわからん!
コメント
Q:なんで疑似ラベル作るときのランダム性を
test_pred = test_pred > np.random.uniform(0,1,len(test_pred))
で判別してるの?
前回投稿してたカーネルでは
( >0.99 or <0.01 )
で判別してなかった?
A:
262144のテスト(パブリックとプライベート)の観測があります。 0.99以上0.01以下を使用すると、85%の疑似ラベルのみを使用します。 しかし、私はそれらのすべてをGMM用にしたいです。
問題は、テストの観測値に0.65の予測がある場合、0または1の擬似ラベルを付ける必要がありますか? 確率で決めます。 まず、r = np.random.uniform(0,1)を呼び出します。 0.6> rの場合、テスト観測1に疑似ラベルを付けます。0.6<rの場合、テスト観測0に疑似ラベルを付けます。
その後、すべての262144テスト観測に疑似ラベルを付けます。
さらに続けてQ:しかし、ランダムに "RANDOM.uniform"で確率を生成すると(テスト観測の予測値は0.65であり、確率は0になる場合があります。56(擬似ラベルはTRUE)、次回は確率が0.99(擬似ラベルFALSE)になります。 ランダムに生成された確率がデータ全体に影響を与えるかどうかはわかりません。)
私は次のコードを数回実行します(512個のモデルの1つ)、合計がちょうど数の周りにあることがわかります(合計の差はランダムな確率によって作成されました。)
np.sum(testpred> np.random.uniform(0,1、len(testpred))))
申し訳ありませんが、私の英語は苦手です。
詳しく説明してもらえますか?
確率をランダムに生成すると、Pseudoラベルにランダム性が追加される可能性があると思います。ランダム性は、プライベートデータでモデルをより良くすることができますか?
それが正しいかどうかはわかりません。
A:はい、正確に。 ランダム性を追加することにより、カーネルは、プライベートLB 0.97588をスコアリングすることで達成した、完全なプライベートLB 0.97579よりも優れたパフォーマンスを実現する可能性があります。 (完全な分類はここで説明されています)。
https://www.kaggle.com/c/instant-gratification/discussion/97047
Q:ラベルを平滑化する理由は何ですか?
A:predict_proba()の代わりにpredict()を使用して、コードを6行短縮できました。 たとえば、clusters2 [all_y == 0、:3] = clf.predict(train4)を使用して、ラベルを「平滑化」または「調整」とラベル付けしたセクション全体を削除します。
クラスごとに2つのクラスターしかないことを考慮してください。 クラスター0とクラスター1は、ターゲット= 0用であるとします。 次に、Pr(cluster = 0)<0.5のすべてのポイントはクラスター0とラベル付けされます。Pr(cluster = 0)> = 0.5のすべてのポイントはクラスター1とラベル付けされます。Pr(cluster = 0)= 0.25の場合、クラスター1に入る確率は0.25です。
したがって、ラベルを「スムージング」または「調整」する目的は、すべてのポイントにクラスター0または1のいずれかになる機会を与えることです。各ポイントに対して、0〜1の乱数を選択します。Pr(cluster = 0 )>乱数の場合、ラベルはクラスター1です。それ以外の場合、ラベルはクラスター0です。
Q:クラスごとのnクラスターの推定に関して:3Dの例を取り上げて、クラスごとに3つのクラスターがあると仮定します。 target = 1のクラスターの中心が(1,1,1)、(-1、-1、-1)、(1,1、-1)にあると想像してください。 その場合、変数を計算すると、1/3と-1/3でのみバンプが表示されます。 そこで、クラスごとの正しいnクラスターがclass_sep = 1/3で2ではなく3であることをどのように識別しますか?
A:3Dとサブデータセットが1つしかない場合は難しいでしょう。 変数の平均が3つしかないため、4つの値(-1、-1 / 3、1 / 3、1)を持つことはできません。 幸いなことに、40のディメンションと512のサブデータセット(20480の可変平均)があるため、-1、-1 / 3、1 / 3、および1にバンプがあります。
3Dおよび512のサブデータセットがある場合、合計1536の変数平均の各サブデータセットから3つの変数平均を結合できます。 次に、-1、-1 / 3、1 / 3、および1でバンプが表示されます。
Q:test_pred = pds [:、3] + pds [:、4] + pds [:、5]
target = 1がクラスター3,4および5にあることをどのようにして知りましたか? 0,1,2に該当する可能性があります
A:バイナリ分類では、1つのクラスに属する観測値の確率のみを予測します(この場合、ターゲット= 1またはクラスター3,4,5にあります)。
次に、任意の特定の観測について、クラスター0,1,2(またはターゲット= 0)にある確率は、単純に1-Pr(ターゲット= 1)です。
ここで、target = 0に関係なくtarget = 1のクラスターを見つけます
train4 = comb[ np.argwhere(all_y==1).flatten(), :]
clf = GaussianMixture(n_components=3).fit(train4) #randomness
clusters[ np.argwhere(all_y==1).flatten(), 3:] = clf.predict_proba(train4)
このclfは、all_y = target = 1のクラスターのみを検出します。その後、predict_proba()は、これら3つのクラスターのいずれかにある確率を変数クラスターの列3、4、5に入れます。 与えられた観測値がクラスターの列3、4、または5にある可能性が最も高い場合(つまり、これらの列の値が最大である場合)、後の変数cluster2は3、4、または5になります。 したがって、clusters2 = 3、4、5はtarget = 1を表します。
Q:可能であれば、以下のコード、特に最初の行と4番目のコードがどのように、何をしているのかを教えてください
for j in range(5): clusters[:,j+1] += clusters[:,j]
rand = np.random.uniform(0,1,clusters.shape[0])
for j in range(6): clusters[:,j] = clusters[:,j]>rand #randomness
clusters2 = 6 - np.sum(clusters,axis=1)
# IF IMBALANCED TRY AGAIN
least = pd.Series(clusters2).value_counts().min(); ct += 1
A:
変数クラスターには6つの列があります。各列の値(0、1、2、3、4、5)は、そのクラスター内にある確率(0、1、2、3、4、5)を表します。ここに例があります
0.99 0.01 0.0 0.0 0.0 0.0
0.0 0.0 0.0 1.0 0.0 0.0
0.0 0.85 0.0 0.15 0.0 0.0
行0、1、2は観測0、1、2です。観測0がクラスター0に存在する確率0.99とクラスター1に存在する確率0.01を持っていることに注意してください。
ここで、各観測がどのクラスターにあるかを判断する必要があります。簡単な方法は、各行の最大値を見つけることです(すなわち、clusters2 = np.argmax(clusters、axis = 1)、clusters2 = [0、3、1] )。その代わりに、私はトリッキーなことをします。
最初に、各列とその前の列を繰り返し追加します
0.99 1.0 1.0 1.0 1.0 1.0
0.0 0.0 0.0 1.0 1.0 1.0
0.0 0.85 0.85 1.0 1.0 1.0
次に、0から1の間のx個の乱数を選択します。xは行数です。たとえば、0.7、0.5、および0.1を選択します。次に、行0のどの数字が0.7より大きいかをマークします。行1のどの数字が0.5より大きいか。行2のどの数値が0.1より大きいか
True True True True True True
False False False True True True
False True True True True True
最後に、観測0はクラスター6-行0のTrueの数= 0です。観測1はクラスター6-行1のTrueの数= 3観測2はクラスター6-行2のTrueの数= 1 。したがって、clusters2 = [0、3、1]は上記のcluster2と同じです。ただし、この方法ではランダム性のため、結果がわずかにランダム化されます。
では、今度は不均衡な場合の再試行について説明します。すべての観測がどのクラスターにあるかを決定した後、6つのクラスターのそれぞれに含まれる観測の数をカウントします。理想的には、各クラスターに1024/6 = 170の観測値があるはずです。 150未満のグループがある場合、GMMが台無しになったため、プロセス全体を再度実行します。