好きな曲線を描くときは区間を分けてベジェ曲線を描き繋げることで近似できるが、たった1本のベジェ曲線ではどんな曲線が描けるのだろうか。
これを知っておけば、目的の曲線をなるべく簡潔に描いたりできるし、逆に不可能な曲線を作ろうとして試行錯誤する徒労を減らしたりもできる。
数式から作成
3次のベジェ曲線は以下の式で表される。
\vec{r}(s) = (1-s)^3 \vec{r}_0 + 3s(1-s)^2 \vec{r}_1 + 3s^2(1-s) \vec{r}_2 + s^3 \vec{r}_3 \qquad \left( 0 \le s \le 1 \right)
$\vec{r}_0$ ~ $\vec{r}_3$ は順に始点・第1制御点・第2制御点・終点であり、パラメーター $s$ を変化させながら4点の重み付き平均の場所をプロットしていることになる。
$s$ に着目すると3次式であるため、式変形するとベジェ曲線は以下の媒介変数表示が可能となる1。裏を返せば、この形で表現できない曲線はベジェ曲線で正確に描けない2。
\vec{r}(t)
=
\left(
\begin{array}{c}
x(t) \\
y(t) \\
\end{array}
\right)
=
\left(
\begin{array}{c}
a_3 t^3 + a_2 t^2 + a_1 t + a_0 \\
b_3 t^3 + b_2 t^2 + b_1 t + b_0 \\
\end{array}
\right)
\quad \left( t_1 \le t = (1-s) t_1+s t_2 \le t_2 \right)
このとき4点は以下のように逆算できる。
- 始点: $\vec{r}_0 = \vec{r}(t_1)$
- 第1制御点: $\vec{r}_1 = \vec{r}(t_1) + \frac{\Delta t}{3} \frac{d\vec{r}}{dt}(t_1) \quad (\Delta t = t_2 - t_1)$
- 第2制御点: $\vec{r}_2 = \vec{r}(t_2) - \frac{\Delta t}{3} \frac{d\vec{r}}{dt}(t_2)$
- 終点: $\vec{r}_3 = \vec{r}(t_2)$
よく「端点から制御点への方向はベジェ曲線の端の接線になる」と言われる通り、制御点の位置の式は端点の位置と微分で表されている。この式はさらに、目的の曲線を描くための端点から制御点までの距離も与えている。
以降では具体的な曲線をいくつか実際に描いてみる。
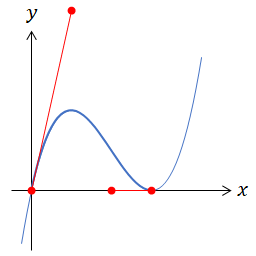
3次関数
高校数学の微分・積分で出てくる曲線。教科書のグラフは1本のベジェ曲線で正確に再現できることになる。
$x(t) = t$ としてしまえばいいので、始点・第1制御点・第2制御点・終点の4点をx軸の方向には等間隔にとると描ける。
30cm四方の厚紙を用意し、四隅から $x$ cm四方の正方形を切り取って蓋のない容器を組み立てる。容積を最大にするには $x$ をいくつにすればよいか。
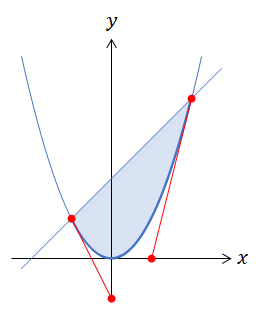
放物線
3次関数が描けるということは、2次関数である放物線も同じ方法で描ける。
放物線 $y=x^2$ と直線 $y=x+2$ が囲む領域の面積はいくらか。
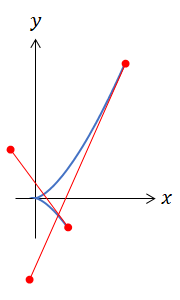
semicubical parabola
もう少し複雑な例として $y^2 = x^3$ を考えてみる。これは $\left( x(t), y(t) \right) = \left( t^2, t^3 \right)$ と表せるので、3次関数や放物線での描き方の応用になる。仮想的な軸 w を加えて $\left( w(t), x(t), y(t) \right) = \left( t, t^2, t^3 \right)$ とみるとヒントになるかもしれない。
この曲線の特徴である尖点が原点に現れている。尖点ができる条件は後ほど改めて扱う。
応用:ベジェ曲線の外挿
冒頭の $\vec{r}(s)$ は $0 \le s \le 1$ の範囲外まで計算すれば曲線を外挿できる。 $t = s$ とおいて新しい制御点 $\vec{r}'_0$ ~ $\vec{r}'_3$ を計算すればいい。
\begin{align}
\vec{r}(t) &= (1-t)^3 \vec{r}_0 + 3t(1-t)^2 \vec{r}_1 + 3t^2(1-t) \vec{r}_2 + t^3 \vec{r}_3 \\
\frac{1}{3} \frac{d\vec{r}}{dt}(t) &= (1-t)^2 \left( \vec{r}_1 - \vec{r}_0 \right) + 2t(1-t) \left( \vec{r}_2 - \vec{r}_1 \right) + t^2 \left( \vec{r}_3 - \vec{r}_2 \right) \\
\end{align}
例えば円弧を描くのにもベジェ曲線は使われるが、それを外挿するとどんな曲線になるのだろうか。試しに円周の1/4を描く線を伸ばしてみると、以下のようにαの形になる。
曲線の特徴から作成
すぐに数式で表せる曲線であれば前節の方法で問題ないが、そうはいかないことも多い。ここでは要求する曲線の特徴から制御点の位置を直接決められるものをいくつか扱う。
記事中では簡単のため単純なパラメーターで描くが、線形変換(平行移動・拡大縮小・回転・剪断変形)してもベジェ曲線の性質は変わらないので、色々な形のところで使える。
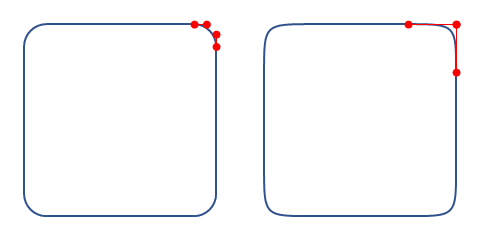
両端が曲率ゼロ
2本の直線を滑らかにつなぐ緩和曲線として使える。作り方は簡単で、2つの制御点を重ねるだけ。
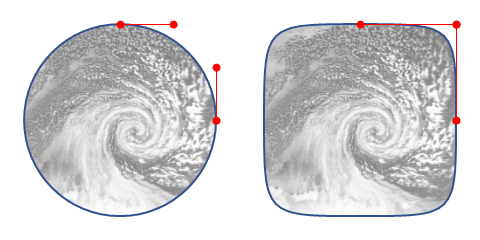
角丸正方形を作る際は角に円を使うと思う。しかしそうしてできた図形は直線が円に変わるところが微妙に滑らかに見えない。そこで円の代わりに両端が曲率ゼロの緩和曲線を使うと、曲率が滑らかに変化するため、直線から曲線に移る部分に違和感を持ちにくい。(曲率の話は、Appleのデザインについて扱ったテレビ番組で聞いた気がする)
直線部分をなくして丸い正方形をつくると、squircleという図形(の n=5.2 くらい)に近いものができる。正方形のアイコンを円で切り取ると面積が約 21% 減るが、この図形はたったの 5% しか減らないので元の絵をほぼ残したまま丸みを持たせられる。
正方形だけでなく他の多角形に使ってみても面白いかもしれないが、キリがないので1つの例でやめておく。
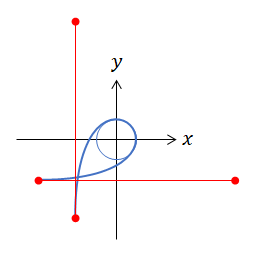
尖点あり
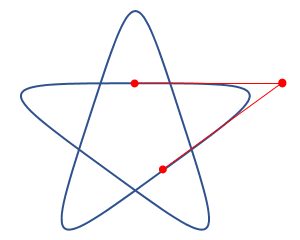
ベジェ曲線をいじっていると、ときどき曲線が鋭くとがることがある。この条件を知りたい。(この条件はまた、ベジェ曲線がループを作るかどうかの境目でもある。)
尖点を持つ必要条件は、冒頭のベジェ曲線の数式で $\frac{d\vec{r}}{ds}(s_0)=0$ となる $s_0$ が存在することである(厳密には微分した方向が前後で変わることも確かめなければいけない)。
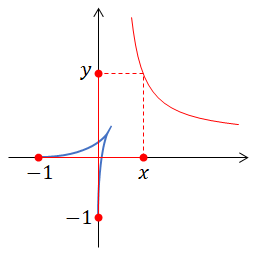
下図のようにベジェ曲線の4点の位置を $(-1,0)$, $(x,0)$, $(0,y)$, $(0,-1)$ と簡略化して考えると、制御点の座標に関しての条件式が出る。
\left( x - \frac{1}{3} \right) \left( y - \frac{1}{3} \right) = \frac{4}{9} \quad \left( x > 0 \: \rm{or} \: y > 0 \right)
条件式(図の赤い曲線)は、原点から少しずらした双曲線だった。semicubical parabolaの節で描いた図も、座標変換して形を整えてあげればこの条件通りの制御点配置になっている(はず)。
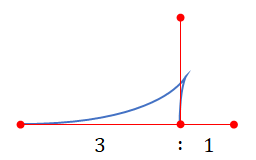
ところで、条件式で $x \to 1/3$ と極限をとると $y \to \pm \infty$ になってしまうが、これにも意味がある。この場合は座標変換することで特殊ケースを導ける。 y 方向が有限になるように縮小すると終点が原点に来るので、「ベジェ曲線の端点が相手の端点-制御点の線分上にあり、3:1で内分する」という条件を表す。
(端点の座標成分を -1 に固定せず、 a, b などのパラメーターにして考えたほうが簡単だったかも…)