誕生日のパラドックスとは、「$n$ 人が集まったときにその中に同じ誕生日の組ができる確率 $p(n)$ を求める」といった問題(誕生日問題)が、直感に合わないほど大きな確率をとるというもの。30人くらいのメンバーで実際に同じ誕生日の組ができるか試すと盛り上がる。一方でハッシュ関数の衝突という話に置き換えると、一見ハッシュ値の満杯にほど遠いメンバー数でもわりと衝突が起きやすいということを示していて、衝突を避けるにはハッシュ値を十分に大きくする必要がある。
ところで、この問題を考えるときはふつう「365日どれでも同じ確率」という前提をおくが、出生数は「9月に多い」「休日は少ない」などのばらつきがある。確率が偏っていると同じ誕生日の組ができる確率は上がるはずである。これを実際に求めてみる。
確率一様の場合(おさらい)
「少なくとも1つある」という場合の確率を求めるときは、正反対の「全くない」という確率を求めて1から引くと簡単な場合が多い。誕生日問題では「$n$ 人の誕生日が全て異なる確率 $\bar{p}(n)=1-p(n)$」を求めればいいことになる。メンバーの誕生日がとあるパターン(例えばAが1/1生まれ、Bが1/2生まれ、Cが1/3生まれ、…)になる確率はどれも $\frac{1}{365^n}$、誕生日が全て異なる場合の数は $_{365}P_{n}$ であるので、
1-p(n) = \frac{_{365}P_{n}}{365^n} = \frac{365!}{365^n \left( 365-n \right)!}
N = 365
a = 1.0 / N
p_bar = (1..N).inject([1]) { |ary,n| ary << ary.last * (N - n + 1) * a }
確率が一様でない場合
誕生日が日付 $i$ である確率を $a_i$ (配列の添字の都合で $0 \le i < N$ )とする。一様のときと同じように、全員の誕生日が異なる確率を先に求める。
テストデータ
2014年の出生数1を基に、確率分布の配列 $a とその長さ N を作成する。実在しない日については人数をゼロとしているが、計算上問題は無い。
x = [
1873, 1883, 1948, 2430, 2193, 3156, 3390, 3112, 2966, 3058, 2309, 1999, 2022, 3086, 3323, 3136, 3078, 2317, 1941, 2919, 3108, 3142, 3047, 3007, 2300, 1965, 2979, 3136, 2905, 3001, 2843,
2288, 2013, 2864, 3032, 2922, 2800, 3043, 2204, 2013, 2831, 2088, 2980, 3046, 2870, 2215, 1906, 2841, 3090, 2791, 2896, 2800, 2200, 1932, 2705, 3010, 2885, 2789, 2843, 0, 0, 0,
2230, 1886, 2922, 2967, 2887, 2819, 2797, 2238, 1934, 2908, 2915, 2918, 2764, 2878, 2215, 1896, 2830, 3112, 2899, 2880, 1928, 2028, 1925, 2776, 3047, 2944, 2683, 2770, 2019, 1879, 2446,
2354, 3177, 3065, 2818, 2149, 1813, 2647, 3018, 2730, 2925, 3004, 2135, 1872, 2714, 3174, 2904, 2764, 2703, 2124, 1857, 2736, 3088, 2962, 2915, 2930, 2157, 1897, 3049, 2067, 3086, 0,
3436, 3345, 2079, 1964, 2043, 1942, 2974, 3265, 3199, 2374, 2008, 2999, 3020, 3060, 3033, 2993, 2259, 1985, 2808, 3097, 2818, 2886, 2829, 2231, 1882, 2877, 3124, 2860, 2835, 2889, 2196,
1977, 2858, 3156, 2938, 2825, 3021, 2232, 1887, 2810, 3220, 2897, 2996, 2999, 2233, 2009, 3038, 3174, 2898, 2932, 2916, 2316, 1968, 2861, 3135, 3049, 2937, 2935, 2221, 2006, 2957, 0,
3266, 3189, 3085, 3028, 2354, 2055, 3139, 3207, 3055, 3067, 3039, 2326, 2040, 2912, 3135, 3316, 3223, 3227, 2425, 2064, 2116, 3306, 3615, 3191, 3215, 2515, 2059, 2967, 3252, 3029, 3099,
3159, 2371, 2121, 3028, 3331, 3236, 3164, 3284, 2354, 2114, 3017, 3482, 3064, 2721, 2725, 2414, 2159, 3129, 3256, 3257, 3041, 3113, 2291, 2156, 3007, 3289, 3134, 3052, 2892, 2377, 1994,
3038, 3234, 3285, 2946, 3172, 2325, 1950, 3158, 3481, 3403, 3186, 3273, 2410, 2244, 2276, 3394, 3588, 3500, 3538, 2638, 2262, 3372, 2544, 3415, 3609, 3436, 2676, 2297, 3276, 3383, 0,
3330, 3166, 3256, 2480, 2086, 3037, 3238, 3180, 3097, 3392, 2332, 2028, 2051, 3141, 3246, 3119, 3080, 2248, 2036, 3022, 3211, 3083, 3011, 3118, 2301, 1991, 2961, 3175, 3009, 3012, 3155,
2422, 2094, 2010, 3177, 3345, 3010, 3188, 2322, 2046, 2941, 3319, 2998, 2936, 2936, 2268, 1984, 2887, 3120, 3016, 3085, 3054, 2380, 1951, 1958, 3148, 3185, 3070, 3021, 2172, 1950, 0,
2887, 3117, 3048, 2853, 3005, 2238, 2008, 2928, 3188, 3020, 2917, 3048, 2275, 1964, 2993, 3256, 3144, 3131, 3109, 2291, 2099, 3304, 2124, 3392, 3748, 3583, 2423, 1895, 2680, 2372, 2003,
]
sum = x.inject(:+)
$a = x.collect { |x_i| x_i.to_f / sum }
N = $a.size
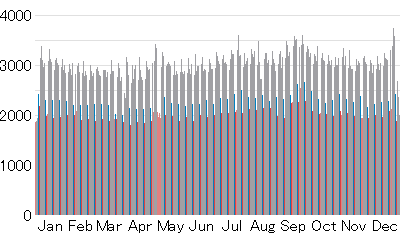
ちなみにグラフ化すると以下の通り。平日(灰色)は土・日・祝日(青・赤・ピンク)より明らかに1日の出生数が多い。
素直に計算
皆がとある異なる誕生日のパターンになる確率はその誕生日に依存するので、個別に計算して足し合わせる。例えばA, B, Cの3人の場合は、
全員異なる誕生日となる確率 =
(Aが1/1、Bが1/2、Cが1/3である確率)
+ (Aが1/1、Bが1/2、Cが1/4である確率)
+ ...
+ (Aが12/31、Bが12/30、Cが12/29である確率)
1 - \left. p(n) \right|_{n=3} = a_0 a_1 a_2 + a_0 a_1 a_3 + \cdots + a_{N-1} a_{N-2} a_{N-3}
これを計算するには、確率分布の配列 $a から n 個を取り出して並べた数の積を計算し、それを全て足し合わせればいい。
require './test_data'
# 安全のため、p_bar[3]まで求めて終了させる
p_bar = (0..3).collect { |n| $a.permutation(n).inject(0) { |sum,ary| sum + ary.inject(1, :*) } }
しかし、この方法は n = 3 でも時間がかかり、30人の場合などには到底対応できない。順列から組み合わせに変えることもできるが根本的な解決にはならない。
計算の改善
各順列の積を足し合わせるという式を $a_{N-1}$ を含む項と含まない項に分けてみると、$N$ がより小さい問題の計算結果を利用して求められることが分かる。
\begin{align}
\left. f(N, n) \right|_{n=3} &= a_0 a_1 a_2 + a_0 a_1 a_3 + \cdots + a_{N-1} a_{N-2} a_{N-3} \\
&= \left( a_0 a_1 a_2 + a_0 a_1 a_3 + \cdots + a_{N-2} a_{N-3} a_{N-4} \right) + \left( a_0 a_1 + a_0 a_2 + \cdots + a_{N-2} a_{N-3} \right) n a_{N-1} \\
&= f(N-1, n) + n a_{N-1} f(N-1, n-1)
\end{align}
これを再帰で実装する。高速化のために、同じ計算を何度もしないようメモ化する。
require './test_data'
# $a[0,m]からn個を並べて掛けた数の総和を求めるメソッド
$table = Array.new(N + 1) { Array.new(N + 1) }
def f(m, n)
$table[m][n] ||= (
if n == 0
1
elsif m < n
0
else
f(m - 1, n) + n * $a[m-1] * f(m - 1, n - 1)
end
)
end
p_bar = (0..N).collect { |n| f(N, n) }
さらに改善
$table を事前に全て埋めてしまえば、再帰呼び出しが無くなるうえに p_bar[0..N] を一度に求めることができる。以下のコードでは、順序に気を付けて p_bar を更新することで、2次元のテーブルを作らずに結果を求めている。
require './test_data'
p_bar = Array.new(N + 1, 0)
p_bar[0] = 1
(1..N).each do |m|
(1..m).reverse_each do |n|
p_bar[n] += n * $a[m-1] * p_bar[n-1]
end
end
計算結果
$p(n)$ の値を比較してみる。( 1 - p_bar[n] であることに注意)
| $n$ | 一様分布 | テストデータ | 増分 |
|---|---|---|---|
| 20 | 0.411438 | 0.420638 | 0.009200 |
| 30 | 0.706316 | 0.716744 | 0.010428 |
| 40 | 0.891232 | 0.898074 | 0.006842 |
偏りのあるテストデータの方が、同じ誕生日の組ができる確率がたしかに高くなっている。
応用
上の例では1年間のデータのみ使ったため、同じ年に生まれた人たちの集まりでのみ有効である。4/2~翌年4/1のデータを用意すれば、同級生で試した場合の確率が求まる。
複数年のデータを日付ごとに足したものを用いれば、学年が混ざっている集団に対しての確率が求まる。曜日による出生数の偏りがならされるため増分は少なくなるものの、やはり一様分布より高い確率となる。
閏年かどうかは関係なく計算できる。平年であれば2/29生まれは0人と考えればいい。
そもそも上の例の通り、実在しない日を作っても人数をゼロとしておけば正しく計算できる。ゼロを含むデータに対して確率を計算すると、大きな n に対して p_bar[n] == 0.0 となるが、これは鳩の巣原理を反映していると考えられる。2
実際の出生数を使わずに単純な分布を与えてもいい。一様分布はもちろんできるし、平日と休日の2値にしたり、2/29だけ0.25倍の分布もできる。
誕生日以外だと、ガチャの確率分布を与えれば $n$ 回引いてダブる確率を求めたりもできる。(補正がかかっていれば計算とは合わないが)
注意点としては、この計算は $N$ の2乗に比例した時間がかかるので、個数の多い確率分布に対しては実行しないほうがいい。