Rubyで「フロイドの循環検出法」を実装 #Ruby

たまに使うことがあるので、作ったコードを記録しておく。またこの機会に、アルゴリズムの動作原理を自分なりにまとめて理解する。

Rubyのコード

# 漸化式 x_{n+1} = f(x_{n}) で与えられる列が循環を持つとき、
# 循環に入るまでの長さ l と循環の長さ m を測る
def find_cycle(x0, limit = nil, &f)
    # 循環検出の回数制限を設定（終端 nil または Float::INFINITY で無限）
    seq = 1..limit

    # step1: 循環を検出する
    x = y = x0
    k = seq.find { (x = f[x]) == (y = f[f[y]]) }
    raise "failed to detect a cycle" unless k

    # step2: 循環に入るまでの長さを測る
    x = x0
    l = (x == y) ? 0
      : seq.find { (x = f[x]) == (y = f[y]) }

    # step3: 循環の長さを測る
    m = seq.find { (x = f[x]) == (y = f[f[y]]) }

    [l, m]
end

if $0 == __FILE__
    # テスト： x_{n+1} ≡ x_{n} * 2 (mod 360), x_{0} = 133
    l, m = find_cycle(133) { |x| x * 2 % 360 }
    p [l, m]

    # x_{l} == x_{l+m} （かつ x_{l-1} != x_{l+m-1} ）になるはず
    ary = (l + m).times.inject([133]) { |a, _| a << (a.last * 2 % 360) }
    ary.each_with_index { |x, i| puts "%3d %4d" % [i, x] }
end

アルゴリズムの仕組み

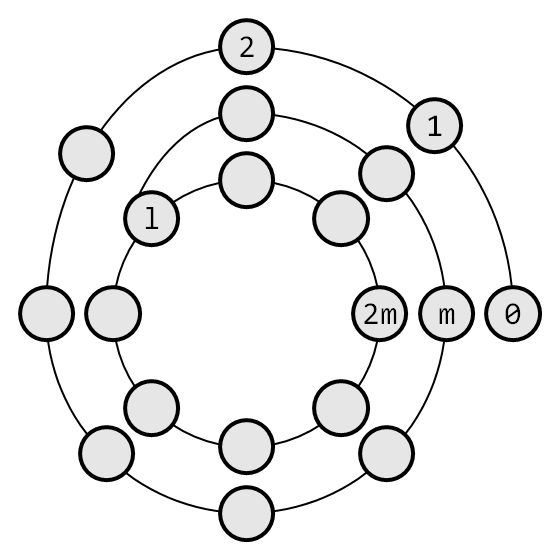
以下のグラフ（ l = 11, m = 8 ）の図で説明する。

循環節のノードを円形に配置し、非循環節はノードが揃うように「巻き付けて」いる。結果として m の倍数番目のノード（ 0, m, 2m ）は円の中心から見て同じ方向に並んでいる。

step1: 循環を検出する
- x と y は共にスタート地点（ノード 0 、値 x0 ）から始める
- x は1つずつ、 y は2つずつ進める
  - x が1周してノード m に来れば y は2周してノード 2m に来る
  - このように、 x と y はノード 0 と同じ方向で必ず並ぶ
- x が循環に入ればいつか必ず y が追いつき x == y になる
  - この位置はやはりノード 0 と同じ方向、つまり m の倍数
  - あくまで m の倍数であり、循環の長さ m そのものではない可能性があることに注意
step2: 循環に入るまでの長さを測る
- x だけスタート地点に戻し、 y はstep1終了時（循環節にある m の倍数のノード）から続ける
- x も y も1つずつ進める
  - 円の中心から見て x と y は常に同じ方向にいて並走する
- すると、循環に入った瞬間（ノード l ）で必ず x == y になる
step3: 循環の長さを測る
- x と y は共に循環の中（簡単なのはstep2終了時）から始める
- x は1つずつ、 y は2つずつ進める
- この場合、step1と異なり x がちょうど1周で必ず x == y になる

Rubyで「フロイドの循環検出法」を実装

Rubyのコード

アルゴリズムの仕組み

参考