3次ベジェ曲線の制御点をうまく設定することが苦手なので、端点の曲率(と接線)を指定して制御点を求めようとした。
概要
- 端点の曲率を指定して3次ベジェ曲線の制御点の位置を求める方程式を導いた
- 任意の数値を入れて解くことはまだ
- 接線の交点の位置によっては解なし
- 方程式が簡単になる状況で解いて、曲線を近似してみた
- 割ときれいに描けて、精度もまあまあ(偶然?)
- さすがに曲率よりも別の条件を置いたほうが高精度
曲率の数式
曲線について以下の式が成り立つ。
\frac{d^2 \vec{r}}{ds^2} = \frac{d \vec{t}}{ds} = \frac{\vec{n}}{R}
- $s$:曲線に沿った距離
- $\vec{r}(s)$:曲線上の一点を表す位置ベクトル
- $\vec{t}(s)$:単位接ベクトル
- $\vec{n}(s)$:単位法線ベクトル(カーブの内側向き)
- $R(s)$:曲率半径(曲率の逆数)
実際の曲線は、「曲線に沿った距離」の関数で表すのは面倒なので、別のパラメーターで $s$ を置換する。
媒介変数表示の曲線
2次元平面上の曲線はパラメーター $u$ を用いて $\vec{r}(u) = \left( x(u), y(u), 0 \right)$ と表せる(外積を使いたいので3次元にしている)。$u$ 微分をプライムで表すと
\begin{align}
s(u)
&= \int_{0}^{u} \left| \vec{r}'(u) \right| du \\
\vec{t}
= \frac{d \vec{r}}{ds}
&= \frac{\vec{r}'}{|\vec{r}'|} \\
\frac{\vec{n}}{R}
= \frac{d^2 \vec{r}}{ds^2}
&= \frac{\left( \vec{r}' \times \vec{r}'' \right) \times \vec{r}'}{|\vec{r}'|^4}
\end{align}
ベジェ曲線での計算のために、長さが曲率半径である接ベクトル $R\vec{t}$ というのを求めておく。
\begin{align}
|R|\vec{t}
&= \frac{|\vec{r}'|^3}{|\vec{r}' \times \vec{r}''|} \frac{\vec{r}'}{|\vec{r}'|} \\
&= \frac{|\vec{r}'|^2}{|\vec{r}' \times \vec{r}''|} \vec{r}' \\
R \vec{t}
&= \frac{|\vec{r}'|^2}{(\vec{r}' \times \vec{r}'')_z} \vec{r}'
\end{align}
最後の式は $\vec{r}$ が2次元の曲線であることを利用していて、右手系での左カーブを正曲率と取り決めることでカーブの方向を符号に反映させている。添字 $z$ はベクトルの $z$ 成分という意味で、書き下せば $(\vec{r}' \times \vec{r}'')_z = x' y'' - y' x''$ 。
陽関数表示の曲線
正弦曲線などの接線と曲率半径を求めるときのために補足。
既に媒介変数表示の場合を求めているため、$x$ をパラメーターとして $\vec{r}(x) = \left( x, f(x), 0 \right)$ と表せばいい。
\begin{align}
\vec{r}'(x)
&= \left( 1, f'(x), 0 \right) \\
R \vec{t}
&= \frac{|\vec{r}'|^2}{f''(x)} \vec{r}'
\end{align}
ベジェ曲線
よく使われる3次ベジェ曲線の式は、始点 $\vec{r}_0$、制御点 $\vec{r}_1, \vec{r}_2$、終点 $\vec{r}_3$ として、
\vec{r}(u) = (1-u)^3 \vec{r}_0 + 3u(1-u)^2 \vec{r}_1 + 3u^2(1-u) \vec{r}_2 + u^3 \vec{r}_3
これを $u$ で微分して、$\vec{r}_j - \vec{r}_i = \vec{r}_{ij}$ とまとめると、
\begin{align}
\frac{1}{3} \vec{r}'(u)
&= (1-u)^2 \vec{r}_{01} + 2u(1-u) \vec{r}_{12} + u^2 \vec{r}_{23} \\
\frac{1}{6} \vec{r}''(u)
&= (1-u) \left( \vec{r}_{12} - \vec{r}_{01} \right) + u \left( \vec{r}_{23} - \vec{r}_{12} \right) \\
\frac{1}{18} \vec{r}' \times \vec{r}''
&= (1-u)^2 \vec{r}_{01} \times \vec{r}_{12} + u(1-u) \vec{r}_{01} \times \vec{r}_{23} + u^2 \vec{r}_{12} \times \vec{r}_{23}
\end{align}
制御点→端点の曲率
制御点が決まっているとして、端点 $u=0,1$ の $R\vec{t}$ を求めてみる。(2次元曲線のため $\vec{r}$ のz成分はゼロとしていることに注意)
\begin{align}
\left. R \vec{t} \right|_{u=0}
&= +\frac{3}{2} \frac{|\vec{r}_{01}|^2}{(\vec{r}_{01} \times \vec{r}_{12})_z} \vec{r}_{01} \\
\left. R \vec{t} \right|_{u=1}
&= -\frac{3}{2} \frac{|\vec{r}_{23}|^2}{(\vec{r}_{23} \times \vec{r}_{12})_z} \vec{r}_{23}
\end{align}
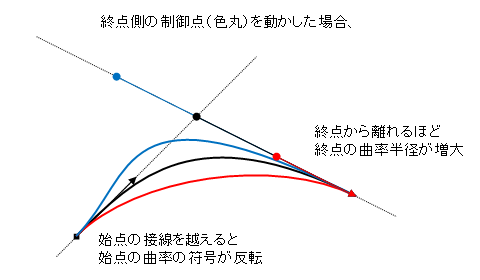
この式から分かることをいくつか挙げると、
- 端点と制御点を結ぶ直線が、端点での曲線の接線になる
- 制御点を端点から離すほど、端点での曲率半径が大きくなる
- 曲率半径は端点-制御点の距離の2乗に比例する
- 反対側の制御点をいじっても端点での曲率が変化する
- 制御点が接線を越えると曲率の符号が逆転する。接線上なら曲率ゼロ(曲率半径∞)
- 曲率半径は制御点と接線の距離に反比例する
また、曲率の符号については制限がかかることがある。上の図では終点から見て接線の交点が制御点と同じ方向にあるため、制御点が始点の接線を越えることができて、始点の曲率は正負の両方をとれる。しかしもし接線の交点が制御点と逆方向なら、制御点が始点の接線を越えられず、始点の曲率は正負のどちらかに決まってしまう。
端点の曲率→制御点
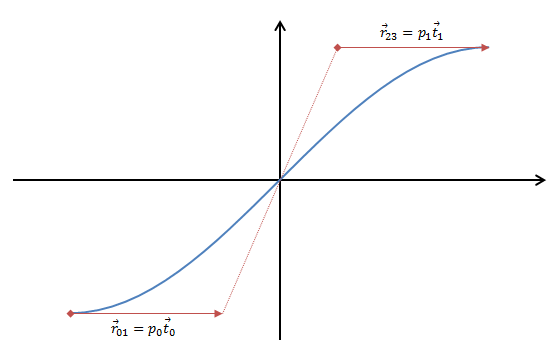
逆に端点 $u=0,1$ の $R\vec{t}$ が決まっている場合は、前節の式を逆に解くことで制御点を計算することができる。$\vec{r}_{01} = p_0 \vec{t}_0$, $\vec{r}_{23} = p_1 \vec{t}_1$($p_0, p_1 \ge 0$)とおき、$\vec{r}_{12} = \vec{r}_{03} - \vec{r}_{01} - \vec{r}_{23}$ を用いて整理すれば、端点-制御点の距離 $p_0, p_1$ についての方程式が得られる。
\begin{align}
\left( \vec{t}_0 \times \vec{r}_{03} \right)_z - p_1 \left( \vec{t}_0 \times \vec{t}_1 \right)_z &= +\frac{3}{2} \frac{p_0^2}{R_0} \\
\left( \vec{t}_1 \times \vec{r}_{03} \right)_z + p_0 \left( \vec{t}_0 \times \vec{t}_1 \right)_z &= -\frac{3}{2} \frac{p_1^2}{R_1}
\end{align}
グラフで示せば、縦横2つの放物線(または直線)の第1象限での交点を求めることになる。これの一般解を求められるのかはまだよく分かっていないが、特殊な状況であれば簡単に求められたりする。
実例
単純な曲線について、端点の曲率を合わせることで近似してみる。
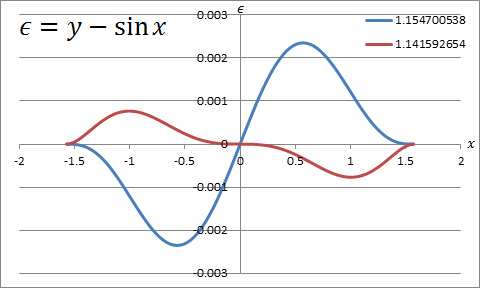
正弦曲線の近似
$y = \sin{x}$ を谷から山まで描いてみる。$y$ 方向の誤差は 0.25% 未満。
R_0 = +1, \: R_1 = -1 \\
\vec{t}_0 = \vec{t}_1 = (1, 0) \\
\vec{r}_{03} = (\pi, 2) \\
\to p_0 = p_1 = \frac{2}{\sqrt{3}}
なお、$p_0 = p_1 = \pi-2$ (変曲点での傾きが等しくなる)とすれば誤差はその1/3程度となる。また実際の描き方を調べてみると、より多くの区間に分割して細かく近似する方法がよく紹介されている。
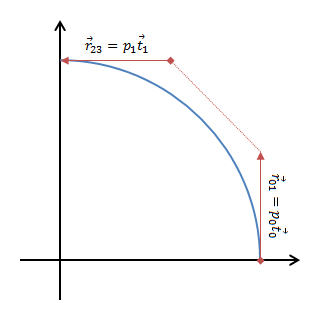
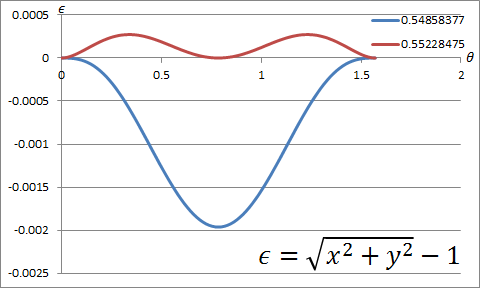
円弧の近似
原点中心で $(1, 0)$ から $(0, 1)$ までの円弧を描いてみる。半径の誤差は 0.2% 未満。
R_0 = R_1 = 1 \\
\vec{t}_0 = (0, 1), \: \vec{t}_1 = (-1, 0) \\
\vec{r}_{03} = (-1, 1) \\
\to p_0 = p_1 = \frac{\sqrt{7}-1}{3}
一般のソフトウェアで使われる円弧の近似は $p_0 = p_1 = \frac{4}{3} (\sqrt{2}-1)$ で、誤差は 0.03% 未満。これはベジェ曲線の中央の点も円弧と一致するように定めたもの。