四元数(クォータニオン)を4次元空間の幾何に使ってみるお話。4次元空間での回転の計算に強いので、回転対称性が高い正多胞体を扱う際は特に便利なはず。
サンプルコード
難しい話は後回しにして、4次元正多胞体の頂点を実際にプログラムで計算してみる。
require 'quaternion_c2'
require 'quadratic_number'
SQRT5 = Quadratic[5].new(0, 1)
PHI = (1 + SQRT5) / 2 # golden ratio
q1 = -1
q2 = Complex::I
q3 = Quaternion::J
q4 = Quaternion(1, 1, 1, 1) / 2
q5 = Quaternion(PHI, 1, 1/PHI, 0) / 2
# calc q1**m1 * q2**m2 * q3**m3 * q4**m4 * q5**m5
vertices = [1]
[q1, q2, q3, q4, q5].zip([2, 2, 2, 3, 5]) do |qi,ni|
vertices_rot = vertices.dup # v * (qi ** 0)
(1...ni).each do |mi|
vertices_rot.map! { |v| v * qi }
vertices.concat(vertices_rot)
end
end
vertices_5cell = [
1,
Quaternion(-1, -SQRT5, -SQRT5, -SQRT5) / 4,
Quaternion(-1, -SQRT5, SQRT5, SQRT5) / 4,
Quaternion(-1, SQRT5, -SQRT5, SQRT5) / 4,
Quaternion(-1, SQRT5, SQRT5, -SQRT5) / 4,
]
vertices_8cell = vertices[0...16]
vertices_16cell = vertices[0...8]
vertices_24cell = vertices[0...24]
vertices_120cell = vertices_5cell.product(vertices).map { |v5,v600| v600 * v5 }
vertices_600cell = vertices
def verify(vertices, name)
num_vertices = vertices.size
edges_and_diagonals = vertices.
combination(2).
group_by { |a,b| Math.sqrt((b - a).abs2.to_f) }
edge_length = edges_and_diagonals.keys.min
num_edges = edges_and_diagonals[edge_length].size
puts "%8s has %4d vertices and %4d edges" % [name, num_vertices, num_edges]
end
puts "### verifications ###"
verify(vertices_5cell, "5-cell")
verify(vertices_8cell, "8-cell")
verify(vertices_16cell, "16-cell")
verify(vertices_24cell, "24-cell")
verify(vertices_120cell, "120-cell") # takes a long time
verify(vertices_600cell, "600-cell")
puts
puts "### all vertices of a 600-cell ###"
vertices_600cell.each_with_index { |v,i| puts "#{i}\t#{v}" }
puts
### verifications ###
5-cell has 5 vertices and 10 edges
8-cell has 16 vertices and 32 edges
16-cell has 8 vertices and 24 edges
24-cell has 24 vertices and 96 edges
120-cell has 600 vertices and 1200 edges
600-cell has 120 vertices and 720 edges
### all vertices of a 600-cell ###
0 1
1 -1
2 0+1i
3 0-1i
4 0+0i+1j+0k
5 0+0i-1j+0k
6 0+0i+0j+1k
7 0+0i+0j-1k
8 1/2+1/2i+1/2j+1/2k
9 -1/2-1/2i-1/2j-1/2k
...
22 -1/2-1/2i+1/2j-1/2k
23 1/2+1/2i-1/2j+1/2k
24 ((1/4)+(1/4)*√5)+((1/2)+(0/1)*√5)*i+((-1/4)+(1/4)*√5)*j+((0/1)+(0/1)*√5)*k
25 ((-1/4)-(1/4)*√5)-((1/2)+(0/1)*√5)*i-((-1/4)+(1/4)*√5)*j+((0/1)+(0/1)*√5)*k
...
118 ((1/2)+(0/1)*√5)+((-1/4)+(1/4)*√5)*i-((1/4)+(1/4)*√5)*j+((0/1)+(0/1)*√5)*k
119 ((-1/2)+(0/1)*√5)-((-1/4)+(1/4)*√5)*i+((1/4)+(1/4)*√5)*j+((0/1)+(0/1)*√5)*k
計算を楽にするため、Rubyの数値クラスを追加するライブラリを2つ使っている。
-
quaternion_c2(Quaternion)- 四元数を扱う
- 組み込みクラス
Complexを真似ているので同じように使える(→実装メモ)
-
quadratic_number(Quadratic[d])- $a+b\sqrt{d}$ という形の数を正確に表す
- 求めた2つの数を比較する際に、計算誤差を考慮しなくて済む
正多胞体の作り方と種類
正多胞体は低い次元から段階的に作ることができる。正多角形・正多面体のおさらいも兼ねてまとめておく。
2次元(正多角形)
2次元の場合は簡単に紙に描けるので分かりやすい。同じ長さの線分を何本か用意して、各頂点の内角が同じになるように端をつなげていく。
| 辺 | 頂点 | 隣の頂点 | 内角 | |
|---|---|---|---|---|
| 正三角形 | 3 | 3 | 2 | 60° |
| 正四角形 (正方形) |
4 | 4 | 2 | 90° |
| 正五角形 | 5 | 5 | 2 | 108° |
| 正六角形 | 6 | 6 | 2 | 120° |
| ... | ||||
| 正N角形 | N | N | 2 | 180°-360°/N |
| ... |
3次元(正多面体)
3次元の場合は、同じ正多角形を何枚か用意して、各頂点の形が同じになるように辺同士をつなげていく。展開図にすると分かりやすいが、丸く立体にするには頂点に集まった3枚以上の正多角形の角度の和が360°未満な必要があるので、作れる正多面体の種類には限りがある。
| 面 | 辺 | 頂点 | 隣の頂点 (配置) | 二面角 | |
|---|---|---|---|---|---|
| 正四面体 | 正三角形 x 4 | 6 | 4 | 3 (正三角形) | 70.53° |
| 正六面体 (立方体) |
正四角形 x 6 | 12 | 8 | 3 (正三角形) | 90° |
| 正八面体 | 正三角形 x 8 | 12 | 6 | 4 (正四角形) | 109.47° |
| 正十二面体 | 正五角形 x 12 | 30 | 20 | 3 (正三角形) | 116.56° |
| 正二十面体 | 正三角形 x 20 | 30 | 12 | 5 (正五角形) | 138.19° |
4次元
4次元の場合も考え方は変わらない。同じ_正多面体_を何個か用意して、各頂点の形が同じになるように_面_同士を貼り合わせていく。_辺_に集まった3個以上の_正多面体_の角度(二面角)の和が360°未満でないといけないので、やはり種類には限りがある。
実際に作ってみると、要素の数は3次元と比べて桁違いに多い(2次元→3次元も桁違いだが)。これの全座標や隣り合う頂点などを楽に計算できないかというのが本記事の動機。
| 胞 | 面 | 辺 | 頂点 | 隣の頂点 (配置) | 二面角 | |
|---|---|---|---|---|---|---|
| 正五胞体 | 正四面体 x 5 | 正三角形 x 10 | 10 | 5 | 4 (正四面体) | 75.52° |
| 正八胞体 (超立方体) |
正六面体 x 8 | 正四角形 x 24 | 32 | 16 | 4 (正四面体) | 90° |
| 正十六胞体 | 正四面体 x 16 | 正三角形 x 32 | 24 | 8 | 6 (正八面体) | 120° |
| 正二十四胞体 | 正八面体 x 24 | 正三角形 x 96 | 96 | 24 | 8 (正六面体) | 120° |
| 正百二十胞体 | 正十二面体 x 120 | 正五角形 x 720 | 1200 | 600 | 4 (正四面体) | 144° |
| 正六百胞体 | 正四面体 x 600 | 正三角形 x 1200 | 720 | 120 | 12 (正二十面体) | 164.48° |
5次元以上
軽く触れておくと、5次元以上では二面角の制限から3種類だけ生き残る(△と□と◇)。頂点の座標は簡単に表せ、4次元ほど苦労しないと思う。
| ファセット (n-1 次元面) |
... | m次元面 (0≦m<n) | ... | 頂点 | 隣の頂点 (配置) | 二面角 | |
|---|---|---|---|---|---|---|---|
| n次元正単体 | n-1 次元正単体 x (n+1) |
m次元正単体 x ${}_{n+1}C_{m+1}$ |
n+1 | n (n-1 次元正単体) |
$\arccos{\tfrac{1}{n}}$ | ||
| n次元正測体 (超立方体) |
n-1 次元正測体 x 2n |
m次元正測体 x $2^{n-m} {}_{n}C_{m}$ |
2^n | n (n-1 次元正単体) |
90° | ||
| n次元正軸体 | n-1 次元正単体 x 2^n |
m次元正単体 x $2^{m+1} {}_{n}C_{m+1}$ |
2n | 2(n-1) (n-1 次元正軸体) |
$\arccos{\tfrac{2-n}{n}}$ |
双対について
上の表を見ると、例えば正八胞体と正十六胞体の胞・面・辺・頂点の数はちょうど逆順になっている。これは双対と呼ばれる関係の特徴で、どの多胞体にも当てはまり必ず相方がいる(自己双対の場合は自分自身)。
ある正多胞体の双対な正多胞体を作るには、ファセット(n-1 次元面)の中心に新しい頂点を置けばいい。正多面体の場合は例えばこのページに全てのパターンの絵が載っている。
本記事では細かく説明しないが、正百二十胞体を直接扱うのが難しいときは双対である正六百胞体を基準に考えると楽だったりする。
頂点の座標:組み合わせによる生成
書いてある座標について順序の並べ替え(置換)や符号の選び方を列挙することで、全ての点の座標を得られる。Wikipediaに載っているものを以下に並べた。
正五胞体
これは正単体なので、1次元多い5次元で作るほうが楽。
- $(1, 0, 0, 0, 0)$ の置換による5点
正八胞体
- $(\pm 1/2, \pm 1/2, \pm 1/2, \pm 1/2)$ の16点
正十六胞体
- $(\pm 1, 0, 0, 0)$ の置換による8点
正二十四胞体
正八胞体と正十六胞体が組み合わさったもので、4次元特有の正多胞体。
- $(\pm 1, 0, 0, 0)$ の置換による8点
- $(\pm 1/2, \pm 1/2, \pm 1/2, \pm 1/2)$ の16点
または、大きさは変わるが以下の座標でも作れる。
- $(0, 0, \pm 1, \pm 1)$ の置換による24点
正百二十胞体
どうやって見つけたのか不思議なくらい複雑。偶置換を使うので下側の3つは初期の並び順にも気を付けなければならない。
- $(0, 0, \pm 2, \pm 2)$ の置換による24点
- $(\pm 1, \pm 1, \pm 1, \pm \sqrt{5})$ の置換による64点
- $(\pm \phi^{-2}, \pm \phi, \pm \phi, \pm \phi)$ の置換による64点(φは黄金比)
- $(\pm \phi^{-1}, \pm \phi^{-1}, \pm \phi^{-1}, \pm \phi^2)$ の置換による64点
- $(0, \pm \phi^{-2}, \pm 1, \pm \phi^2)$ の偶置換による96点
- $(0, \pm \phi^{-1}, \pm \phi, \pm \sqrt{5})$ の偶置換による96点
- $(\pm \phi^{-1}, \pm 1, \pm \phi, \pm 2)$ の偶置換による192点
正六百胞体
正百二十胞体からするとだいぶ楽。座標に使われている数の arccos を度数法で計算してみると面白い。
- $(\pm 1, 0, 0, 0)$ の置換による8点
- $(\pm 1/2, \pm 1/2, \pm 1/2, \pm 1/2)$ の16点
- $(\pm \phi/2, \pm 1/2, \pm \phi^{-1}/2, 0)$ の偶置換による96点(φは黄金比)
頂点の包含関係
それぞれの正多胞体の座標を見比べると、ある正多胞体の頂点を抜き出して他の正多胞体を作れる場合があることに気付く。例えば正六百胞体の最初の24点は正二十四胞体の頂点の座標そのままである。計測しなければ分からないパターンも含めると以下のような関係があり、何と全ての4次元正多胞体が登場する。
- 正百二十胞体 (600点) ⊃ 正六百胞体 (120点) ⊃ 正二十四胞体 (24点) ⊃ 正八胞体 (16点) ⊃ 正十六胞体 (8点)
- 正百二十胞体 (600点) ⊃ 正五胞体 (5点)
この関係を利用すると、「簡単な正多胞体を回転コピーしてより複雑な正多胞体の頂点を作る」ことができ、特に太字で書いたものには相性がいい。4次元だと想像しにくいので3次元の例を挙げると、例えば正四面体を5個組み合わせて正十二面体の頂点を作ることができる(→compound of five tetrahedra)。
頂点の座標:四元数の積による生成
いよいよ本題。「簡単な正多胞体を回転コピーしてより複雑な正多胞体の頂点を作る」ことを実践する。
4次元空間での回転となれば四元数を使うのが楽。一般的な4次元回転 p → p' は2つの単位四元数 $q_L, q_R$ を使って $p' = q_L p q_R$ と計算できるのだが、今回は $q_L = 1, : q_R = \exp{(\vec{n} \theta)}$ とすれば事足りる。これは全ての点を原点中心に θ だけ回転移動させていて(3次元回転には無い性質)、北極 p = 1 は $p' = \exp{(\vec{n} \theta)}$ へ移る。4次元回転についての詳細は、成り行きで以前の記事にまとめてあるので、興味があれば見ていただきたい。
以下では簡単なものから扱うために正多胞体の順番を入れ替えている。
正十六胞体
四元数で頂点を表せば p = ±1, ±i, ±j, ±k となる。この通りに直接列挙したほうが楽だが、後のために四元数の積で表しておく。
p = q_1^{m_1} q_2^{m_2} q_3^{m_3} \\
\left\{
\begin{array}{ll}
q_1 = -1, & 0 \le m_1 < 2 \\
q_2 = i, & 0 \le m_2 < 2 \\
q_3 = j, & 0 \le m_3 < 2
\end{array}
\right. \\
\left( q_1 = q_2^2 = q_3^2 = -1 \right)
回転コピーという考え方で説明すると、
- まずは p = 1 の1点だけ用意する
- $q_1$ を使った180°の回転コピーによって p = -1 を作る。合計で p = ±1 の2点となる
- $q_2$ を使った90°の回転コピーによって p = ±i を作る。合計で p = ±1, ±i の4点となり、正方形の頂点を表す
- $q_3$ を使った別方向への90°の回転コピーによって p = ±j, ±k を作る。合計で冒頭の8点となる
正二十四胞体
頂点が24個なので、正十六胞体3つで作れることが期待できる。実際その通りで、正十六胞体の頂点を特定の方向に60°ずつ回転コピーすればいい。
p = q_1^{m_1} q_2^{m_2} q_3^{m_3} q_4^{m_4} \\
\left\{
\begin{array}{ll}
q_1 = -1, & 0 \le m_1 < 2 \\
q_2 = i, & 0 \le m_2 < 2 \\
q_3 = j, & 0 \le m_3 < 2 \\
q_4 = \tfrac{1}{2}+\tfrac{1}{2}i+\tfrac{1}{2}j+\tfrac{1}{2}k, & 0 \le m_4 < 3
\end{array}
\right. \\
\left( q_1 = q_2^2 = q_3^2 = q_4^3 = -1 \right)
正八胞体
単純に考えれば、正二十四胞体の頂点から正十六胞体の分を取り除けばいい。そのためには上の数式で $1 \le m_4 < 3$ とするか、サンプルコードで vertices[8...24] と抜き出す。こうしてできる座標は p = (±1±i±j±k)/2 となっている。
もし1点を北極 p = 1 に配置したければ、適切な四元数を掛けて回転させればいい。その際に $q_4^{-1}$ を選ぶと $q_4^{m_4}$ の指数をひとつ打ち消すことになるので、実は最初から $0 \le m_4 < 2$ とすれば良かったことが分かる。サンプルコードで vertices[0...16] と抜き出しているのも同じ理由。
なお頂点の数16は600の約数でないため、正八胞体を回転コピーして過不足なく複雑化させることはできない。なので正八胞体はもう使わない。
正六百胞体
正二十四胞体の頂点を36°ずつ回転コピーして5倍に増やす。
p = q_1^{m_1} q_2^{m_2} q_3^{m_3} q_4^{m_4} q_5^{m_5} \\
\left\{
\begin{array}{ll}
q_1 = -1, & 0 \le m_1 < 2 \\
q_2 = i, & 0 \le m_2 < 2 \\
q_3 = j, & 0 \le m_3 < 2 \\
q_4 = \tfrac{1}{2}+\tfrac{1}{2}i+\tfrac{1}{2}j+\tfrac{1}{2}k, & 0 \le m_4 < 3 \\
q_5 = \tfrac{\phi}{2}+\tfrac{1}{2}i+\tfrac{\phi^{-1}}{2}j, & 0 \le m_5 < 5
\end{array}
\right. \\
\left( q_1 = q_2^2 = q_3^2 = q_4^3 = q_5^5 = -1 \right)
正五胞体
こればかりは楽する方法が無さそうなので直接列挙しておく。
\begin{align}
p_a &= 1 \\
p_b &= \left( -1 -\sqrt{5}i -\sqrt{5}j -\sqrt{5}k \right) / 4 \\
p_c &= \left( -1 -\sqrt{5}i +\sqrt{5}j +\sqrt{5}k \right) / 4 \\
p_d &= \left( -1 +\sqrt{5}i -\sqrt{5}j +\sqrt{5}k \right) / 4 \\
p_e &= \left( -1 +\sqrt{5}i +\sqrt{5}j -\sqrt{5}k \right) / 4 \\
\end{align}
正百二十胞体
正五胞体を120個、または正六百胞体を5個で作れる。前節までに作った四元数がうまく嚙み合っていれば、単に互いを掛け合わせるだけでいい。ただし掛ける順序は重要で、本記事の値だと正五胞体の座標を右から掛ける必要がある。
正五胞体の頂点が分かっていない場合は、正六百胞体との双対関係を利用して、正六百胞体の胞の中心(正四面体の頂点座標の平均)を求めればいい。胞を構成する頂点の組の求め方は以降で改めて説明する。
双対関係から求めた頂点の四元数は大きさが1より小さくなっているため、他のものと同様に頂点のひとつを北極に持ってきたければ回転と拡大の必要がある。とはいえ方法は簡単で、頂点の四元数をひとつ選んでその逆数を全体に掛ければいい。
辺・面・胞
立体を図に描こうとすれば、頂点の位置だけ分かっていても不十分で、辺や面などの情報を得る必要がある。これも四元数で割と簡単に求められる。
辺・面・胞は、それらを構成する頂点の組が求まればいい。頂点同士の相対的な位置関係は回転後も変わらないので、頂点 p = 1 に対する位置だけ調べておいて各頂点へ回転させることで求まる。つまり、例えば p = 1 を含む $(1, p_s, p_t)$ の3つの頂点で表される要素があれば、p = p' を含む要素のひとつは $(p', p_s p', p_t p')$ の3つの頂点で表される。
ただしこの手法を使うには「任意の2つの頂点座標を掛けた結果もまた頂点である」必要があり、それを満たす正多胞体は正十六胞体・正二十四胞体・正六百胞体だけである。残りの正多胞体は双対関係を利用するなど他の方法が必要になる。
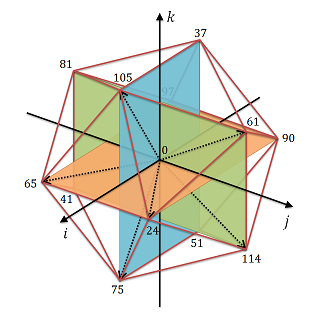
全部の正多胞体について考えるのは大変なので、ここでは正六百胞体だけを扱う。正六百胞体ではどの頂点も12個の隣がいて、それらは正二十面体の頂点のような配置になっている。頂点 p = 1 に対する隣の頂点は、実部が φ/2 の四元数である。その配置を図にすると以下のようになる(数字はサンプルコードの配列の添字)。
p = 1 (添字0)を含む要素は、辺が12本・面が30枚・胞が20個ある。ただしこれらをそのまま全ての他の頂点 p' へ回転させると重複が出るので、事前に重複を防ぐなら図で点線矢印が伸びている頂点 {24, 65, 105, 61, 114, 75} のみ使うといい。その場合は辺が6本・面が10枚・胞が5個となり、120倍するときちんと正六百胞体の要素の数に一致する。