賞金総額100万円のハッカソン開催
フィックスターズが賞金総額100万円のハッカソンを2021年3月に開催。サービスリリースした直後でユーザーが少ないので、使い慣れている玄人はほとんど居ないはず。
https://amplify.fixstars.com/hackathon00

玄人が居ないのであれば、アイデア次第で初心者でもワンチャンスあるかも?
最優秀賞で40万円。これは熱い。
前回まで
episode 0、初期設定編
https://qiita.com/HIROTTA-MAN/items/111e7733a3a8b3b6870d
episode 1、数独編その1
https://qiita.com/HIROTTA-MAN/items/a94fb38d95cb186ef54b
はじめに
このコンテンツは、ハッカソンの開催をきっかけに量子アニーリングのプログラミングを体験してみる企画です。使うイジングマシン「Amplify AE」は量子コンピュータではありませんが、同じソースコードが使えるので、実質的に量子プログラミングの勉強をしているはず。
数独を解いてみよう
とりあえず、まずは恒例のイジングマシンの設定。今回も環境はJupyterLabです。
from amplify.client import FixstarsClient
client = FixstarsClient()
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"
client.parameters.timeout = 1000 # 1 sec
※アクセストークンは公開しないように。XXXXXの部分は各自で書き換えてください。
前回のおさらい
前回は数独を解く上で必要な、二値変数の組合せ最適化で1~9までの選択肢を最適化する手法を学びました。
9個の変数$q_i (i=0 \sim 8)$をセットにして1~9の数字を表します。この時、必要なのが、$q_i$は一つだけ1を取るというone-hot制約を使うことです。この制約の設定には、関数equal_toを使いました。
from amplify import (
BinaryQuadraticModel,
Solver,
BinaryPoly,
gen_symbols,
decode_solution
)
from amplify.constraint import equal_to
q = gen_symbols(BinaryPoly,9)
f = equal_to(sum(q),1)
model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)
q_result = decode_solution(q, result[0].values)
print(q_result)
print("number is ", q_result.index(1) + 1)
ところで、イジングマシンは評価関数の値が最も小さくなる組み合わせを探す計算機です。上のコードでは、一体なにが小さくなるように組み合わせを探したのでしょうか。fは等式の形なので、「値が小さくなる組み合わせ」といった変化が入る余地はありません。
QUBO模型と制約条件
0か1かで組合せ最適化問題を解くイジングマシンが扱うのは、QUBO模型と呼ばれる数理模型です。QUBOとは
- Quadratic 二次形式
- Unconstrained 制約なし
- Binary 二値変数
- Optimization 最適化
の略です。名前に「制約なし」とあるように、イジングマシン(QUBO模型)では制約条件を直接扱えません。
ドキュメントによると、Fixstars Amplifyではこの制約条件を自動で変換してQUBO模型に反映しているようです。例えば、one-hot制約と同等の結果は次のような評価関数でも得られます。
$$
f = \left(\sum_{i=0}^N q_i -1 \right) ^2
$$
QUBO模型では、制約条件を「絶対に守る条件」ではなく、「守ったほうが評価関数の値が小さくなる」ようにして評価関数に加え、間接的に適用します。Fixstars Amplifyではこうした典型的な制約条件についてequal_toのようなヘルパー関数を用意していて、実行時に自動で変換してくれているようです。なんて素人に優しい仕様。
参照:ヘルパー関数を用いた構築 ― Amplify SDK ドキュメント
9x9マスに数字を並べる
まずは、前回1行9マスに重複なく数字を並べた延長線として、9x9マスに行・列の重複なく数字を並べてみます。まずは完成形から。
from amplify import (
BinaryQuadraticModel,
Solver,
BinaryPoly,
gen_symbols,
decode_solution
)
from amplify.constraint import equal_to
q = gen_symbols(BinaryPoly,9,9,9)
f1 = [equal_to(sum([q[i][j][k] for i in range(9)]),1) for j in range(9) for k in range(9)]
f2 = [equal_to(sum([q[i][j][k] for j in range(9)]),1) for i in range(9) for k in range(9)]
f3 = [equal_to(sum([q[i][j][k] for k in range(9)]),1) for i in range(9) for j in range(9)]
f = sum(f1)+sum(f2)+sum(f3)
model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)
q_result = decode_solution(q, result[0].values)
for i in q_result:
print([j.index(1) +1 for j in i])
リスト内包表記
リスト内包表記が苦手な人がいるかもしれないので、少しだけ説明を追加しておきます。
$q_{i j k}$は、$i+1$行$j+1$列目に値$k+1$が入るか入らないかを示しています。インデックス番号は0から数えるので$+1$しています。
もしq[3][5][6]の値が1だったら、4行6列目のマスには7が入ります。
それでは、次の制約条件を一つずつ分解してみてみましょう。
f1 = [equal_to(sum([q[i][j][k] for i in range(9)]),1) for j in range(9) for k in range(9)]
[q[i][j][k] for i inrage(9)]はiがrange(9)で変化するので、$[q_{0 jk}, q_{1 jk}, q_{2 jk}, q_{3 jk}, q_{4 jk}, q_{5 jk}, q_{6 jk}, q_{7 jk}, q_{8 jk}]$という配列を表しています。列($j$)と値($k$)を一定にしたまま、行($i$)を変化させた集合です。
sum([q[i][j][k] for i in range(9)])とあるので、j・kを一定にしたまま各行の変数を合計しています。
equal_to(sum([q[i][j][k] for i in range(9)]),1)とあるので、合計した値が1になるように制約条件を設定しています。合計しているのは$j+1$列の各マスに値$k+1$が入るかどうかを表して二値変数なので、「列$j+1$には値$k+1$が1つだけ入る」という制約を課しています。
for j in range(9) for k in range(9)は、この関数equal_toを各列($j$)、各値($k$)で同様に適用し、それぞれで制約を課しています。
同様に、f2は「行$i+1$には値$k+1$が一つだけ入る」を、f3は「行$i+1$・列$j+1$には値が一つだけ入る」というという制約を設定しています。
さて、各行・各列それぞれで数字の重複がないようにマスを埋められましたが、数独の答えにはなっていません。3x3のマス内でも数字が重複しないように、もう一つ制約を加えます。
3x3マスに制約条件を設定する
ここでのテクニックは「イジングマシンの」というより「Pythonの」ものでしょう。演算記号をうまいこと使って、リスト内包表記で3x3マスをうまく表現します。
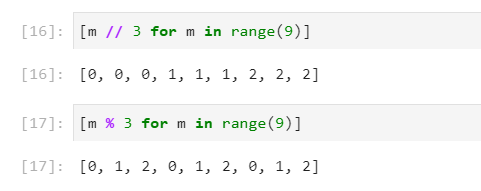
使うのは、切り捨て除算(//)と、Mod関数などとも呼ばれる剰余演算(%)です。
組み合わせると、ちょうど3x3マスのインデックス番号を表現できます。
これを9ヶ所の各3x3マスで、各値$k$に対するone-hot制約を課します。
これで、数独の全ての制約条件を設定できました。
答えを求め、出力を見てみます。
from amplify import (
BinaryQuadraticModel,
Solver,
BinaryPoly,
gen_symbols,
decode_solution
)
from amplify.constraint import equal_to
q = gen_symbols(BinaryPoly,9,9,9)
f1 = [equal_to(sum([q[i][j][k] for i in range(9)]),1) for j in range(9) for k in range(9)]
f2 = [equal_to(sum([q[i][j][k] for j in range(9)]),1) for i in range(9) for k in range(9)]
f3 = [equal_to(sum([q[i][j][k] for k in range(9)]),1) for i in range(9) for j in range(9)]
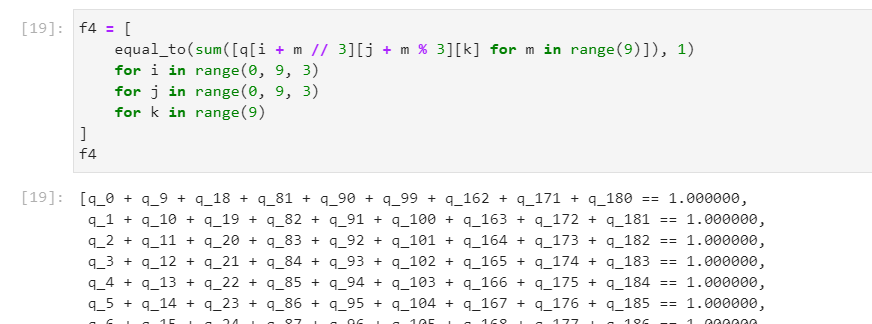
f4 = [
equal_to(sum([q[i + m // 3][j + m % 3][k] for m in range(9)]), 1)
for i in range(0, 9, 3)
for j in range(0, 9, 3)
for k in range(9)
]
f = sum(f1)+sum(f2)+sum(f3)+sum(f4)
model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)
q_result = decode_solution(q, result[0].values)
for i in q_result:
print([j.index(1) +1 for j in i])
きちんと3x3マスでも数字の重複がありません。
出力の調整
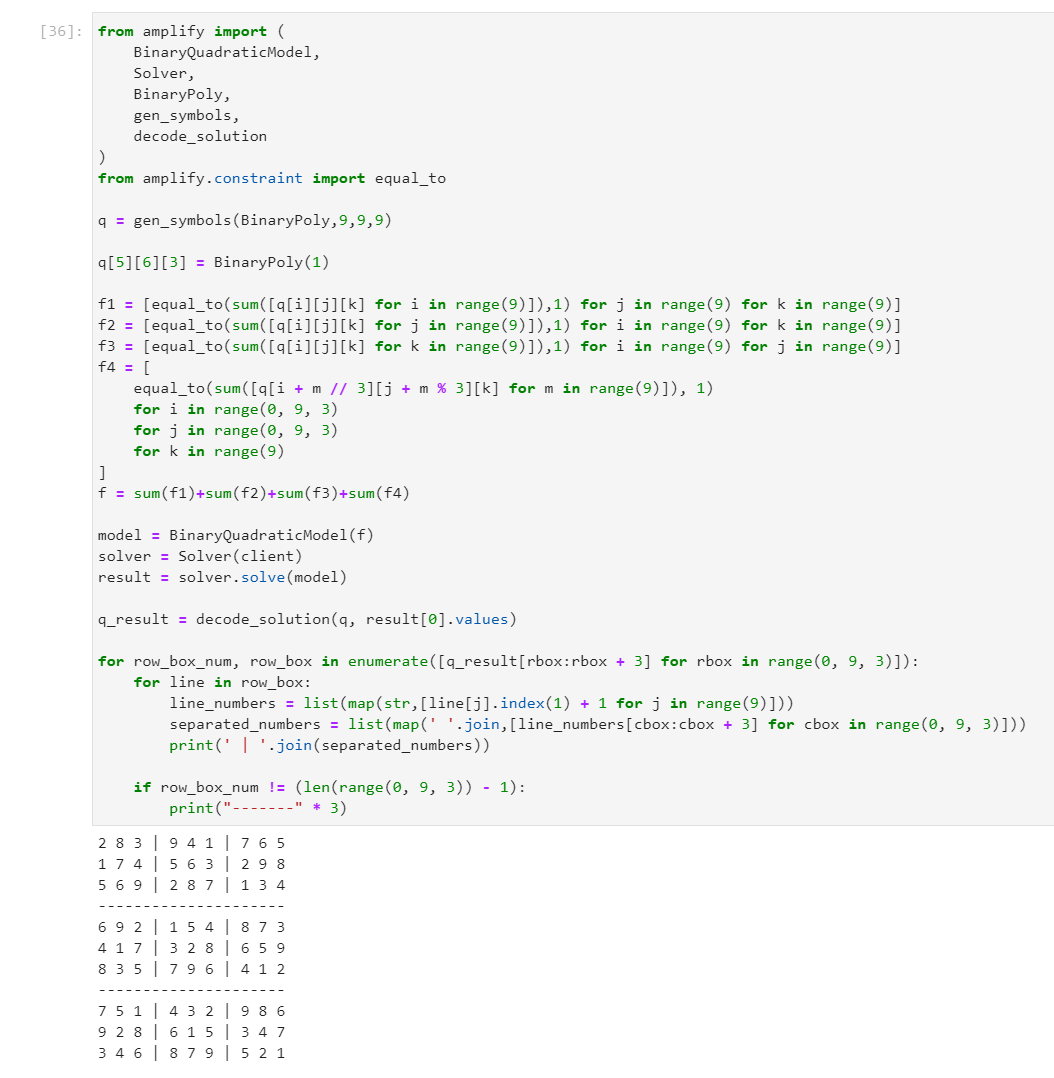
せっかくなので、出力も数独っぽく調整してみましょう。
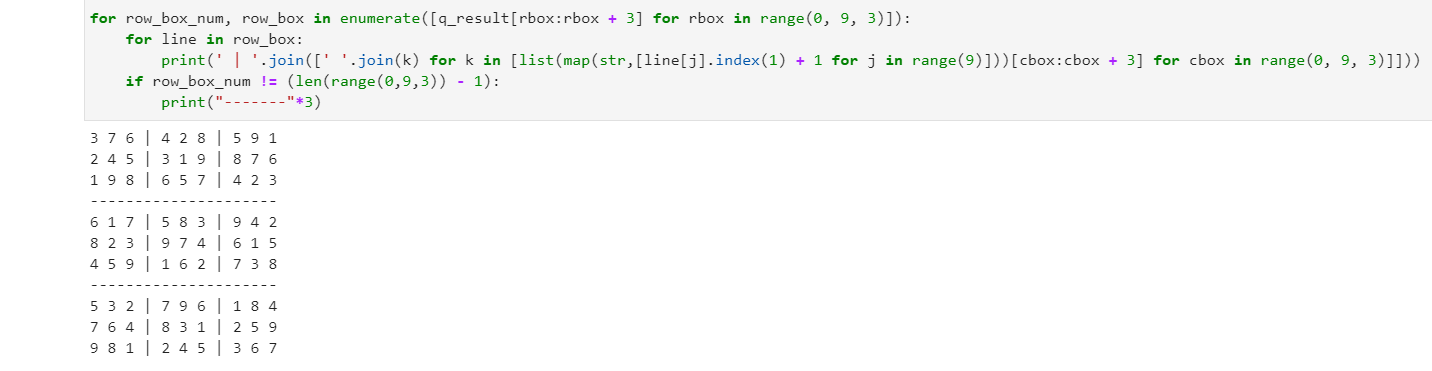
for row_box_num, row_box in enumerate([q_result[rbox:rbox + 3] for rbox in range(0, 9, 3)]):
for line in row_box:
print(' | '.join([' '.join(k) for k in [list(map(str,[line[j].index(1) + 1 for j in range(9)]))[cbox:cbox + 3] for cbox in range(0, 9, 3)]]))
if row_box_num != (len(range(0,9,3)) - 1):
print("-------"*3)
おっと、ワンライナーの悪い癖が出ましたね。joinメソッドを使いたくて、1行の出力を1行の処理で書いてしまいました。
本題ではないので、特に説明せずに表記を少し整えるだけして次に行きたいとおもいます。
from amplify import (
BinaryQuadraticModel,
Solver,
BinaryPoly,
gen_symbols,
decode_solution
)
from amplify.constraint import equal_to
q = gen_symbols(BinaryPoly,9,9,9)
f1 = [equal_to(sum([q[i][j][k] for i in range(9)]),1) for j in range(9) for k in range(9)]
f2 = [equal_to(sum([q[i][j][k] for j in range(9)]),1) for i in range(9) for k in range(9)]
f3 = [equal_to(sum([q[i][j][k] for k in range(9)]),1) for i in range(9) for j in range(9)]
f4 = [
equal_to(sum([q[i + m // 3][j + m % 3][k] for m in range(9)]), 1)
for i in range(0, 9, 3)
for j in range(0, 9, 3)
for k in range(9)
]
f = sum(f1)+sum(f2)+sum(f3)+sum(f4)
model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)
q_result = decode_solution(q, result[0].values)
for row_box_num, row_box in enumerate([q_result[rbox:rbox + 3] for rbox in range(0, 9, 3)]):
for line in row_box:
line_numbers = list(map(str,[line[j].index(1) + 1 for j in range(9)]))
separated_numbers = list(map(' '.join,[line_numbers[cbox:cbox + 3] for cbox in range(0, 9, 3)]))
print(' | '.join(separated_numbers))
if row_box_num != (len(range(0, 9, 3)) - 1):
print("-------" * 3)
初期値を入れて問題を解く
数独の条件を満たした出力は得られましたが、これでは数独の答えではありません。なにせ問題を入力していないのです。だから出力は計算するたびに結果が変わってしまいます。
数独の問題は、いくつかのマスだけ最初から埋まっています。これによって答えが一つに定まるのです。
では、このプログラムでも初期値を設定してみましょう。
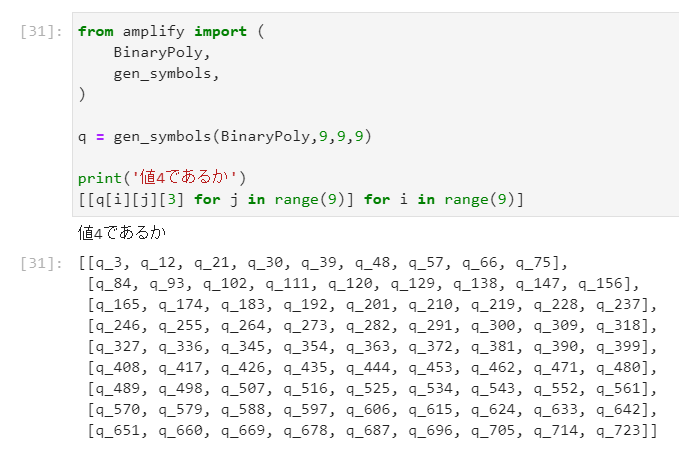
関数gen_symbolsで二値変数の配列を作った時、全ての変数は0か1か定まっていません。例えば各行・列に値4が入るかどうかを示す9x9個の二値変数は、いずれもq_numで表現されています。
では、6行目・7列目の初期値を4だと定めてみましょう。インデックス番号は0から始まるので、行・列の値と1つずれます。二値変数q[5][6][3]の値を、BinaryPoly型の1だと設定します。
q[5][6][3] = BinaryPoly(1)
一覧の中に、一つだけ「1」と表示されています。これで初期値が設定できました。
このまま数独の答えを求めると、少なくとも6行目・7列目のマスは必ず4になるはずです。
同様に、問題で定められている初期値を入力すれば答えが解けます。
それでは、次の問題を解いてみます。
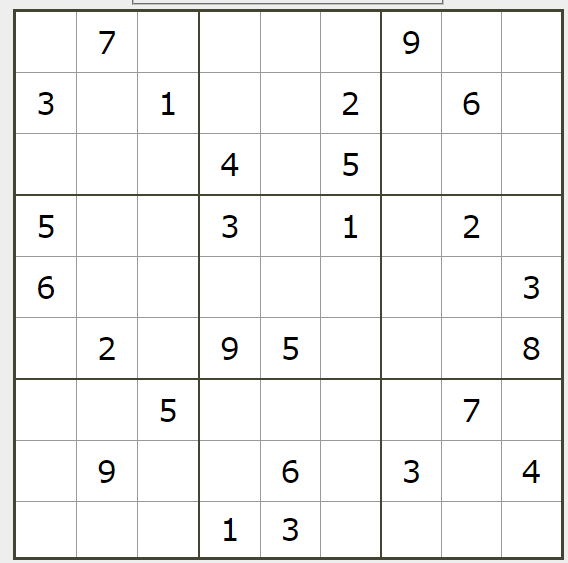
参照:http://www.sudokugame.org/archive/printable.php?nd=4&y=2021&m=02&d=23
初期値はnumpyの配列で作りました。空欄は0にして値を入れてあります。
import numpy as np
initial = np.array([
[0, 7, 0, 0, 0, 0, 9, 0, 0],
[3, 0, 1, 0, 0, 2, 0, 6, 0],
[0, 0, 0, 4, 0, 5, 0, 0, 0],
[5, 0, 0, 3, 0, 1, 0, 2, 0],
[6, 0, 0, 0, 0, 0, 0, 0, 3],
[0, 2, 0, 9, 5, 0, 0, 0, 8],
[0, 0, 5, 0, 0, 0, 0, 7, 0],
[0, 9, 0, 0, 6, 0, 3, 0, 4],
[0, 0, 0, 1, 3, 0, 0, 0, 0],
])
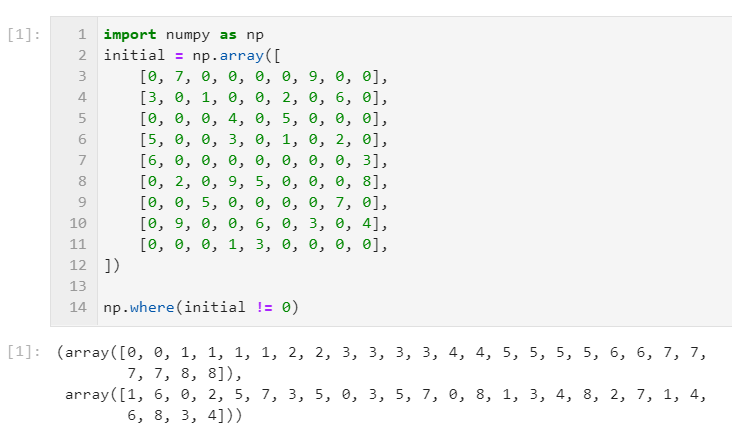
値が0でないマス目は、関数np.whereで得られます。
np.where(initial != 0)
出力はインデックス番号の配列です。initialは二重配列なので、得られるインデックス番号の配列2つはそれぞれ行インデックスと列インデックスに対応します。
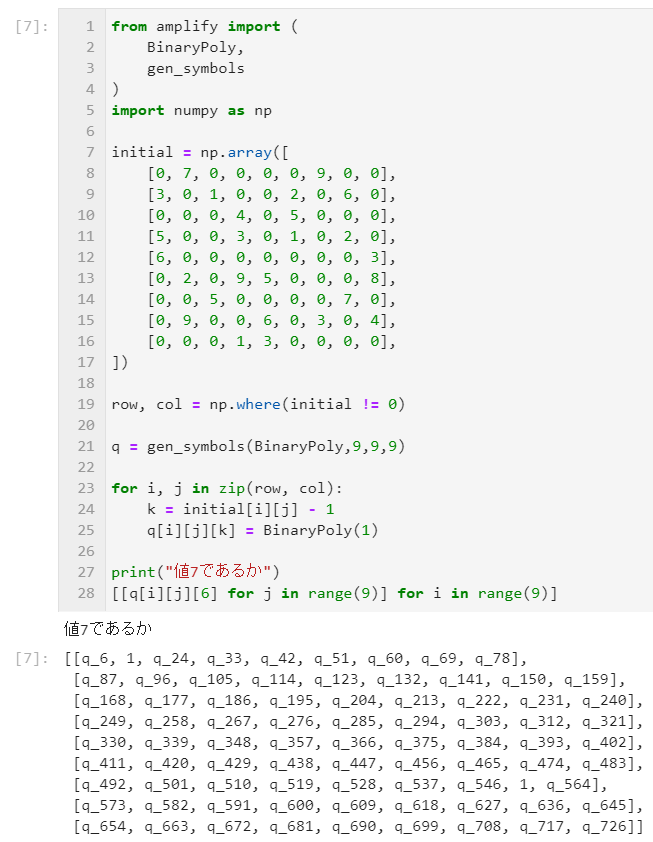
これを使って、初期値が決まっているq[i][j][k]にBinaryPoly(1)を入れていきます。
row, col = np.where(initial != 0)
q = gen_symbols(BinaryPoly,9,9,9)
for i, j in zip(row, col):
k = initial[i][j] - 1
q[i][j][k] = BinaryPoly(1)
ちゃんと初期値7のマスに対応する二値変数qが1になっています。これでイジングマシンを動かせば、答えが得られます。
関数化するよ
とりあえず問題は解けましたが、このままだと取り回しが悪いので関数化します。
完成形がこちら。
from amplify import (
BinaryQuadraticModel,
Solver,
BinaryPoly,
gen_symbols,
decode_solution
)
from amplify.constraint import equal_to
import numpy as np
from math import sqrt
def sudoku_output(matrix :list):
width = len(matrix)
boxes = int(sqrt(width))
for row_box_num, row_box in enumerate([matrix[rbox:rbox + boxes] for rbox in range(0, width, boxes)]):
for line in row_box:
line_numbers = list(map(lambda x: str(x).rjust(len(str(width))),line))
separated_numbers = list(map(' '.join,[line_numbers[cbox:cbox + boxes] for cbox in range(0, width, boxes)]))
print(' | '.join(separated_numbers))
if row_box_num != (len(range(0, width, boxes)) - 1):
print("-" * (boxes * (len(str(width)) +1) * boxes + 2 * (boxes - 1)))
def sudoku_solve(matrix :np.ndarray):
width = len(matrix)
boxes = int(sqrt(width))
q = gen_symbols(BinaryPoly, width, width, width)
if matrix.any():
row, col = np.where(matrix != 0)
for i, j in zip(row, col):
k = matrix[i][j] - 1
q[i][j][k] = BinaryPoly(1)
f1 = [equal_to(sum([q[i][j][k] for i in range(width)]),1) for j in range(width) for k in range(width)]
f2 = [equal_to(sum([q[i][j][k] for j in range(width)]),1) for i in range(width) for k in range(width)]
f3 = [equal_to(sum([q[i][j][k] for k in range(width)]),1) for i in range(width) for j in range(width)]
f4 = [
equal_to(sum([q[i + m // boxes][j + m % boxes][k] for m in range(width)]), 1)
for i in range(0, width, boxes)
for j in range(0, width, boxes)
for k in range(width)
]
f = sum(f1)+sum(f2)+sum(f3)+sum(f4)
model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)
q_result = decode_solution(q, result[0].values)
return [[q_result[i][j].index(1) + 1 for j in range(width)] for i in range(width)]
if __name__ == "__main__":
initial = np.array([
[0, 7, 0, 0, 0, 0, 9, 0, 0],
[3, 0, 1, 0, 0, 2, 0, 6, 0],
[0, 0, 0, 4, 0, 5, 0, 0, 0],
[5, 0, 0, 3, 0, 1, 0, 2, 0],
[6, 0, 0, 0, 0, 0, 0, 0, 3],
[0, 2, 0, 9, 5, 0, 0, 0, 8],
[0, 0, 5, 0, 0, 0, 0, 7, 0],
[0, 9, 0, 0, 6, 0, 3, 0, 4],
[0, 0, 0, 1, 3, 0, 0, 0, 0],
])
print('initial')
sudoku_output(initial.tolist())
print()
print('solved')
result = sudoku_solve(initial)
sudoku_output(result)
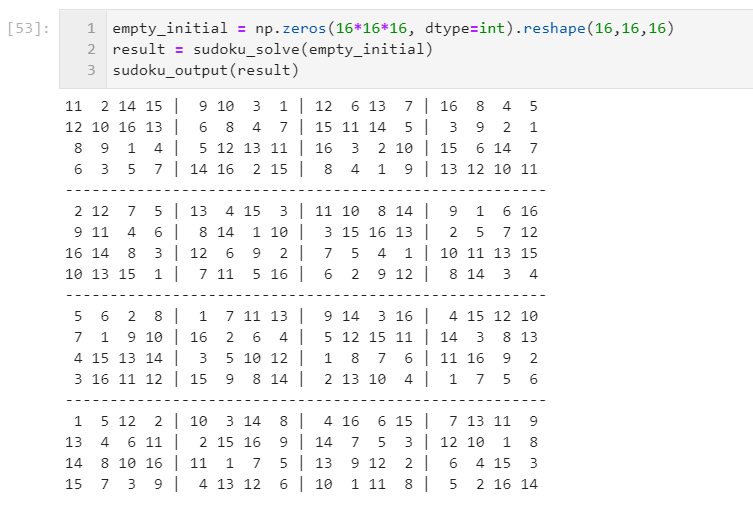
もっと広いマス数に拡張
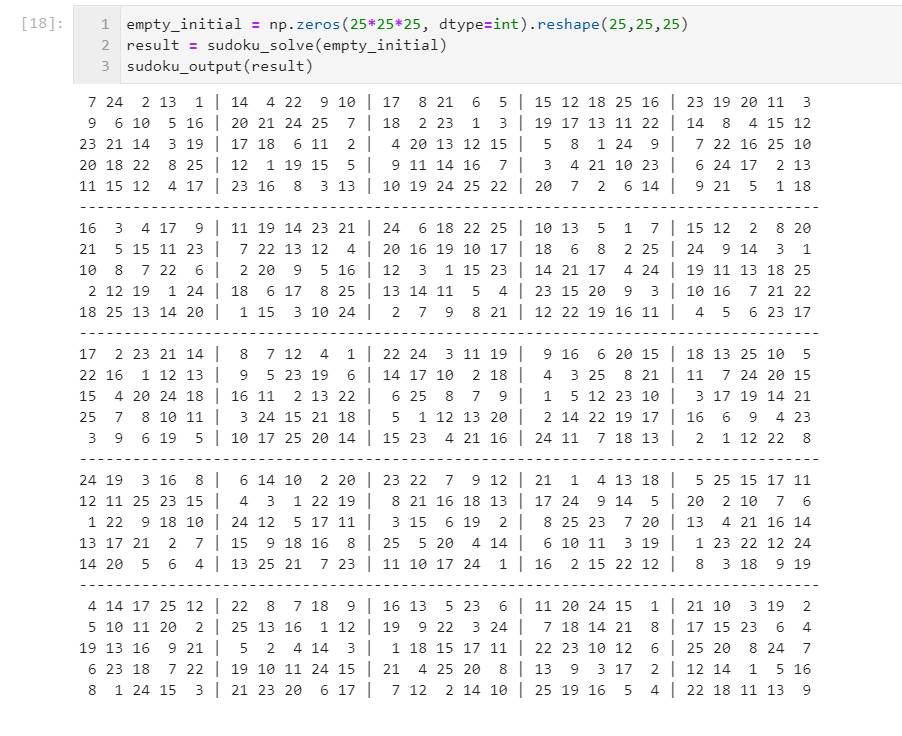
ところどころにwidthとかboxesとかに書き換えているのは、数独を拡張するため。例えば、16x16マスもこのコードなら解けます。
25x25もなんとか。
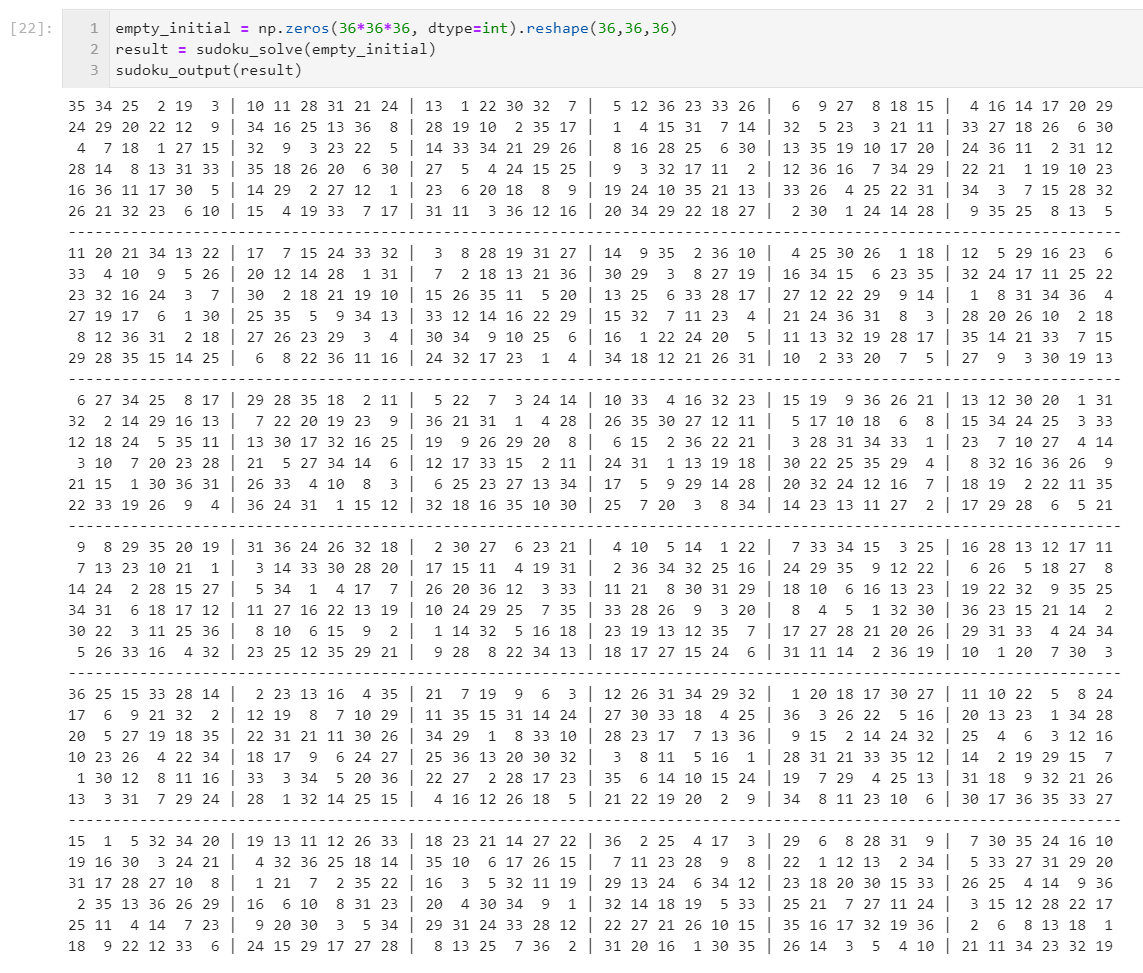
36x36はタイムアウトを10秒に設定したらいけました。これぐらいになると、制約条件を設定しているPython上のループ処理が重たい。
おしまい
というわけで、チュートリアルの数独をやっていきました。
基本はドキュメントに書いてある内容だけど、部分的に自分好みに書き換えています。複雑な所はSDKが自動化してくれているし、それほど難しくはなかったのでは?
参照:Sudoku ― Amplify SDK ドキュメント
次回は数独で勉強したことを応用して、チュートリアルにはない魔方陣に挑戦してみようかな。
Fixstars Amplify ハッカソン
前回まで
episode 0、初期設定編
https://qiita.com/HIROTTA-MAN/items/111e7733a3a8b3b6870d
episode 1、数独編その1
https://qiita.com/HIROTTA-MAN/items/a94fb38d95cb186ef54b