More than 3 years have passed since last update.

賞金総額100万円目指して0から量子プログラミング　episode 1、数独編その1

Last updated at 2021-02-23Posted at 2021-02-21

賞金総額100万円のハッカソン開催

フィックスターズが賞金総額100万円のハッカソンを2021年3月に開催。サービスリリースした直後でユーザーが少ないので、使い慣れている玄人はほとんど居ないはず。
https://amplify.fixstars.com/hackathon00

玄人が居ないのであれば、アイデア次第で初心者でもワンチャンスあるかも？
最優秀賞で40万円。これは熱い。

前回

episode 0、初期設定編
https://qiita.com/HIROTTA-MAN/items/111e7733a3a8b3b6870d

はじめに

このコンテンツは、ハッカソンの開催をきっかけに量子アニーリングのプログラミングを体験してみる企画です。使うイジングマシン「Amplify AE」は量子コンピュータではありませんが、同じソースコードが使えるので、実質的に量子プログラミングの勉強をしているはず。

数独を解いてみよう

チュートリアルにあったので数独を解いています。縦と横、3x3の太枠内でそれぞれ1～9を重複なく使うようにマスを埋めるペンシルパズル。ナンプレ（ナンバープレース）とも。

とりあえず、まずはイジングマシンの設定。今回も環境はJupyterLabです。


from amplify.client import FixstarsClient

client = FixstarsClient()
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"
client.parameters.timeout = 1000  # 1 sec

※アクセストークンは公開しないように。XXXXXの部分は各自で書き換えてください。

二値変数しか扱えない組合せ最適化で数独

量子アニーリングは量子ビットが上か下に落ち着く現象を使っているので、基本的に扱える変数は二択です。でも、解きたい数独で扱うのは1～9の選択肢。

まずは二値変数で2より大きい選択肢を扱う方法を見ていきます。

アイデアは単純で、各二値変数を「Ture/False」として扱い、例えば「1であるか」という問いに$q_0$を。「2であるか」には$q_1$をと対応させてる方法。いわゆるone-hot制約を使い、9個の二値変数をまとめて9択の変数のように使います。

たとえば、9個の二値変数$q_i$($i=0$～$8$）を使って7を表すと、下のような True/False の組み合わせ。

	$q_i$	True(1)/False(0)
1である	$q_0$	0
2である	$q_1$	0
3である	$q_2$	0
4である	$q_3$	0
5である	$q_4$	0
6である	$q_5$	0
7である	$q_6$	1
8である	$q_7$	0
9である	$q_8$	0

equal_to

こうして1～9の選択肢を表現する上で必要なのは、「$q_i$はどれか一つだけが1になる」という制約条件です。これが守られないと、「3であると同時に9でもある」みたいな答えになってしまう。

こうした制約条件を設定するための関数もAmplify SDKには用意されています。one-hot制約は、関数equal_toを使えばとても簡単にかけます。

from amplify import BinaryPoly, gen_symbols
from amplify.constraint import equal_to

q = gen_symbols(BinaryPoly,9)
f = equal_to(sum(q),1)

print(q)
print(f)

0か1の二値変数を全て足した値が1に等しければ、one-hot制約として成り立つでしょう。

せっかくJupyter環境を使っているので、数式っぽい出力もしておきます。

ちゃんと制約条件が適用されるか、one-hot制約だけで計算してみます。

from amplify import BinaryQuadraticModel, Solver
from amplify import BinaryPoly, gen_symbols
from amplify.constraint import equal_to

q = gen_symbols(BinaryPoly,9)
f = equal_to(sum(q),1)

model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)

result[0].values

$q_8$だけが1で、ほかは全て0になっています。1～9の選択肢に割り当てると、9という答えが得られたということですね。

計算条件にはone-hot制約しか設定していないので、このコードは計算するたびにどの値になるか変わります。

decode_solution

このままでも良いのですが、処理結果が見づらいのでdecode_solutionも使いましょう。

decode_solution(変数配列、処理結果)を使うと、割り当て直して答えが得られます。q_8に対応する9番目の処理結果が1で、ほかが0なのが読み取りやすいですね。

まとめるとこんなコードに。

from amplify import BinaryQuadraticModel, Solver
from amplify import BinaryPoly, gen_symbols, decode_solution
from amplify.constraint import equal_to

q = gen_symbols(BinaryPoly,9)
f = equal_to(sum(q),1)

model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)

q_result = decode_solution(q, result[0].values)

print(q_result)
print("number is ",q_result.index(1) + 1)

インデックス番号$i$は割り当てた数字と1ずれているので、q_result.index(1) + 1と1を足しています。この時は、6という結果が得られました。

1行に並ぶ1～9

数独はequal_toだけで解けます。順番にすこしずつやっていきましょう。
まずは1～9の数字が入るマスを1行・9マスだけ考えてみましょう。

二値変数の配列を作るgen_symbolsは、引数を増やすことで多次配列も作れます。

qは9$\times$9の二重配列になっています。これを使って、9マスの数字を考えるわけです。各9マスに9個ずつ二値配列を割り当てて使います。分かりやすく出力するとこんな感じ？

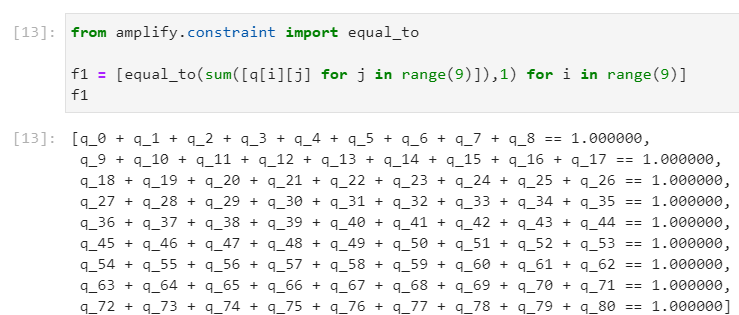
まずは、各マスが1～9のどれかになるように制約条件を設定します。$q_{ij}$で表すと、$j$が値1～9を表し、$i$が1マス目～9マス目を表しています。

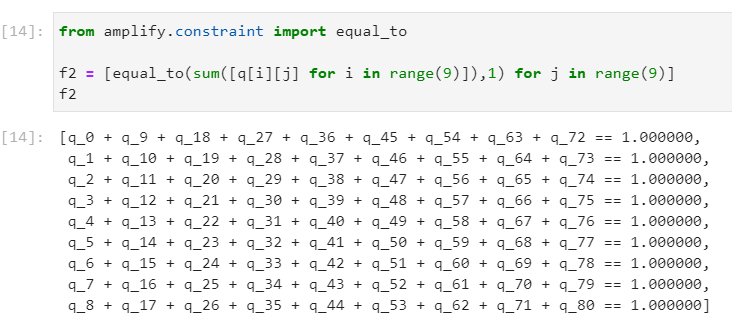
次は、マスに入る値が重複しないように制約条件を設定します。今回は9つのマスに9つの数字を入れていくので、各値（$j$）はどこかのマス（$i$）に1度だけ入ります。

制約条件が記述できたら、計算してみます。
計算するときは、f1とf2を足して一つにしておきます。

from amplify import BinaryQuadraticModel, Solver
from amplify import BinaryPoly, gen_symbols, decode_solution
from amplify.constraint import equal_to
import numpy as np

q = gen_symbols(BinaryPoly,9,9)
f1 = [equal_to(sum([q[i][j] for j in range(9)]),1) for i in range(9)]
f2 = [equal_to(sum([q[i][j] for i in range(9)]),1) for j in range(9)]
f = sum(f1)+sum(f2)

model = BinaryQuadraticModel(f)
solver = Solver(client)
result = solver.solve(model)

q_result = decode_solution(q, result[0].values)

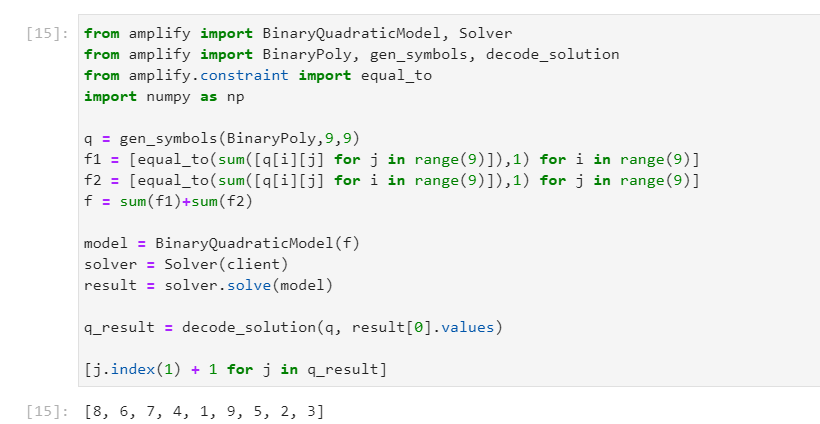
[j.index(1) + 1 for j in q_result]

無事、1行の重複のない数字が得られました。この答えも$9! = 362880$通りあるので、実行するたびに得られる値は変わります。

と、重複しない数字の組み合わせを求める制約条件の使い方がなんとなくわかった所で続きは次回。

数独編その2では、いよいよ9行9列が解けます！

Fixstars Amplify ハッカソン

前回