とりあえず見て触れて!
最大正方形の面積探索をビジュアライズしたWEBページを作成しました!
はじめに
上記のWEBページは最大正方形の面積を動的計画法(DP)によって探索する際の動きをビジュアライズ化したものです。
具体的にどういうものを解いてるのかというと以下のような問題です。
AIZU ONLINE JUDGE-Largest Square
この問題について、DPを用いると $O(HW)$ で解くことができます。
$HW$のステップ数で最大正方形を導き出せていることが分かると思います。
初歩的なことからゆるーく説明していくので、なんとなーくでいいので知識や理解が深まれば嬉しいです。
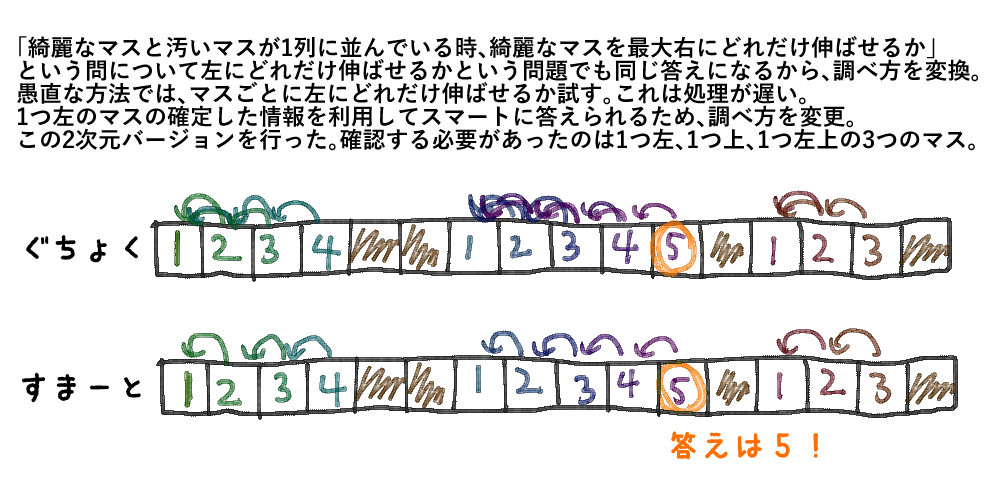
最大正方形はどのようにして求まるか
愚直に最大正方形を求めようとすると、それぞれのマスを起点に、辺が $1$ の正方形を作れるか、辺が $2$ の正方形を作れるか…のように調べると思います。
これでは辺が $N$ の正方形が出来るか調べる場合、マスごとに $N^2$ のマス全てを確認するような動きです。ぶっちゃけ遅いです。
ちょっと思考を変えましょう。
先ほどのイメージだと、起点のマスが左上に来る場合の正方形の辺の大きさを求めていたと思います。
正方形の右下のマスになる場合を考えるとどうでしょうか。この考えであれば、自身の1つ左のマスが作れる正方形の辺の大きさ、1つ上側のマスが作れる正方形の辺の大きさ、1つ左上側のマスが作れる正方形の辺の大きさのうち、一番小さい値に $1$ を足した値が答えとなるのです。

そして、左上から右下に向けて順に確認していけば、1つ上、1つ左、1つ左上のマスの情報は確定しています。
これは、DPで解くことができます。
説明が雑過ぎて分からない方へ
以下の画像から、感覚だけでもつかんでいただければ幸いです。余計に混乱を招くだけだとしたら申し訳なく…
DPとは?
プログラミングを初歩から学べて練習もできる「アルゴ式」の説明がとても分かりやすいため、引用します。
このように、もとの問題を一連の部分問題へと分解し、それぞれの部分問題の解をメモ化しながら、小さな部分問題からより大きな部分問題の解を順に求めていく手法を総称して、動的計画法とよびます。
このとき、より大きな部分問題の解を求めるために、小さな部分問題に対してメモ化された値を再利用していることがポイントとなります。
このようなメモ化はキャッシュとよばれる考え方でもあります。「同じ計算をふたたび行わないようにする」という考え方が根底にあります。
値が確定している結果を使用して、次の結果を求める…を繰り返し、最終的に求めたい答えを導き出すアルゴリズムです。
先ほどの最大正方形の求め方も、値が確定している右、上、左上のマスの情報から最終的に求めたい正方形の辺の長さを求めることが出来ています。
競技プログラミングをちょこっとかじった人は、フィボナッチ数列の例から「DPって足し算のことでしょ。この問題って足し算じゃないじゃん。略して足しじゃん」
と考えちゃうかもしれませんが、足し算であることがDPではありません。途中の結果を再利用して高速化することがDPなのです。
2次元DPは難しい?
1次元DPはなんとなく分かる。けど2次元DPは分からない…という方がいらっしゃいます。
DPについての説明は、2次元DPにもそのまま当てはまっています。
やっていることの本質は1次元DPも2次元DPも差がないです。3次元DPでも4次元DPでも同じことです。
では何が難しいと感じたのか考えれば、単に解こうとした問題が難しかったのだと思います。
その上でよく分からないから理解しようとして読んだ解説の、TeX記法が記号だらけで拒否感が出てしまうのかもしれません。
まずは左、上、左上の情報さえわかればいいような優しい問題から順に慣れていきましょう。
すると解説の説明もなんとなく理解できるようになっていきます。
今回の内容も解説とかであれば、以下みたいな書き方されてますが、何度も書いてる通り、左、上、左上の最小値に $1$ を足したものが答えだよ。と説明しているだけだと思えば少しは親近感が湧かないでしょうか。
$dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1$
だめ? 湧かない? ボクハディーピーダヨ! ミンナトナカヨクシタイヨー! (裏声)
これで親近感が生まれたと思います。
仲良くなったところで、1次元DP、2次元DP併せて慣れるためにお勧めな簡単な問題の紹介です。
- アルゴ式 動的計画法 (DP)
- Atcoder Educational DP Contest / DP まとめコンテスト (A~Eまで、以降は大分むずかしいため…)
以上の問題が解けるようになれば、他の問題も解いていきましょう。
例えば以下の問題です。AtcoderでのDiffは1000以上と難しめの問題です。これが解けるようになれば、2次元DPに慣れたと思って構わないと思います。
難しいDP問題について
上記の説明だけ聞くと、強い人でも解けないDPの問題があるというのが不思議に思えるかもしれません。
ある一定の力があればなんだって解けるような気がしてきます。どこで難易度の差が生まれるのか。
それは遷移がややこしかったり、累積和をとって処理を高速化する必要があったり、遷移に不要な情報を消して次元を落とさないといけなかったり…難しい問題ではなんらかの工夫が必要になってくるのです。こんな記事書いてますが、DP苦手です。
自作の紹介で申し訳ありませんが、工夫が必要になるDP問題を作問したことがあります。
ぱっと見で2次元以上のDPになりそうですが、1次元のDPに情報をまとめることができます。
より難しい問題を解いてみたいなと思った方は是非挑戦してみてください。
貰うDPと配るDP
DPには貰うDPと配るDPがあります。
大半の人からして貰うDPについてイメージが付きやすく、配るDPが何をやっているのかいまいち理解しにくいのではないかと思います。
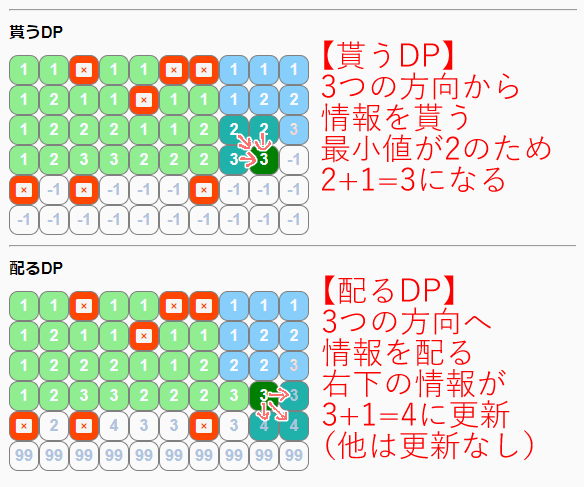
今回紹介している配るDPのアルゴリズムは、面積を求める例では自身のマスの右、下、右下について、自身のマスを右下にして作れる正方形の大きさ $+ 1$の値よりも大きい場合、その値に更新するということを行っていきます。
貰うDPだと3方向から値を取得してくるため、以下のような処理です。
$dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1$
配るDPだと3方向へ値を配っていくため、以下のような処理です。
$dp[i][j+1] = min(dp[i][j+1], dp[i][j] + 1 )$
$dp[i+1][j] = min(dp[i+1][j], dp[i][j] + 1 )$
$dp[i+1][j+1] = min(dp[i+1][j+1], dp[i][j] + 1 )$
自身のマスに来るまでに3方向から都度更新が起こり、自身のマスの処理の時には以下の情報の値になっています。
$+1$ が中に入っているかどうかの違いで、貰うDPと結果は等しいです。
$dp[i][j] = min(dp[i][j-1] + 1, dp[i-1][j] + 1, dp[i-1][j-1] + 1 )$
初期値や求め方のアルゴリズムに異なりがありますが、最終的に求まる結果は一緒になっています。
また、それぞれのステップによって結果が確定している(薄緑になっている)マスの情報も等しいです。
値が確定している情報を利用している点も変わりませんし、結果を求めるのに利用している情報の位置も個数も変わりません。
貰うか配るかのやり方の異なりで、確定している部分の結果に変化が生じることはありません。生じてしまえばどちらかがバグっています。
(仮にビジュアライザで結果が違っていた場合はバグなので叱責してください)
他の例についても知りたいという方がいましたら、「アルゴ式」にて【左上のマスから右下のマスまで最短で至る経路の本数】を求めるDPについて貰うDP、配るDPを説明しているので、是非参考にしてください。
貰うDPと配るDPの解き方の例(Python)
Pythonのコードだけですみませんが、解法の例を以下に置きます。
もちろん例であって、全く同じように解かないといけないというわけではないです。
Pythonによる解き方の例(折り畳みコード)
H, W = map(int, input().split())
Field = [list(map(int, input().split())) for _ in range(H)]
# 解き方の例1(貰うDP)
# 現在のタイルを正方形の右下端とする最大面積の1辺の長さを求める貰うDP
# -1は未確定状態とする
get_dp = [[-1]*W for _ in range(H)]
for h in range(H):
for w in range(W):
if Field[h][w] == 0:
# 左、上、左上の3方向のいずれか1方向からでも貰うことがない端側の綺麗なマスの面積は1とする
if h == 0 or w == 0:
get_dp[h][w] = 1
else:
# 貰う処理、貰う3箇所は値が確定している
get_dp[h][w] = min(get_dp[h-1][w], get_dp[h][w-1], get_dp[h-1][w-1])+1
else:
# 汚ければ面積は0
get_dp[h][w] = 0
get_ans = 0
# 最大の値を確認する
for gd in get_dp:
get_ans = max(max(gd)**2, get_ans)
# 解き方の例2(配るDP)
# 現在のタイルを正方形の右下端とする最大面積の1辺の長さを求める配るDP
# infは未確定状態とする
inf = 999999
deliver_dp = [[inf]*W for _ in range(H)]
for h in range(H):
for w in range(W):
if Field[h][w] == 0:
# 左、上、左上の3方向のいずれか1方向からでも配られることがない端側の綺麗なマスの面積は1とする
if h == 0 or w == 0:
deliver_dp[h][w] = 1
else:
# 汚ければ面積は0
deliver_dp[h][w] = 0
# この段階で、deliver_dp[h][w]の値が確定
# 配る処理、そのタイルの値から配る側のタイル側に向け、あり得る最大値を更新していく
if h < H-1:
deliver_dp[h+1][w] = min(deliver_dp[h+1][w], deliver_dp[h][w]+1)
if w < W-1:
deliver_dp[h][w+1] = min(deliver_dp[h][w+1], deliver_dp[h][w]+1)
if h < H-1 and w < W-1:
deliver_dp[h+1][w+1] = min(deliver_dp[h+1][w+1], deliver_dp[h][w]+1)
deliver_ans = 0
# 最大の値を確認する
for dd in deliver_dp:
deliver_ans = max(max(dd)**2, deliver_ans)
# 貰うDPも配るDPも等しい結果となる
print(get_ans, deliver_ans)
問い:貰うDPと配るDPに有利不利はなく同じと思ってよいのか
一般的な結論としては、同じと思ってよくて、問題によって解きやすいと感じる方を選べばよいとなります。
例えばナップサックDPや桁DPと呼ばれるものは、配るDPで解かれている場合が多い気がします。
ただし、C++やRustに比べて処理速度が遅くTLE (実行時間超過)しがちなPythonを使用する場合について、最小値や最大値を求めていくDPでは、貰うDPを使用する方が少なからずよいのではという考えにたどり着きました。
貰うDPでは、貰う側の情報の結果を計算した上で配列に1度代入するだけでよいですが、配るDPでは、配列にある配り先へ更新の都度代入を行います。
つまり、配るDPは配列に対する代入回数が増える傾向にあります。
Pythonは代入処理や巨大な配列や2次元配列へのアクセスは速度が遅く、TLE しがちです。
実は上記問題について、貰うDPの提出ではAC (正解)となりましたが、配るDPの提出ではTLEしてしまったのです。
とは言え、年単位で競技プログラミングに参加していますが今回記事を書く上で初めて気付いたことなので、ほとんど役に立たない知識になると思われます。
まとめとしてこの記事からなんとなーくでいいので理解が増えたら嬉しかったこと
- 正方形をどれだけ大きくできるかは1つ上、1つ左、1つ左上のマスの同じ情報から高速に求めることができる
- DPとは値が確定している結果を再利用して処理を高速化させるアルゴリズムのこと
- 合算する以外のDPも存在する
- 1次元DPも2次元DPも解き方の発想は同じ
- 貰うDPも配るDPも最終的な結果が等しく求められるので、問題に合わせて好きな方を使えばよい
逆にやめておいた方がよいこと
- ビジュアライザからhtmlとかcssとかjavascriptを理解しようとすること
(正直フロントエンドはほぼ独学で一般的に正しく書けてるか怪しいですし、ソース見るのもやめてくれると嬉しいです…重い処理に対してWebAssembly使おうと考えていたものの、環境構築に躓いてる間に雑に作り上げてしまい…) - ビジュアライザのバグを探そうとすること
- 「これマスにマウスを乗せると点滅するんだ。でも、ステップ中にマウス動かすとなんか変な点滅の仕方するな。どんなコードだろ。え、もしかしてステップ変わる際に表全部書き換えてるの? それでマウスオーバーしてるマスの色は変えたいけどステップの切り替わりの瞬間にちらつくから、それを隠すように点滅させるようにしたんだ。よく考えたね。なんて言うとでも思ったか。万死に値する」と書き込むこと
補足
今回の内容で最大正方形の求め方は理解できるかなと思います。
では、最大長方形を求める方法はどうなるでしょうか。気になりますよね。
これも動的計画法などを使用して $O(HW)$ で解くことができますが、難易度はグンと上がります。
実は元々想定していたビジュアライズは最大長方形を求めるものでした。
しかし、どうも上手く表現できる気がしなかったため諦めて今回のページを作成したという経緯があります。
最大長方形の求め方が気になった方は是非調べてみたください! また、よければビジュアライズに挑戦してみてください!
ちなみに、この記事を開いた方で競技プログラミングやAtCoderが気になるなーという方がいましたら、是非以下の記事を読んでみてください。
毎年春は新規の参加者が増える傾向にあるので、今がはじめ時ですよ!