車輪移動ロボットでデジタルツイン

はじめに

子どものプログラミング教材として、MicrobitやArduinoを搭載した、車輪移動ロボット（対向2輪型）が発売されています。
（例えば、360度サーボモータを使ったサーボカーキット Microbitで360度サーボモータを動かす)
ロボットにいろいろな動き、無線で操作、センサーをつけて自律的に操作すようなサンプルプログラムが教材として提供されています。
もう一歩踏み込んで、この動きをあらかじめシミュレーションする、実際に動かしたデータから軌跡を再現するといった、データを使った、サイバー空間（デジタル空間）とフィジカル空間（実空間）を結ぶ（デジタルツイン）ものがあれば面白いと思いました。そこで、移動ロボットのモーターON/OFFの情報から軌跡を再現するシミレーションを作ってみました。なお、モーター（またはサーボモーター）のON/OFF情報の取り出しは、今後の課題で、今回はその部分は含めていません。

車輪移動ロボット

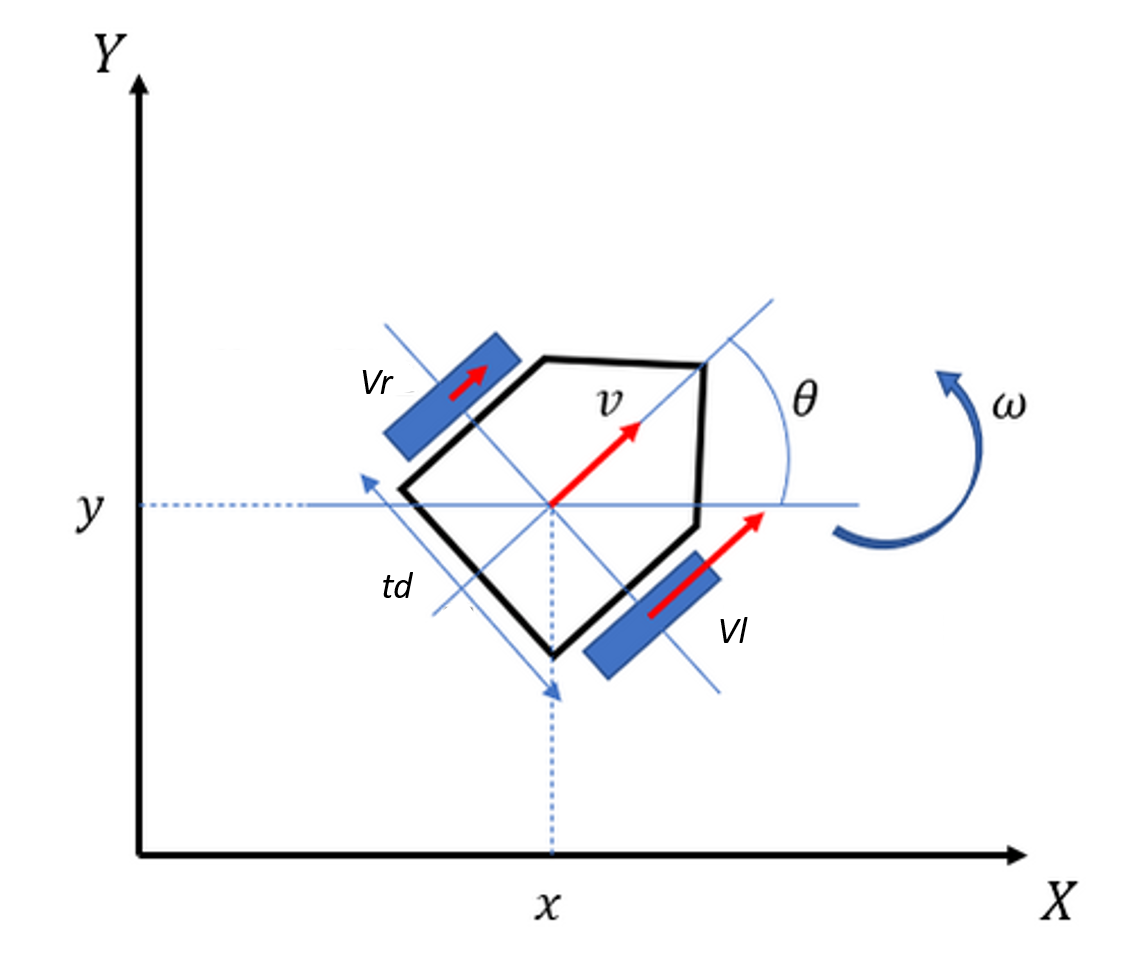
車輪移動ロボットについては、下記のサイトが参考になりますが、入力は左右の車輪の速度で、設定する値として車輪間の長さがあります。
式は、以下の様になります。

v: velocity \\

    \omega: angular \ velocity \\

     x, y: position\\
     \theta: directon　\ angle\\
     t_d: tread

v _k = (v_r +v_l)/2 \\
\omega _k = (v_r +v_l)/t_d \\

x_{k+1} = x_k + \cos \theta _k\cdot\Delta K v_k \\
y_{k+1} = y_k + \sin \theta _k\cdot\Delta K v_k \\
\theta _{k+1} = \theta _k + \Delta K \omega _k \\

図：車輪移動ロボットの座標とパラメータ（参考にした記事の図を一部変更）

参考　車輪移動ロボット原理
移動するメカ・ロボットと 制御の基礎 - 東北学院大学情報処理 ...
車輪ロボット（対向2輪型）の運動を計算してみよう

Pythonによるシミレーション

参考にしたコード
Two wheel motion model sample

今回のシミレーションでは、左右の両輪の速度は一定としてON/OFFのみの情報としています。

移動	右車輪	左車輪
直線	前ON	前ON
後進	後ON	後ON
右折	OFF	前ON
左折	前ON	OFF
その場回転	前ON（後ON）	後ON（前ON）

プログラム環境

Win 10 Pro 64bit
Anaconda
python 3.7

プログラムコード

"""
対向2輪型ロボット
軌跡シミュレーション

入力パラメータ
2つの車輪の間の長さ：tread [m]
車輪の速度　右、左：vr, vl [m/s]

出力
車重心位置の速度：ver
旋回角速度：omega [rad/s]

最終出力
方位角：thetat
x,y座標: xt ,yt


参考にしたコード
Two wheel motion model sample
https://www.eureka-moments-blog.com/entry/2020/04/05/180844#%E5%AF%BE%E5%90%912%E8%BC%AA%E5%9E%8B%E3%83%AD%E3%83%9C%E3%83%83%E3%83%88
変更点：
行列形式を普通の式に展開
車輪の角速度から車輪の速度に変更
シミレーション入力を変更

アニメーション
Pythonでグラフ（Matplotlib）のアニメーションを作る（ArtistAnimation編）
https://water2litter.net/rum/post/python_matplotlib_animation_ArtistAnimation/

[Pythonによる科学・技術計算] 放物運動のアニメーションを軌跡(locus)付きで描画, matplotlib
https://qiita.com/sci_Haru/items/278b6a50c4e9f4c07dcf

"""

import numpy as np
from math import cos, sin, pi
import math
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation

def twe_wheel_fuc(v, state, delta, factor=1, td=2):
    """
    Equation of state
    Args:
        v (tuple or list): velocity of each wheel unit m/s,(right velocity,left velocity)
        state (list):　state [x, y, thita] , x, y 
        delta (float): update time unit s
        factor (float):velocity factor Defaults to 1
        td (float): tread length between wheel unit m Defaults to 2.

    Returns:
        [list]: next state
    """
    # vr: right wheel velocity, vl:left wheel velocity
    # vel: Center of gravity velocity
    # omega: Rotation angular velocity
    vr = v[0]*factor
    vl = v[1]*factor
    vel = (vr + vl)/2
    omega = (vr - vl)/(td)
    # state[2]: theta
    x_ = vel*delta*cos(state[2]+omega*delta/2)
    y_ = vel*delta*sin(state[2]+omega*delta/2)
    # x_ = vel*delta*cos(state[2])
    # y_ = vel*delta*sin(state[2])
    xt = state[0] + x_
    yt = state[1] + y_
    thetat = state[2]+omega*delta
    update_state = [xt, yt, thetat]
    return update_state


def simulation_twewheel(data,ini_state=[0,0,0],factor=1,td=6.36):
    """
    data: list On/OFF data

    """
    # simulation
    #アニメーショングラフ描画のため
    fig = plt.figure()
    ims = [] 
    #計算データ（座標）の格納
    st_x = []
    st_y = []
    st_theta = []
    st_vec = ini_state

    for i in data:   
        st_vec = twe_wheel_fuc(i, st_vec, delta=1,factor=factor,td=td)
        xt, yt, thetat = st_vec
        print("State:",st_vec)
        print("Direction angle: ",math.degrees(thetat))
        st_x.append(xt)
        st_y.append(yt)
        st_theta.append(thetat)

        #Plotのための設定
        plt.grid(True)
        plt.axis("equal")
        plt.xlabel("X")
        plt.ylabel("Y")

        #　時刻tにおける位置だけならば
        # im=plt.plot(xt,yt,'o', color='red',markersize=10, linewidth = 2)

        # 時刻tにおける位置と，時刻tに至るまでの軌跡の二つの絵を作成
        plt.annotate('', xy=(xt+cos(thetat),yt+sin(thetat)), xytext=(xt,yt),
                    arrowprops=dict(shrink=0, width=1, headwidth=2, 
                    headlength=10, connectionstyle='arc3',
                    facecolor='blue', edgecolor='blue'))
        im=plt.plot(xt,yt,'o',st_x,st_y, '--', color='red',markersize=10, linewidth = 2)

        ims.append(im)

    # アニメーション作成
    anim = ArtistAnimation(fig, ims, interval=100, blit=True,repeat=False) 
    plt.show()
    # plt.pause(10)

if __name__ == '__main__':
    # 1秒ごとのvelocityデータ
    #スイッチON/OFFとして速度は一定とする。正回転：1、逆回転：-1、停止：0
    #(1,1)：前進、（0,1)：右回り、（1,0)：左回り、(-1,1) or (1,-1)：その場回転
    input_lists =[(1,1),(1,1),(1,1),(1,1),(1,1),(1,1),
                  (0,1),(0,1),(0,1),(0,1),(0,1),(0,1),
                  (1,1),(1,1),(1,1),(1,1),(1,1),(1,1),
                  (1,0),(1,0),(1,0),(1,0),(1,0),(1,0),
                  (1,1),(1,1),(1,1),(1,1),(1,1),(1,1),
                  (1,-1),(1,-1),(1,1),(1,1),
                  (1,-1),(1,-1),(1,1),(1,1),
                  (1,0),(1,0),(1,0),(0,1),(0,1),(0,1),
                  (1,0),(1,0),(1,0),(0,1),(0,1),(0,1),
                  (1,1),(1,1),]

    input_lists2 =[(1,1),(1,1),(1,1),(1,1),(1,1),(1,1),]

    simulation_twewheel(data=input_lists,ini_state=[0,0,0],factor=1,td=6.36)

プログラムコードについて、Kiotoさんからアドバイスを頂きました。感謝いたします。

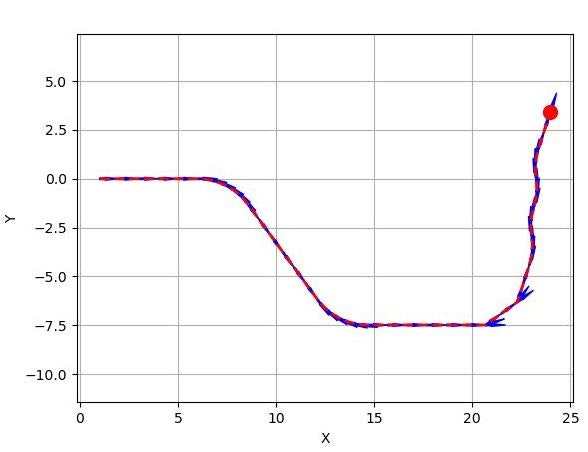
結果

input_list1をデータとして読み込ませたときの結果

まとめ

デジタルツイン（サイバー空間とフィジカル空間）では、データを介してつなげることができます。フィジカル空間からデータが、サイバー空間ではデータによるシミュレーションまたは、シミュレーションによるデータがその橋渡しとなります。プログラミング教育からデータ活用教育まで広がっていけばと思っています。