はじめに
この記事では高速かつ高性能な単語分散表現Gloveについて記述しています。自然言語処理に馴染みのない方もために一応、ざっくりとした順を追って説明します。
自然言語をコンピューターで扱う場合
言語情報をコンピューターで扱うときにOne Hotと呼ばれる表現が良く使われます。
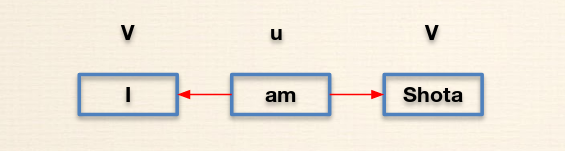
例えば'I am Shota'という文章があれば辞書を用意しておき、辞書に観測された部分は1をつけてそうでない部分は0にするような表現になります。
当然、辞書にない単語は扱えないのでShotaは何もカウントされません。
一般的にこのような場合は<UNK>と呼ばれるUnkown Wordの略で補います。
上記の手法ですと下記のデメリットがあります。
- メモリ空間を辞書のサイズ分取る
- 辞書にない単語を扱えない
- ’は’、’と’などの助詞と固有名詞を同等に扱う
- 計算コストが高い
シンプルな手法ですが上記の問題があります。
次元圧縮方法
そのために次元を減らす手法としてWord2Vecや単語の共起行列の次元を減らすSVDなどの手法が使用されています。
- Word2Vecについて
先ほどの例を用いると下記のように辞書のサイズ分のベクトルを用意せずに次元圧縮してかつ意味のある表現にできます。
- 単語の共起行列の次元を減らすSVDについて
下記のような単語の共起行列を用意して、その次元を減らすための手法としてSVDを用います。
Natural Language Processing with Deep Learning 15ページ参照
Word2Vec、SVDによる次元圧縮の利点と欠点
Word2Vec
- 利点:文章の意味や構文情報を上手く捉えることができる
- 欠点:Windowを使用するため文章全体のトピックは考慮できない
SVD
- 利点:文章全体の情報を使用するため文章全体のトピックを考慮できる
- 欠点:大きなコーパスに適用する場合、計算時間に問題がある
Glove
上記の良い所取りをしたのがGloveです。
Gloveの利点
- 学習が速い
- 精度が高い
- 小さいコーパスでも動作可能
小さいコーパスや学習が速い理由は共起行列を学習に加えているため良い初期値が得られるからだと思われます。
Word2Vecとの違いはこの部分にあります。
ここでどのように共起行列を導入しているか最適化関数を見てみます。
J(\theta) = \frac{1}{2}\sum^{W}_{i,j=1}f(P_{ij})(u^{T}_{i}v_j - \log{P_(ij)})^2
まず共起行列を表しているのがP_ijになります。
P_ijの行列に対してf(P_ij)は共起行列の重みになります。これは頻度の高い助詞などを不当に高く与えないように単語の頻度が一定以上の場合は小さくするような処理をしている重み行列になります。
pythonで共起の重み行列を計算すると下記のようになります。
(w_i, w_j)が共起の単語を表し、一定以上の頻度、今回は100以上の場合は固定値に集約しています。
try:
x_ij = X_ik[(w_i, w_j)]
except:
x_ij = 1
x_max = 100
alpha = 0.75
if x_ij < x_max:
result = (x_ij / x_max) ** alpha
else:
result = 1
return result
uは元となる単語でvはターゲットとなる単語です。Skipグラムなどの手法だと文章にある単語から周りの単語を予測するような形になります。
下記のような形です。
実装について
ここからは実際のコードを見て処理を追っていきます。
データ準備
前処理の部分です。
日本語のファイルを読み込む想定なので下記のようにエンコードをしています。
def read_file(file_name: str):
with codecs.open(file_name, 'r', encoding='utf-8', errors='ignore') as f:
read_data = f.read().split('\n')
read_data = list(map(methodcaller("split", " "), read_data))
return read_data
読み込んだ結果は各単語を要素としてもつリストをまとめてもつリストになります。
[['"', 'I', 'thought', 'so', '.'], ['All', 'right', ';', 'take', 'a', 'seat', '.'], ['Supper', '?--', 'you', 'want', 'supper', '?'], ['Supper', "'", 'll', 'be', 'ready', 'directly', '."']]
コンピューター上ではインデックスで扱った方が扱いやすいのでその形に変換する辞書が必要なので読み込んだデータは下記のような形式に直します。
- 単語とインデックスの表現
{'': 0, '</s>': 1, '、': 2, '。': 3, 'が': 4}
インデックスでは人には分からないので逆の変換とかけられるようにインデックスと単語の表現も用意します。
- インデックスと単語の表現
{0: '', 1: '</s>', 2: '、', 3: '。', 4: 'が'}
下記が実装になります。辞書の順を一定にしてテストしやすいようにソートしています。
def __make_word2index(self, vocab: list=[]):
word2index = {}
for vo in vocab:
if vo not in word2index.keys():
word2index[vo] = len(word2index)
index2word = {v: k for k, v in word2index.items()}
word2index = dict(collections.OrderedDict(sorted(word2index.items(),
key=lambda t: t[1])))
index2word = dict(collections.OrderedDict(sorted(index2word.items(),
key=lambda t: t[0])))
return word2index, index2word
Word2Vecと同様にwindow幅ごとに処理を行うためwindowを用意するのが下記の処理になります。
def __make_window_data(self, window_size: int=5,
corpus: list=[]):
windows = flatten([list(nltk.ngrams(['<DUMMY>'] * window_size + c +
['<DUMMY>'] * window_size,
window_size*2+1)) for c in corpus])
window_data = []
for window in windows:
for i in range(window_size*2 + 1):
if i == window_size or window[i] == '<DUMMY>':
continue
window_data.append((window[window_size], window[i]))
return window_dat
共起行列の重みを作成する部分が下記になります。
combinations_with_replacementで重複した組み合わせを取得できます。
>>> list(itertools.combinations_with_replacement(A, 3))
[('a', 'a', 'a'),
('a', 'a', 'b'),
('a', 'a', 'c'),
('a', 'b', 'b'),
('a', 'b', 'c'),
('a', 'c', 'c'),
('b', 'b', 'b'),
('b', 'b', 'c'),
('b', 'c', 'c'),
('c', 'c', 'c')]
逆方向の共起も必要なのでX_ik[bigram[1], bigram[0]] = co_occer + 1のような処理が入っています。
def __make_co_occurence_matrix(self,
window_data: list=[],
vocab: list=[]):
X_ik_window_5 = Counter(window_data)
X_ik = {}
weightinhg_dict = {}
for bigram in combinations_with_replacement(vocab, 2):
if bigram in X_ik_window_5.keys():
co_occer = X_ik_window_5[bigram]
X_ik[bigram] = co_occer + 1
X_ik[bigram[1], bigram[0]] = co_occer + 1
else:
pass
weightinhg_dict[bigram] = self.__weighting(X_ik=X_ik,
w_i=bigram[0],
w_j=bigram[1])
weightinhg_dict[bigram[1], bigram[0]] = \
self.__weighting(X_ik=X_ik, w_i=bigram[1], w_j=bigram[0])
weightinhg_dict = dict(collections.OrderedDict(
sorted(weightinhg_dict.items(), key=lambda t: t[1])))
return X_ik, weightinhg_dict
モデル
下記がGloveのモデルのforwardの順伝搬処理です。
- 先ほどの最適化式の
uを中心となる単語、vを予測したい単語とおいて重みとバイアスを計算しています。 - 計算した中心単語と予測単語の重みの行列式を計算
- 最後の部分で最適化式を実現しています。
def forward(self, center_words, target_words, coocs, weights):
center_embeds = self.embedding_v(center_words)
target_embeds = self.embedding_u(target_words)
# Reference(squeeze)
# http://pytorch.org/docs/master/torch.html#torch.squeeze
center_bias = self.v_bias(center_words).squeeze(1)
target_bias = self.u_bias(target_words).squeeze(1)
inner_product = target_embeds.bmm(center_embeds.transpose(1, 2)).squeeze(2) # noqa
loss = weights * torch.pow(inner_product + center_bias + target_bias - coocs, 2) # noqa
return torch.sum(loss)
学習
先ほど用意したデータを取得して学習を行います。
torch.catの処理ですが下記のようにデータを演算しやすい形に変更する処理になります。
x
-0.9697 0.1701 -0.5611
0.0019 -0.1810 0.1066
[torch.FloatTensor of size 2x3]
torch.cat(x)
-0.9697
0.1701
-0.5611
0.0019
-0.1810
0.1066
[torch.FloatTensor of size 6]
データを演算しやすい形に変更し、勾配を0で初期化しロスを計算し誤差逆伝搬処理の後に最適化処理を行います。
for epoch in range(self.epoch):
for i, batch in enumerate(get_batch(batch_size=self.batch_size,
train_data=train_data)):
inputs, targets, coocs, weights = zip(*batch)
inputs = torch.cat(inputs)
targets = torch.cat(targets)
coocs = torch.cat(coocs)
weights = torch.cat(weights)
self.model.zero_grad()
loss = self.model(inputs, targets, coocs, weights)
loss.backward()
self.optimizer.step()
losses.append(loss.data.tolist()[0])
結果
Twitterのデータ428文で4170単語で実験しました。
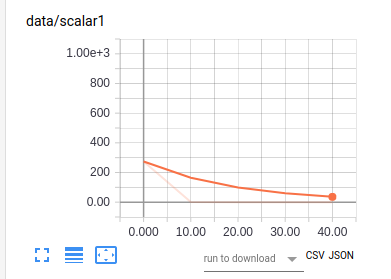
Tensorboardで結果を出力しました。
ロスを見る限り学習は動作しているようです。
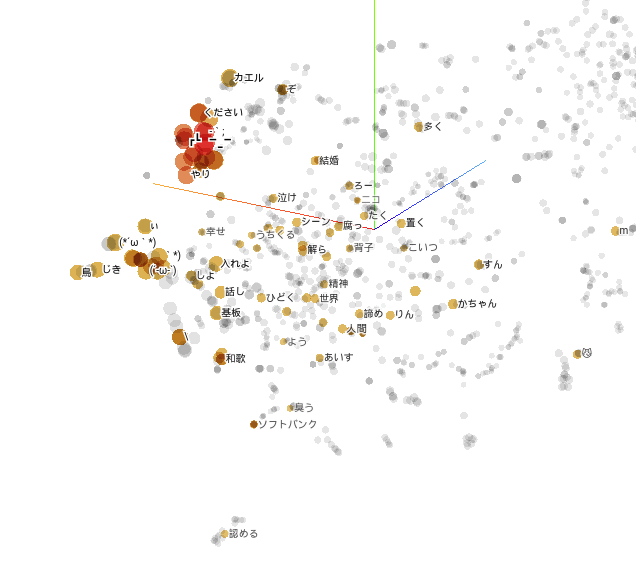
では肝心の分散空間はどうでしょうかよく分からない結果でしたwww
顔文字は近くになっているので良いのかな????
コード
コードはテストなど直す部分が必要ですが公開はしています。後ほど修正します。
最後に
時間があってもっと深く知りたい方は下記を見ることをお薦めします!!!
Lecture 3 | GloVe: Global Vectors for Word Representation
参考