こんにちは、事業会社で働いているデータサイエンティストです。
皆さん、せっかく良いベイズ統計・ベイズ機械学習モデルを作ったのに、「うまくデプロイできない…」という状況に直面したことはありませんか?
本記事では、ベイズモデルの本質を押さえたシンプルなトイモデルを用いて、ベイズ統計モデルをどのようにシステム全体の設計に組み込むべきか、そして、おそらくベイズ統計に馴染みのない、あるいは慎重な姿勢を持つエンジニアチームとどう連携すればよいのかについて、ビジネスの現場でベイズモデルを扱ってきた私なりの考えを共有します。
本記事では主に Stan を扱いますが、ここで紹介する考え方はすべての確率的プログラミング言語に共通します。したがって、NumPyro や PyMC のユーザーの方にも、きっと参考になるはずです。
かなり長い内容になりますので、まずはこの記事で最も伝えたい結論からお話ししましょう:
- 係数表(パラメータ表)と計算方法の仕様を共有して、実装はエンジニアに任せよう
- 確率的プログラミングをそのままプロダクションに載せるのは、全力で避けよう
- エンジニアと初めてモデルのデプロイについて話すときは、数学の話はなるべく隠そう
では、まずはトイモデルから入りましょう!
ベイズモデルの説明
真のデータ生成過程
データは、次のように生まれたとします:
$$
\epsilon_{i} \sim Normal(0, 1)
$$
$$
y_{i} = \beta_{pref_{pref_{i}}} + price_{i} \cdot \beta_{price} + sin(t_{i}) + t_{i} + \epsilon
$$
要するに、$y_{i}$(ここでは購買数とします)は、都道府県効果($\beta_{pref}$)、価格効果($\beta_{price}$)、そして時間効果($sin(t_{i}) + t_{i}$)の3つで構成されているということです。ここで、都道府県は ABC の3つがあるとしましょう。
正解となる係数の値は以下のとおりです:
| 係数 | 値 |
|---|---|
| $\beta_{pref_{A}}$ | 0.5 |
| $\beta_{pref_{B}}$ | 1.2 |
| $\beta_{pref_{C}}$ | -0.5 |
| $\beta_{price}$ | -0.8 |
では、早速シミュレーションで学習データと検証データを作りましょう:
set.seed(12345)
df <- 50000 |>
rnorm() |>
tibble::tibble(
e = _
) |>
dplyr::mutate(
pref = sample(c("A", "B", "C"), dplyr::n(), replace = TRUE, prob = c(0.3, 0.1, 0.6)),
price = rnorm(dplyr::n()),
t = sample(1:50, dplyr::n(), replace = TRUE),
pref_effect = dplyr::case_when(
pref == "A" ~ 0.5,
pref == "B" ~ 1.2,
TRUE ~ -0.5
),
y = pref_effect - 0.8 * price + sin(t) + t + e
)
df_test <- 1000 |>
rnorm() |>
tibble::tibble(
e = _
) |>
dplyr::mutate(
pref = sample(c("A", "B", "C"), dplyr::n(), replace = TRUE, prob = c(0.3, 0.1, 0.6)),
price = rnorm(dplyr::n()),
t = sample(1:50, dplyr::n(), replace = TRUE),
pref_effect = dplyr::case_when(
pref == "A" ~ 0.5,
pref == "B" ~ 1.2,
TRUE ~ -0.5
),
y = pref_effect - 0.8 * price + sin(t) + t + e
)
推定されるベイズ統計モデル
さて、今回はシミュレーションで生成されたデータを使っているため、私たちはデータ生成過程の「正解」を知っています。
しかし、実際のデータ分析では、特に時間の効果が $sin(t) + t$ のように複雑な形になる場合、事前にその形を正確に把握するのは困難です。そのため、柔軟なモデルを使って、自動的かつデータドリブンに近似させる必要があります:
$$
f(t) \approx sin(t) + t
$$
本記事では、私がこの前考案したアテンション機構モデルで、$f(t)$ を推定します:
ほぼ上の記事の再掲になりますが、全体の構造から説明すると、こうなります:
$$
f(t) = softmax(アテンションスコア(t)) '\cdot \beta
$$
ここで、$アテンションスコア$も$\beta$も無限次元のベクトルです。続いて、アテンションスコアの要素$d$の指数変換はこのように計算されます:
$$
exp(アテンションスコア_{d}(t)) = \omega_{d} \cdot \left( \frac{1}{\sqrt{2\pi} \sigma_{d}} \exp\left( -\frac{1}{2} \left( \frac{t - \mu_{d}}{\sigma_{d}} \right)^2 \right) \right)
$$
ここで、$\mu_{d}$は要素$d$が担当する時間の中心、$\sigma_{d}$はその要素が管轄する時間の広がり(分散)を表します。したがって、例えばある時点$t$が要素1の中心$\mu_1$と要素2の中心$\mu_2$の間にあり、$\mu_1$に近い場合、その時点のトレンド成分は$\beta_1$の影響を強く受けつつも、$\beta_2$の影響も少し受け、結果として$\beta_1$と$\beta_2$の加重平均として表現されます。
この構造は、ChatGPTの中核にもなっているアテンション機構(論文リンク)と非常に似ています。具体的には:
- 時点$t$が「クエリ(query)」として機能し、
- 各要素$d$の中心$\mu_{d}$と範囲$\sigma_{d}$が「キー(key)」として、
- トレンドパラメータ$\beta_{d}$が「バリュー(value)」として振る舞います。
そして、
$$
アテンションスコア_d(t) \quad \leftrightarrow \quad \text{クエリとキーの類似度スコア}
$$
に相当し、
$$
softmax(\text{アテンションスコア}(t))
$$
で各要素の重要度(注意重み)を計算し、これを値($\beta$)の重みとして加重平均することで、最終的なトレンド$f(t)$を得ています。
このように、トレンド成分は時間ごとに異なるトレンド「プロトタイプ」へ注意を向け、重み付きの平均を取ることで柔軟に変化を表現しています。
ここではさらに、要素の数を研究者の恣意的な意思決定ではなく、データドリブンな形で判断するため、$\omega_{d}$がすぐゼロに収束するよう、棒折り過程で構築します。
具体的には、要素の重要度を決定するためのハイパーパラメータ $\gamma$ を、以下のようにガンマ分布からサンプリングします:
$$
\gamma \sim Gamma(1, 1)
$$
続いて、棒折り過程に基づき、各要素 $d$ に対応する重み $\omega_d$ を構築します:
$$
\delta_d \sim Beta(1, \gamma)
$$
$$
\omega_d = \delta_d \prod\limits_{l=1}^{d - 1} (1 - \delta_l)
$$
この処理は $d = 1$ から $d = \infty$ まで理論的に繰り返されます。ただ、$\omega_{d}$がすぐゼロに収束するため、実際は有限個の要素しか利用されません。
よって、$y_{i}$ を下記の式で推定します:
$$
y_{i} = \beta_{pref_{pref_{i}}} + price_{i} \cdot \beta_{price} + f(t_{i}) + \epsilon
$$
パラメータの事前分布は下記のStanコードをご参照ください:
functions {
vector stick_breaking(vector breaks){
int length = size(breaks) + 1;
vector[length] result;
result[1] = breaks[1];
real summed = result[1];
for (d in 2:(length - 1)) {
result[d] = (1 - summed) * breaks[d];
summed += result[d];
}
result[length] = 1 - summed;
return result;
}
}
data {
int pref_type;
int time_type;
int approx_type;
array[time_type] real time_seq;
int N;
array[N] int pref;
vector[N] price;
array[N] int time;
array[N] real y;
int val_N;
array[val_N] int val_pref;
vector[val_N] val_price;
array[val_N] int val_time;
}
parameters {
real<lower=0> rho_global;
vector<lower=0>[pref_type] rho_pref;
real<lower=0> rho_price;
vector<lower=0>[approx_type] rho_trend_beta;
real intercept;
vector[pref_type] beta_pref_unnormalized;
real beta_price;
real<lower=0> trend_alpha;
vector<lower=0, upper=1>[approx_type - 1] trend_breaks;
vector[approx_type] trend_midpoint;
vector<lower=0>[approx_type] trend_spread;
vector[approx_type] trend_beta;
real<lower=0> sigma;
}
transformed parameters {
vector[pref_type] beta_pref;
simplex[approx_type] trend_dimension;
vector[time_type] f_trend;
beta_pref = beta_pref_unnormalized - mean(beta_pref_unnormalized);
trend_dimension = stick_breaking(trend_breaks);
for (i in 1:time_type){
vector[approx_type] case_when;
for (j in 1:approx_type){
case_when[j] = log(trend_dimension[j]) + normal_lpdf(time_seq[i] | trend_midpoint[j], trend_spread[j]);
}
f_trend[i] = softmax(case_when) '* trend_beta;
}
}
model {
rho_global ~ cauchy(0, 1);
rho_pref ~ cauchy(0, 1);
rho_price ~ cauchy(0, 1);
rho_trend_beta ~ cauchy(0, 1);
beta_pref ~ normal(0, (rho_global * rho_pref)^2);
beta_price ~ normal(0, (rho_global * rho_price)^2);
trend_alpha ~ gamma(1, 1);
trend_breaks ~ beta(1, trend_alpha);
trend_midpoint ~ normal(0, 10);
trend_spread ~ inv_gamma(5, 5);
trend_beta ~ normal(0, (rho_global * rho_trend_beta)^2);
sigma ~ inv_gamma(5, 5);
y ~ normal(beta_pref[pref] + beta_price * price + f_trend[time], sigma ^ 2);
}
generated quantities {
array[val_N] real predict;
predict = normal_rng(beta_pref[val_pref] + beta_price * val_price + f_trend[val_time], sigma ^ 2);
}
モデル推定
ここではまず、都道府県マスターを作って、学習データと検証データに都道府県の ID を付与します:
pref_master <- df |>
dplyr::select(pref) |>
dplyr::distinct() |>
dplyr::arrange(pref) |>
dplyr::mutate(
pref_id = dplyr::row_number()
)
df_with_id <- df |>
dplyr::left_join(pref_master, by = "pref")
df_test_with_id <- df_test |>
dplyr::left_join(pref_master, by = "pref")
次に、モデルのコンパイル:
m_init <- cmdstanr::cmdstan_model("model.stan")
とモデル推定を実施します:
> m_estimate <- m_init$variational(
seed = 12345,
data = list(
pref_type = nrow(pref_master),
time_type = max(df_with_id$t),
approx_type = 20,
time_seq = (1:max(df_with_id$t) - mean(1:max(df_with_id$t)))/(sd(1:max(df_with_id$t))),
N = nrow(df_with_id),
pref = df_with_id$pref_id,
price = df_with_id$price,
time = df_with_id$t,
y = df_with_id$y,
val_N = nrow(df_test_with_id),
val_pref = df_test_with_id$pref_id,
val_price = df_test_with_id$price,
val_time = df_test_with_id$t
)
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.002282 seconds
1000 transitions using 10 leapfrog steps per transition would take 22.82 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -2628533.227 1.000 1.000
200 -361777.514 3.633 6.266
300 -235235.730 2.601 1.000
400 -207823.484 1.984 1.000
500 -226339.801 1.603 0.538
600 -404770.250 1.410 0.538
700 -170676.575 1.404 0.538
800 -158661.218 1.238 0.538
900 -145116.974 1.111 0.441
1000 -132211.324 1.010 0.441
1100 -119971.488 0.920 0.132 MAY BE DIVERGING... INSPECT ELBO
1200 -110791.200 0.302 0.102
1300 -107077.686 0.251 0.098
1400 -99896.395 0.245 0.093
1500 -102449.167 0.240 0.093
1600 -97315.899 0.201 0.083
1700 -96423.896 0.065 0.076
1800 -97478.815 0.058 0.072
1900 -93110.695 0.053 0.053
2000 -91325.081 0.046 0.047
2100 -91472.812 0.036 0.035
2200 -92243.381 0.028 0.025
2300 -91129.561 0.026 0.020
2400 -92969.193 0.021 0.020
2500 -90169.117 0.021 0.020
2600 -91125.583 0.017 0.012
2700 -89785.174 0.018 0.015
2800 -92476.570 0.019 0.020
2900 -89320.728 0.018 0.020
3000 -89451.403 0.016 0.015
3100 -90997.155 0.018 0.017
3200 -88642.059 0.020 0.020
3300 -90094.796 0.020 0.020
3400 -87979.843 0.021 0.024
3500 -89559.550 0.019 0.018
3600 -87701.485 0.020 0.021
3700 -88245.421 0.019 0.021
3800 -87948.615 0.017 0.018
3900 -88119.832 0.014 0.017
4000 -88514.671 0.014 0.017
4100 -88038.175 0.013 0.016
4200 -88333.778 0.010 0.006 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 8.0 seconds.
変分推論なので、N = 50000 の複雑なモデルでも 8 秒で推定が終わりました。
最後に、結果をデータフレイムに整形します:
m_summary <- m_estimate$summary()
モデル推定結果の確認
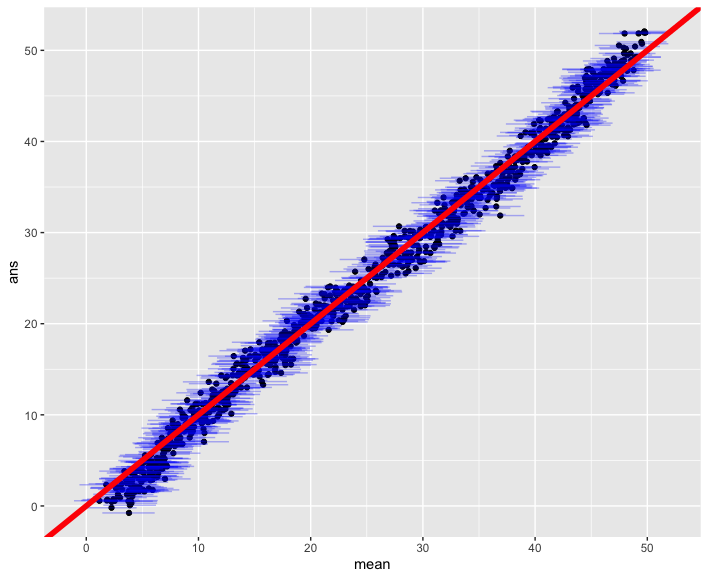
まずは、検証データに対する予測精度を確認してみましょう。横軸は予測結果、縦軸は正解を示しています。青い横の区間は信用区間、赤い線は 45 度線です:
m_summary |>
dplyr::filter(stringr::str_detect(variable, "^predict\\[")) |>
dplyr::bind_cols(
ans = df_test_with_id$y
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = mean, y = ans)) +
ggplot2::geom_errorbarh(ggplot2::aes(xmin = q5, xmax = q95, y = ans), color = ggplot2::alpha("blue", 0.3)) +
ggplot2::geom_abline(slope = 1, intercept = 0, linewidth = 2, color = "red")
ほぼ完璧に 45 度線上にありますので、予測精度はかなり高いです。
次に、値段効果を確認しましょう:
> m_summary |>
dplyr::filter(stringr::str_detect(variable, "^beta_price"))
# A tibble: 1 × 7
variable mean median sd mad q5 q95
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta_price -0.796 -0.796 0.00779 0.00776 -0.809 -0.783
事後分布の平均は正解の -0.8 に近く、かつ瀋陽区間の中にも含まれています。
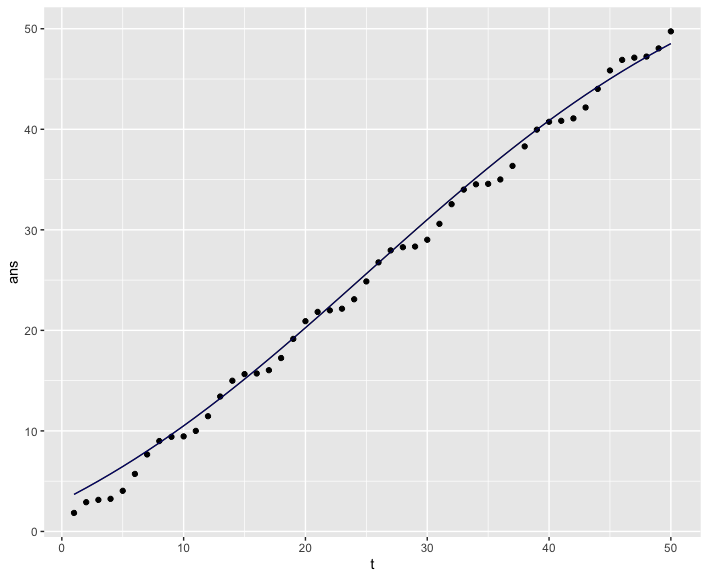
$f(t)$ の推定結果も確認しましょう、点が正解($sin(t) + t$)になります:
m_summary |>
dplyr::filter(stringr::str_detect(variable, "^f_trend\\[")) |>
dplyr::mutate(
t = dplyr::row_number(),
ans = sin(t) + t
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = t, y = ans)) +
ggplot2::geom_line(ggplot2::aes(x = t, y = mean)) +
ggplot2::geom_ribbon(ggplot2::aes(x = t, ymin = q5, ymax = q95), fill = ggplot2::alpha("blue", 0.5))
$sin(t)$ の周期的な変動は捉えられなかったようですが、全体的な上昇傾向は問題なく学習できています。
最後に、都道府県効果を見てみましょう。
beta_pref[1] が A、beta_pref[2] が B、beta_pref[3] が C に対応します。
> m_summary |>
dplyr::filter(stringr::str_detect(variable, "^beta_pref\\["))
# A tibble: 3 × 7
variable mean median sd mad q5 q95
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta_pref[1] 0.0775 0.0766 0.0139 0.0138 0.0552 0.102
2 beta_pref[2] 0.817 0.817 0.0161 0.0166 0.791 0.842
3 beta_pref[3] -0.895 -0.895 0.0117 0.0117 -0.913 -0.875
あれ?ちょっと正解のパラメータと比較する表を作ってみると:
| 係数 | 正解値 | 推定値 | 差 |
|---|---|---|---|
| $\beta_{pref_{A}}$ | 0.5 | 0.0775 | 0.4225 |
| $\beta_{pref_{B}}$ | 1.2 | 0.817 | 0.383 |
| $\beta_{pref_{C}}$ | -0.5 | -0.895 | 0.395 |
まず順序は合っていますが値の差はかなり大きいですね。ただ、差分を計算すると
| 係数の差分 | 正解値 | 推定値 | 差 |
|---|---|---|---|
| $\beta_{pref_{A}} - \beta_{pref_{B}}$ | -0.7 | -0.7395 | 0.0395 |
| $\beta_{pref_{B}} - \beta_{pref_{C}}$ | 1.7 | 1.712 | -0.012 |
| $\beta_{pref_{A}} - \beta_{pref_{C}}$ | 1 | 0.9725 | 0.0275 |
おお!差が小さくなりましたね。そうなんです。このモデルでは都道府県ごとに効果を設定していますが、数学的には都道府県ダミー変数と同様です。共線性の影響により、ダミー変数では都道府県 A の効果という「絶対的な値」を推定するのは難しく、都道府県 A と B の効果差という「相対的な指標」しか推定できないのが一般的です。
なので、差分をうまく推定できた本モデルに特段の問題はありません。
デプロイ方法の説明
ここではまず、モデルから最も距離のある「外側のエンジニア」の心理から説明します。次に、その心理を踏まえて、モデルのデプロイ方法をどう設計し、どのようにエンジニアに伝えるべきかを紹介します。最後に、エンジニアが実装しやすいように、ベイズモデルの設計をどのように工夫すべきかについて述べます。
エンジニアの心理
まずここではっきり言っておきますが、大半のエンジニアは統計学などの数学に詳しくありません。
特に、私のような政治学・経済学出身のデータサイエンティストがジュニアの時期にやりがちなのですが、「工学系出身のエンジニアならベイズ統計と因果推論くらい当然知っているだろう」と勘違いしてしまいます。ですが実際には、ベイズ統計について全く知らないエンジニアが大半です。
その理由はシンプルで、エンジニアが普段取り組んでいるのは、データ指向アプリケーションの開発、ロードバランシング、サーバーサイドレンダリングなどの技術です。これらと統計学は、そもそも関係がないことがほとんどです。詳細は、昨年(2024年)の Japan R で発表した以下の記事をご覧ください:
エンジニアは統計モデルを理解していないからこそ、ビジネスサイド以上に統計モデルに警戒心を持つ傾向があります。その心理は、次のようなものです:
事前分布?尤度関数?馬蹄分布?MCMC?
この人なに言ってるの?
こんな聞いたこともないものをデプロイして、バグが出たら全部俺が直すってこと!?ふざけんな!
こうした反応の結果、統計モデルを使わずに、ローデータから単純集計して平均値を出せば十分ではないか?といった反論が出てくることもあります。
なぜ、エンジニアはビジネスサイドよりも統計モデルに対して警戒心が強いのか?
ビジネスサイドの場合、モデルの背後にあるプロセスや、使用される学習データの定義、推定結果から得られるインサイト、そしてデプロイによって達成される KPI 改善など、最終成果だけを理解していれば業務が進みます。
一方で、エンジニアはそれを全て自分で管理・実装しなければならないという前提で物事を考えるため、「聞いたこともなく、コードに落とした経験もない専門用語」に強く警戒心を抱くのです。
ここまで読んでくださったエンジニアの中で、
いやいや、私たちエンジニアは全員ベイズ統計くらい知ってるよ!
と感じた方がいたら、そのあなたは非常に珍しい存在です。エンジニアの中でも統計学の知識をしっかり身につけた、尊敬すべき方です。
ただ、現実にはあなたのような方ばかりではなく、ほとんどのエンジニアは統計学を深く理解していません。その前提を忘れたまま「エンジニア全員がベイズ統計を理解している」という期待のもとプロジェクトを進めようとすると、データサイエンティストが直面するのと同じ壁にぶつかることになるでしょう。
ぜひ本記事を通じて、あなたほど統計学を知らないエンジニアとどうコミュニケーションを取るべきかの参考にしていただければ幸いです。
エンジニアが統計学を理解していないという前提で考えると、そもそも統計モデルが何をするものなのかという基本的なイメージさえ持っていないことを想定しておいた方がよいです。
極端な例を出すと、あなたが営業商談先の選定を最適化するモデルを構築したとして、次のような反応が返ってくることもあり得ます:
お!モデルを作ってくれたんですね!
じゃあ、その予測値で商談先を降順で並べる機能を作って欲しいな。
あと、営業さんがそのモデルからウーバーイーツを頼んで、商談後に食事できるようにすると最高だね!
さすがに「ウーバーイーツを頼む」は少し誇張かもしれませんが、「商談先を降順に並べる機能」といった要求は現実にあり得ます。
これは、統計モデルの役割が「受注率を予測すること」だという理解がないためです。その結果、モデルを「バックエンド機能そのもの」と誤認識するリスクが生まれるのです。
さて、エンジニアにモデルを伝えるコツに入る前に、まずエンジニアの心理をまとめてみましょう:
- 統計学モデルを警戒する
- 統計学モデルが何をするのかがわからない
エンジニアの警戒を解消するのはとても簡単です。統計学モデルの実装はものすごくシンプルだと伝えたらいいです。ここでは、説明資料とモデルの渡し方について話します。
エンジニアにモデルを伝えるコツ:説明資料
まず、デプロイ方法を説明する場では、数学や統計の話は一切出さないようにしてください。
あらかじめ強調しておきたいのは、これは「エンジニアは統計や数学を知らなくていい」と言いたいわけではありません。むしろ私の考えはその逆で、統計学を正しく理解できる人が多いほうが、データサイエンティストは働きやすくなりますし、会社の経営判断もより合理的になると考えています。だからこそ、エンジニアの皆さんにもぜひ統計学を学んでほしいと思っています。
ただし、モデルのデプロイ方法を説明する場は、そのための場ではありません。そこでは、あくまで「どうやってモデルを使うか」「どうシステムに組み込むか」を伝えるべきです。モデルのデプロイ自体に、統計の知識は必要ありません。
この場でいきなり数式の話を始めると、多くのエンジニアは驚いてしまいます。だからこそ、「デプロイは実はすごく簡単なんですよ」と丁寧に伝えることが重要です。そして、もしモデルの仕組みにも関心を持ってもらえたなら、そのときは別途ミーティングを設定し、統計的な考え方や背景をきちんと説明しましょう。そのうえで、その人の視点からビジネス的にモデルを吟味・批判していただくのが望ましい姿です。
つまり、「デプロイの場ではデプロイだけ」「モデルをビジネス観点で議論する場ではモデルの話をする」。このように目的に応じて適切なコミュニケーションを行うことが、プロジェクトを円滑に進めるためのコツです。
フレンチシェフが突然麻婆豆腐を出してきたら驚きますよね? たとえ麻婆豆腐が好きでも。それと同じです。適切なタイミングで、適切な情報を、適切な形で共有しましょう。
デプロイの際にエンジニア向けに用意する説明資料には、以下の3点が明確に書かれていれば十分です。
- モデルは何を入力データにするのか?
- モデルはどのような方法(ビジネス現場ではこれを「ロジック」と呼びます)で予測結果を計算するのか?
- その予測結果を計算するために必要な材料(データやパラメータなど)はどこにあるのか?
この3点さえ整理されていれば、実装側がモデルをデプロイするうえで困ることは基本的にありません。
エンジニアにモデルを伝えるコツ:モデルの渡し方
その上で、ではどうモデルを渡すのか?まずジュニアのデータサイエンティストがよく考えるのは、Stan、PyMC、NumpyroをそのままDockerでコンテナ化してエンジニアに渡す方法ではないでしょうか?もちろん、深夜で動くようなバッチ(大量の、所定の、予測可能性の高いデータ処理)であればまあ、許されるかもしれませんが、もしプロダクトとして実装し、大量のユーザーが利用すると、まず残念なことに、事後分布のシミュレーションはおそらく遅過ぎて実用に耐えられません。大量のユーザーが利用するサービスは1秒以下の時間を争っています。こんな状態でMCMCで20秒走らせてレコメンドスコアを都度都度計算したい!と言い出しても、おそらくエンジニアチームのリーダーに難色を示されるだけでしょう。もしくはデプロイ後、サイト全体の速度を落として、ユーザーの離脱を招いて止められるでしょう。
また、そもそもの話なんですが、Stan、PyMC、Numpyroのインストールには巨大なファイル群が必要です。この巨大なファイル群がDockerイメージの肥大化を招き、最終的にはデプロイ時の困難を招いてしまう可能性があります。
なので、本番環境でMCMCを回したり、確率的プログラミング言語を直接動かしたりするのはやめた方がいいです。ではどうすればモデルをデプロイすればいいでしょうか?答えは極めて簡単です。本記事が利用するモデルをもう一度確認してください:
$$
y_{i} = \beta_{pref_{pref_{i}}} + price_{i} \cdot \beta_{price} + f(t_{i}) + \epsilon
$$
ここで、予測値の事後分布の平均を求める場合:
$$
\mathbb{E}(y_{i}) = \beta_{pref_{pref_{i}}} + price_{i} \cdot \beta_{price} + f(t_{i})
$$
係数だけでいけちゃうんです!極端にいうと、$f(t)$ は少し複雑そうですが、一旦時間の要素を無視すれば、係数表と都道府県、価格さえわかれば、エクセルでも予測値を吐き出せるはずです。確率的プログラミング言語のサポートは要りません。
ここで、ベイズ統計モデルのパラメータの種類をエンジニアにわかりやすく説明するための話し方について少し紹介します:
-
マスター照合系パラメータ
都道府県、カテゴリなど、テーブルのキーと突き合わせる形で使うパラメータ。 -
掛け算系パラメータ
価格など、何かの入力変数と掛け算する形で使う係数。 -
特殊計算系パラメータ
その他の計算。
マスター照合系パラメータ
まず、もう一度 $\beta_{pref}$ の推定結果を確認しましょう:
> m_summary |>
dplyr::filter(stringr::str_detect(variable, "^beta_pref\\["))
# A tibble: 3 × 7
variable mean median sd mad q5 q95
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta_pref[1] 0.0775 0.0766 0.0139 0.0138 0.0552 0.102
2 beta_pref[2] 0.817 0.817 0.0161 0.0166 0.791 0.842
3 beta_pref[3] -0.895 -0.895 0.0117 0.0117 -0.913 -0.875
beta_pref[X] の X に当たる数値は、都道府県マスターにおける都道府県ID(pref_id)を表しています。したがって、X を整数として抽出すれば、都道府県マスターと LEFT JOIN を行うことで、都道府県名を付与することが可能です:
> m_summary |>
dplyr::filter(stringr::str_detect(variable, "^beta_pref\\[")) |>
dplyr::mutate(
id = variable |>
purrr::map_int(
\(x){
as.integer(stringr::str_split(x, "\\[|\\]|,")[[1]][2])
}
)
) |>
dplyr::left_join(
pref_master, by = c("id" = "pref_id")
)
# A tibble: 3 × 9
variable mean median sd mad q5 q95 id pref
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <chr>
1 beta_pref[1] 0.0775 0.0766 0.0139 0.0138 0.0552 0.102 1 A
2 beta_pref[2] 0.817 0.817 0.0161 0.0166 0.791 0.842 2 B
3 beta_pref[3] -0.895 -0.895 0.0117 0.0117 -0.913 -0.875 3 C
最終的に、不要な列を除いて整形すると、次のようになります:
> m_summary |>
dplyr::filter(stringr::str_detect(variable, "^beta_pref\\[")) |>
dplyr::mutate(
id = variable |>
purrr::map_int(
\(x){
as.integer(stringr::str_split(x, "\\[|\\]|,")[[1]][2])
}
)
) |>
dplyr::left_join(
pref_master, by = c("id" = "pref_id")
) |>
dplyr::select(pref, mean)
# A tibble: 3 × 2
pref mean
<chr> <dbl>
1 A 0.0775
2 B 0.817
3 C -0.895
この状態になれば、エンジニアの方には次のように伝えることができます:
都道府県はマスター照合系パラメータです。
LEFT JOINによってそのレコードの都道府県に対応する効果(meanカラム)を取得してください。
ここで、「事前分布」「尤度関数」「馬蹄分布」「MCMC」といった、エンジニアにとって未知で警戒心を抱かせるキーワードが、LEFT JOIN という、彼らにとって馴染み深く理解しやすい言葉に置き換わりました。LEFT JOIN はエンジニアにとって「自分の言語」です。これにより、警戒心を下げ、信頼関係を築く第一歩となります。
さて、厳密性を重んじるデータサイエンティストであれば、「パラメータの事後分布に伴う不確実性を捨てるのか?」と疑問を持つかもしれません。それに対する答えは、はい、捨てます。
プロダクト実装にはさまざまな制約が伴い、すべてを統計理論の通りに進めることは現実的ではありません。そのため、不確実性を捨て、パラメータの事後分布の平均を使って予測するのは、ある意味でやむを得ない選択です。
もし、このように現実との折り合いをつける考え方に納得できないのであれば、ビジネスの現場ではなく、アカデミア――それも理論研究の世界に戻る方が、あなたにとって幸せかもしれません。複雑なビジネスの世界で、許される範囲で最大限まで統計学的な正しさを担保するアウトプットを提供するのが、データサイエンティストの仕事ですが、その範囲は決して無限ではありません。柔軟な考え方が大事です。
掛け算系パラメータ
続いて、$\beta_{price}$ ですが、これの実装方法はシンプルで、レコードのpriceカラムを持ってきて掛け算すればいいです。
エンジニアの方には次のように伝えることができます:
価格は掛け算系パラメータパラメータです。そのレコードの価格と係数表の
beta_priceの掛け算の結果を取得してください
特殊計算系パラメータ
最後に、$f(t)$ ですが、改めて計算方法を確認すると
$$
f(t) = softmax(アテンションスコア(t)) '\cdot \beta
$$
$$
exp(アテンションスコア_{d}(t)) = \omega_{d} \cdot \left( \frac{1}{\sqrt{2\pi} \sigma_{d}} \exp\left( -\frac{1}{2} \left( \frac{t - \mu_{d}}{\sigma_{d}} \right)^2 \right) \right)
$$
一見すると複雑で、特殊な計算が必要に思えるかもしれませんが、実はこれはマスター照合系にすぎません。なぜなら、確率的プログラミングによって事前に総当たりで結果をすべて計算しておき、それをテーブルとして保存・参照できるからです。
具体的にいうと:
> m_summary |>
dplyr::filter(stringr::str_detect(variable, "^f_trend\\[")) |>
dplyr::mutate(
t = dplyr::row_number()
) |>
dplyr::select(t, mean)
# A tibble: 50 × 2
t mean
<int> <dbl>
1 1 3.68
2 2 4.34
3 3 5.02
4 4 5.72
5 5 6.46
6 6 7.22
7 7 8.00
8 8 8.81
9 9 9.65
10 10 10.5
# ℹ 40 more rows
# ℹ Use `print(n = ...)` to see more rows
のテーブルを、時間をキーに LEFT JOIN すればいいです。
エンジニアの方には次のように伝えることができます:
時間効果はマスター照合系パラメータです。LEFT JOIN によってそのレコードの時間に対応する効果(mean カラム)を取得してください。
この例からもわかるように、特殊計算系のパラメータは、実務ではほとんど登場しません。統計モデルにおける処理の大部分は、マスター照合系パラメータか、掛け算系パラメータとして表現・説明することが可能です。
もし本当に、どうしても事前に計算できないパラメータがある場合は、その計算手順をしっかりとドキュメント化し、エンジニアと丁寧にコミュニケーションを取ることが重要です。
ベイズモデルの設計の工夫
さて、エンジニア関連の話は終わりました。これからはまたモデルの話に戻ります。では、どのようなモデルが望ましいでしょうか?私の経験からすると、答えは簡単です:
予測値の確率分布の期待値を解析的に計算できる
モデルであれば、大きな問題はないでしょう。
例えば、普段よく登場する正規分布回帰モデル、ポワソン分布回帰モデル、ロジスティック回帰モデルの予測値の期待値を解析的に計算できるのはいうまでもありませんが、ガンマ分布といった指数型分布族も概ね問題ありません。これらの分布の期待値は、たいてい文献やウィキペディアで調べれば見つかります。
一方で、例えば次のようなモデルになると、事情が変わってきます:
$$
\eta_{i} = X_{i}'\beta_{\eta}
$$
$$
\lambda_{i} = z_{i}'\beta_{\lambda}
$$
$$
coin_{i} \sim Bernoulli(\eta_{i})
$$
$$
y_i \sim \mathrm{Poisson}(\lambda_i), \quad \text{if } coin_{i} = 1
$$
$$
y_i = 0, \quad \text{if } coin_{i} = 0
$$
このような複雑なモデル、いわゆるゼロ過剰ポワソン分布の場合、まだ期待値を解析的に計算できるかもしれませんが、これよりさらに複雑な確率分布に従って $y_{i}$ が生成されると仮定すると、解析的に解けない領域に入ってしまいます。そうなると、予測にモンテカルロ積分(シミュレーション)が必要となり、計算に必要な時間が大幅に増えてしまいます。
したがって、目的変数が従う確率分布としては、なるべく正規分布、ポワソン分布、負の二項分布、ロジスティック回帰、probit 回帰などのシンプルなものを選んだ方が望ましいです。
事前分布や階層化に関しては、前述のように、推定されるパラメータがマスター照合系・掛け算系・特殊計算系のいずれかに収まっていれば問題なく、分布の形自体はデプロイの難易度とはあまり関係がありません。
結論
いかがでしたか?
本記事では、事業会社でデータサイエンティストとしてベイズモデルをデプロイする際の実践的なアプローチを共有しました。特に、「確率的プログラミング言語をそのまま本番環境に載せるのは全力で避けるべき」という点は、パフォーマンスと運用負荷の観点から非常に重要です。
ベイズモデルのデプロイを成功させる鍵は、モデルの複雑さをエンジニアにそのまま伝えるのではなく、彼らが理解しやすい「係数表(パラメータ表)」と「計算方法の仕様」という形で提供することにあります。特に、統計学的な専門用語を避け、LEFT JOIN のようなエンジニアにとって馴染み深い言葉に置き換えて説明することで、不要な警戒心を解き、スムーズな連携を促せます。
ベイズモデルの特性上、複雑な計算を伴う可能性のある「特殊計算系パラメータ」についても、あらかじめ予測値を総当たりで計算し、マスター照合テーブルとして提供することで、エンジニアの実装を大幅に簡素化できることを示しました。これにより、プロダクトの高速な動作とデプロイの容易さが両立できます。
また、デプロイに適したベイズモデルの設計としては、予測値の期待値を解析的に計算できるシンプルな確率分布を選ぶことが望ましいと述べました。これにより、本番環境でのモンテカルロ積分(シミュレーション)が不要になり、計算時間を大幅に短縮できます。
データサイエンティストとして、統計学的な厳密性を追求することももちろん大切です。しかし、ビジネスの現場では、使えるモデルをいかに早く、効率的にプロダクトに組み込むかという視点も同様に重要です。このバランスを理解し、エンジニアとの円滑なコミュニケーションを意識することが、ベイズモデルを「絵に描いた餅」で終わらせず、実際にビジネス価値を生み出すための第一歩となるでしょう。
ベイズ統計モデルの可能性を最大限に引き出すために、ぜひ本記事で紹介したアプローチを皆さんの現場で試してみてください。
最後に、私たちと一緒に働きたい方はぜひ下記のリンクもご確認ください: