はじめに
こんにちは、事業会社で働いているデータサイエンティストです。
皆さん、統計学や計量経済学の入門講義で、都道府県名や国名といったカテゴリ変数を線形モデルで扱う際には、あるカテゴリ(「東京」「日本」など)を基準カテゴリとしてモデルから抜かなければならない、と学んだ方が多いと思います。理由は、カテゴリ変数は取り得る値が有限であり(都道府県なら 47 種類)、モデルがその「絶対的な貢献度」を識別できないため、相対的な比較しかできないからです。実際、線形モデルを OLS で推定する際に基準カテゴリを抜かずに推定を行うと、推定がうまくいきません。R 言語では、lm 関数が自動的に基準カテゴリを落として処理してくれます。
一方で、基準カテゴリを抜く以外の方法として、カテゴリごとの係数の総和がゼロになるよう制約を課すやり方もあります(例:47 都道府県の係数の和がゼロ)。実務で膨大なカテゴリ変数(例:顧客分析での顧客固定効果)を扱う場合、この総和ゼロ制約の方が扱いやすく、本記事ではこの方法を具体的に紹介します。
ただし、ベイズモデルや Lasso・Ridge などの正則化付きモデルでは、基準カテゴリを抜かなかったり、係数の総和に制約をかけなくても、推定が破綻せず、予測精度も大きく悪化しないことがあります。では、ベイズや正則化を使うならカテゴリ変数に制約をかけなくて良いのか?
本記事では、こうしたモデルを使う場合でも、カテゴリ変数に適切な制約を課す方が、実務で直面する柔軟な予測タスクによりうまく対応できることを示していきます。
実務で直面する柔軟な予測タスクとは?
私の経験では、ビジネスの現場で予測モデルを構築する際、学習時に利用した特徴量と、実際の推論(本番運用)で利用できる特徴量が異なる状況によく直面します。多くの場合、推論時に使える特徴量は、学習時に使った特徴量の部分集合になってしまいます。
例として、次のモデルを考えてみましょう:
$$
購買金額_{i} = \alpha + \beta_{p} \cdot price_{i} + \beta_{\hat{segment_{i}}} + \epsilon
$$
つまり、ユーザーの購買金額は「商品価格」と「ユーザーセグメント」で決まるとします。ユーザーセグメントは、過去の購買履歴から LLM などの深層学習モデルを使って推定されたものとします:
$$
\hat{segment_{i}} = NeuralNetwork(UserHistory_{i}, \theta)
$$
ここで $\theta$ は深層学習モデルのパラメータとアーキテクチャを表します。過去 3 年分のデータと、深層学習モデルによって付与された $\hat{segment_{i}}$ を用いて、次のようにモデルを推定したとします:
$$
\hat{購買金額_{i}} = \hat{\alpha} + \hat{\beta_{p}} \cdot price_{i} + \hat{\beta_{\hat{segment_{i}}}}
$$
この推定式があれば、商品価格とセグメント情報から購買金額を予測できるはずです。しかし、ビジネスの現場はしばしばそう単純にはいきません 😭
例えば、$NeuralNetwork(UserHistory_{i}, \theta)$ の計算が非常に重く、毎日深夜に一度だけバッチ処理を回して前日分のユーザーセグメントを更新しているような場合を考えましょう。
このとき、
- 過去の購買履歴がある既存ユーザー → $\hat{segment_{i}}$ が取得できる
- 新規ユーザー → 購買履歴がないため $\hat{segment_{i}}$ が不明
という問題が発生します。
では、このモデルは使えないのでしょうか?
あるいは、セグメントのない新規ユーザー専用の別モデルを作らないといけないのでしょうか?
この後のシミュレーションで示すように、答えは次の通りです:
過去 3 年分のデータを用いて、セグメント係数に標準化制約を課した回帰モデルを作り、セグメント情報のないユーザーにはセグメント係数を無視して予測するのが最適です。
このアプローチにより、
- 既存ユーザーにはセグメント付き予測を適用
- 新規ユーザーにはセグメントなし予測を適用
という柔軟な運用が可能になります。
シミュレーション
さて、ここでは本記事が利用するデータのシミュレーションを実施します:
set.seed(123)
beta_seg_effect <- 1:100 |>
tibble::tibble(
seg = _
) |>
dplyr::mutate(
effect = rnorm(dplyr::n(), sd = 1)
)
beta_x <- rnorm(20, sd = 0.2)
x <- rnorm(55000 * 20) |>
matrix(ncol = 20)
seg <- sample(1:100, 55000, replace = TRUE)
y <- -20 + beta_seg_effect$effect[seg] + as.numeric(x %*% beta_x) + rnorm(55000)
シナリオを数式で表すと:
$$
y_{i} = -20 + \beta_{segment_{i}} + \sum_{k = 1}^{20} x_{i,k} \cdot \beta_{k} + \epsilon
$$
となります。
要するに、20 個のセグメントの中のどれかに観測値が属している他に、非カテゴリの連続値の特徴量が 20 個存在している状況です。
ここで、3 つのベイズモデルを作成します:
標準化ありモデル
標準化モデルでは、カテゴリ変数の標準化を実施し、予測時にカテゴリ変数の情報を使う際の誤差率とあえてカテゴリ変数の情報を使わない際の誤差率の事後分布をそれぞれ計算します。
data {
int seg_type;
int P;
int N;
array[N] int seg;
matrix[N, P] x;
vector[N] y;
int val_N;
array[val_N] int val_seg;
matrix[val_N, P] val_x;
vector[val_N] val_y;
}
parameters {
real<lower=0> rho_global;
vector<lower=0>[seg_type] rho_beta_seg;
vector<lower=0>[P] rho_beta_x;
real<lower=0> sigma;
real intercept;
vector[seg_type] beta_seg_nonnormalized;
vector[P] beta_x;
}
transformed parameters {
vector[seg_type] beta_seg;
beta_seg = beta_seg_nonnormalized - mean(beta_seg_nonnormalized);
}
model {
rho_global ~ gamma(1, 1);
rho_beta_seg ~ exponential(0.5 * (rho_global)^2);
rho_beta_x ~ exponential(0.5 * (rho_global)^2);
sigma ~ inv_gamma(5, 5);
intercept ~ normal(0, 10);
beta_seg ~ normal(0, rho_beta_seg);
beta_x ~ normal(0, rho_beta_x);
y ~ normal(intercept + beta_seg[seg] + x * beta_x, sigma);
}
generated quantities {
real mape_with_seg;
real mape_without_seg;
{
vector[val_N] ape_with_seg;
vector[val_N] ape_without_seg;
array[val_N] real predict_with_seg;
array[val_N] real predict_without_seg;
// カテゴリを含めた予測
predict_with_seg = normal_rng(intercept + beta_seg[val_seg] + val_x * beta_x, sigma);
// カテゴリをあえて無視する予測
predict_without_seg = normal_rng(intercept + val_x * beta_x, sigma);
for (i in 1:val_N){
ape_with_seg[i] = abs((val_y[i] - predict_with_seg[i])/val_y[i]);
ape_without_seg[i] = abs((val_y[i] - predict_without_seg[i])/val_y[i]);
}
mape_with_seg = mean(ape_with_seg);
mape_without_seg = mean(ape_without_seg);
}
}
標準化なしモデル
標準化なしモデルでは、カテゴリ変数の標準化を実施せずに、予測時にカテゴリ変数の情報を使う際の誤差率とあえてカテゴリ変数の情報を使わない際の誤差率の事後分布をそれぞれ計算します。
data {
int seg_type;
int P;
int N;
array[N] int seg;
matrix[N, P] x;
vector[N] y;
int val_N;
array[val_N] int val_seg;
matrix[val_N, P] val_x;
vector[val_N] val_y;
}
parameters {
real<lower=0> rho_global;
vector<lower=0>[seg_type] rho_beta_seg;
vector<lower=0>[P] rho_beta_x;
real<lower=0> sigma;
real intercept;
vector[seg_type] beta_seg;
vector[P] beta_x;
}
model {
rho_global ~ gamma(1, 1);
rho_beta_seg ~ exponential(0.5 * (rho_global)^2);
rho_beta_x ~ exponential(0.5 * (rho_global)^2);
sigma ~ inv_gamma(5, 5);
intercept ~ normal(0, 10);
beta_seg ~ normal(0, rho_beta_seg);
beta_x ~ normal(0, rho_beta_x);
y ~ normal(intercept + beta_seg[seg] + x * beta_x, sigma);
}
generated quantities {
real mape_with_seg;
real mape_without_seg;
{
vector[val_N] ape_with_seg;
vector[val_N] ape_without_seg;
array[val_N] real predict_with_seg;
array[val_N] real predict_without_seg;
// カテゴリを含めた予測
predict_with_seg = normal_rng(intercept + beta_seg[val_seg] + val_x * beta_x, sigma);
// カテゴリをあえて無視する予測
predict_without_seg = normal_rng(intercept + val_x * beta_x, sigma);
for (i in 1:val_N){
ape_with_seg[i] = abs((val_y[i] - predict_with_seg[i])/val_y[i]);
ape_without_seg[i] = abs((val_y[i] - predict_without_seg[i])/val_y[i]);
}
mape_with_seg = mean(ape_with_seg);
mape_without_seg = mean(ape_without_seg);
}
}
セグメントなしモデル
最後に、そもそもセグメントを学習の時から含めないモデルを作成し、セグメント情報のない状態で予測を実施し誤差率の事後分布を計算します。
data {
int P;
int N;
matrix[N, P] x;
vector[N] y;
int val_N;
matrix[val_N, P] val_x;
vector[val_N] val_y;
}
parameters {
real<lower=0> rho_global;
vector<lower=0>[P] rho_beta_x;
real<lower=0> sigma;
real intercept;
vector[P] beta_x;
}
model {
rho_global ~ gamma(1, 1);
rho_beta_x ~ exponential(0.5 * (rho_global)^2);
sigma ~ inv_gamma(5, 5);
intercept ~ normal(0, 10);
beta_x ~ normal(0, rho_beta_x);
y ~ normal(intercept + x * beta_x, sigma);
}
generated quantities {
real mape_without_seg;
{
vector[val_N] ape_without_seg;
array[val_N] real predict_without_seg;
predict_without_seg = normal_rng(intercept + val_x * beta_x, sigma);
for (i in 1:val_N){
ape_without_seg[i] = abs((val_y[i] - predict_without_seg[i])/val_y[i]);
}
mape_without_seg = mean(ape_without_seg);
}
}
モデル推定
まず、モデルのコンパイルを実施します:
m_init_noseg <- cmdstanr::cmdstan_model("noseg.stan")
m_init_nonnormalize <- cmdstanr::cmdstan_model("nonnormalize.stan")
m_init_normalize <- cmdstanr::cmdstan_model("normalize.stan")
次に、変分推論でモデル推定を実施します:
> m_estimate_noseg <- m_init_noseg$variational(
seed = 123,
data = list(
P = 20,
N = 50000,
x = x[1:50000,],
y = y[1:50000],
val_N = 5000,
val_x = x[50001:55000,],
val_y = y[50001:55000]
)
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.0019 seconds
1000 transitions using 10 leapfrog steps per transition would take 19 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -206152.679 1.000 1.000
200 -162516.235 0.634 1.000
300 -87251.415 0.710 0.863
400 -86350.092 0.535 0.863
500 -86267.321 0.429 0.269
600 -86255.703 0.357 0.269
700 -86201.828 0.306 0.010
800 -86214.156 0.268 0.010
900 -86235.776 0.238 0.001 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 2.4 seconds.
> m_estimate_nonnormalize <- m_init_nonnormalize$variational(
seed = 123,
data = list(
seg_type = 100,
P = 20,
N = 50000,
seg = seg[1:50000],
x = x[1:50000,],
y = y[1:50000],
val_N = 5000,
val_seg = seg[50001:55000],
val_x = x[50001:55000,],
val_y = y[50001:55000]
)
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.002925 seconds
1000 transitions using 10 leapfrog steps per transition would take 29.25 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -220923.901 1.000 1.000
200 -170889.732 0.646 1.000
300 -75231.756 0.855 1.000
400 -72283.481 0.651 1.000
500 -72173.034 0.521 0.293
600 -72107.245 0.435 0.293
700 -72006.757 0.373 0.041
800 -71942.917 0.326 0.041
900 -72042.589 0.290 0.002 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 3.1 seconds.
> m_estimate_normalize <- m_init_normalize$variational(
seed = 123,
data = list(
seg_type = 100,
P = 20,
N = 50000,
seg = seg[1:50000],
x = x[1:50000,],
y = y[1:50000],
val_N = 5000,
val_seg = seg[50001:55000],
val_x = x[50001:55000,],
val_y = y[50001:55000]
)
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.002756 seconds
1000 transitions using 10 leapfrog steps per transition would take 27.56 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -237611.985 1.000 1.000
200 -202836.757 0.586 1.000
300 -164866.740 0.467 0.230
400 -80985.213 0.609 1.000
500 -71929.499 0.513 0.230
600 -71763.744 0.428 0.230
700 -71768.896 0.367 0.171
800 -71694.419 0.321 0.171
900 -71745.621 0.285 0.126
1000 -71682.944 0.257 0.126
1100 -71737.935 0.157 0.002 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 3.5 seconds.
結果の可視化
まず、標準化ありモデルモデルの中で、セグメント情報を含める場合とあえて含めない場合の誤差率の変化を見ます:
m_estimate_normalize$draws("mape_with_seg") |>
data.frame() |>
tibble::tibble() |>
`colnames<-`("mape") |>
dplyr::mutate(
case = "seg present"
) |>
dplyr::bind_rows(
m_estimate_normalize$draws("mape_without_seg") |>
data.frame() |>
tibble::tibble() |>
`colnames<-`("mape") |>
dplyr::mutate(
case = "seg missing"
)
) |>
ggplot2::ggplot() +
ggplot2::geom_density(ggplot2::aes(x = mape, fill = case), alpha = 0.5)
当たり前ですが、セグメント情報を使わない(seg missing)の方が、誤差率が高く、予測精度が悪いです。しかも両者の差は統計的に有意です。セグメント情報があればそれをきちんと使いましょうという当たり前なことです。
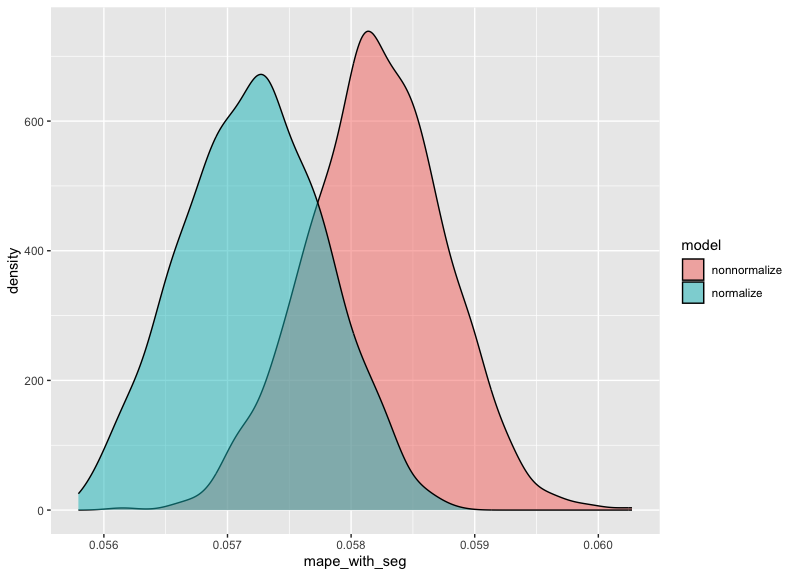
次に、標準化ありモデルと標準化なしモデルが、両方ともセグメント情報を利用して予測を実施する際の誤差率の差を可視化します:
m_estimate_nonnormalize$draws("mape_with_seg") |>
data.frame() |>
tibble::tibble() |>
dplyr::mutate(
model = "nonnormalize"
) |>
dplyr::bind_rows(
m_estimate_normalize$draws("mape_with_seg") |>
data.frame() |>
tibble::tibble() |>
dplyr::mutate(
model = "normalize"
)
) |>
ggplot2::ggplot() +
ggplot2::geom_density(ggplot2::aes(x = mape_with_seg, fill = model), alpha = 0.5)
標準化なしモデル(nonnormalize)の方が、若干誤差率が高いですが、両者の誤差率の事後分布はかなり重なっており、その違いは統計的に有意ではなく、差がないと判断した方が妥当でしょう。
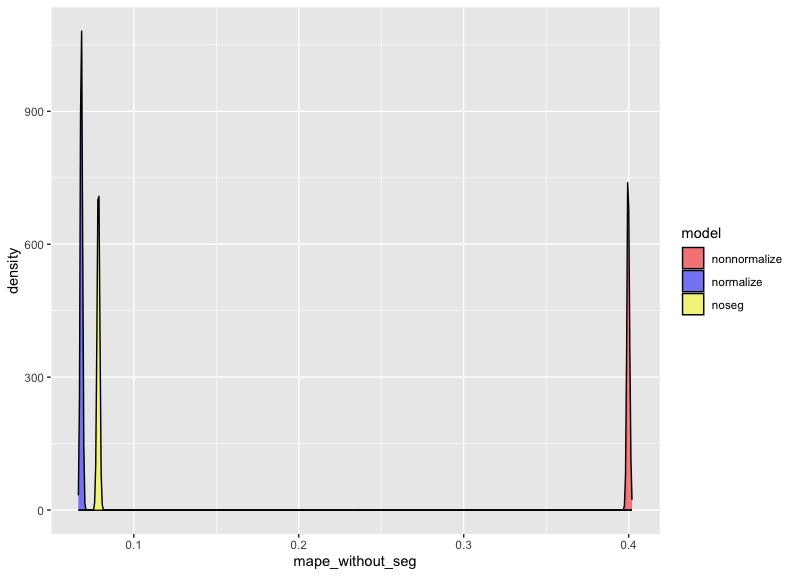
最後に、標準化ありモデル・標準化なしモデル・セグメントなしモデルの 3 つが、いずれもセグメント情報を無視して予測を行った場合に、どのような違いが生じるのかを可視化して確認しましょう:
m_estimate_nonnormalize$draws("mape_without_seg") |>
data.frame() |>
tibble::tibble() |>
dplyr::mutate(
model = "nonnormalize"
) |>
dplyr::bind_rows(
m_estimate_normalize$draws("mape_without_seg") |>
data.frame() |>
tibble::tibble() |>
dplyr::mutate(
model = "normalize"
)
) |>
dplyr::bind_rows(
m_estimate_noseg$draws("mape_without_seg") |>
data.frame() |>
tibble::tibble() |>
dplyr::mutate(
model = "noseg"
)
) |>
ggplot2::ggplot() +
ggplot2::geom_density(ggplot2::aes(x = mape_without_seg, fill = model), alpha = 0.5) +
ggplot2::scale_fill_manual(
values = c(
"normalize" = "blue",
"nonnormalize" = "red",
"noseg" = "yellow"
)
)
標準化なしモデル(nonnormalize)は、今回の設定では圧倒的に不利であることが分かります。また一見すると、「セグメントを最初から含めずに推定しているため、セグメント情報が欠落した状況に特化しているはず」と思われるセグメントなしモデル(noseg)も、誤差率としては近いものの、標準化ありモデル(normalize)がセグメント情報を使わずに予測した場合より、統計的に有意に精度が悪く、両者の誤差率の事後分布はほとんど重なりません。
nonnormalize が大きく負けた理由は明確で、カテゴリ変数の係数に「総和ゼロ」標準化を行わないと、切片の情報がカテゴリ係数に吸収されてしまうためです。結果として切片の推定が歪み、予測値に大きなバイアスが生じてしまいます。
また、noseg モデルがセグメント情報を使わない標準化ありモデルに勝てない理由は、セグメントを含めないことで結果変数のノイズが増え、セグメント以外の係数の推定精度も下がるためです。
もちろん「統計的に有意とはいえ、この程度の差ならセグメントなしに特化したモデルを作ってもいいのでは?」と考える読者もいるかもしれません。
しかし、本番環境で複数のベイズモデルを同時運用した私の経験から言わせてください:複数モデルの併存は本当にきついです。エラーの温床になるだけでなく、どのモデルがどの条件で使われるべきかが徐々に混乱し、運用負荷が跳ね上がります。さらに、特定状況に特化したモデルを増やしすぎると、MLOps ツールによってバージョン管理が崩壊しないとしても、不要な工数が確実に増えます。
したがって、もし標準化ありモデルと性能が実質的に変わらないのであれば、標準化ありモデルひとつに統一し、セグメント情報の有無に応じて予測ロジックだけを切り替える方が、本番環境での安定稼働に明らかに有利です。
結論
本記事では、カテゴリ変数に対して適切な制約(総和ゼロ制約)を課して標準化を実施する重要性を、実務で頻出する「学習時と推論時で利用できる特徴量が異なる」ケースを通じて検証しました。
シミュレーションの結果、次の 3 点が明確になりました:
-
標準化ありモデルが最も安定し、柔軟性も高い
- セグメント情報がある場合:高い精度で予測可能
- セグメント情報がない場合:セグメント係数を無視しても精度が大きく落ちない
→ 実務で必要となる「二刀流」運用に最も適している
-
標準化なしモデルは予測精度が大きく劣化する
- 切片の情報がセグメント係数に吸収される
- 推定した切片が歪み、予測が根本からバイアスされる
→ カテゴリ変数を制約なしに扱うのは危険
-
セグメントなしモデル(noseg)は意外にも弱い
- セグメントを含まないことでノイズが増加
- 他の係数の推定も不安定化し、精度で標準化ありモデルに劣る
→ 「セグメントなし運用を想定しているならセグメントなしで学習」が必ずしも正解ではない
総合的に言うと、「カテゴリ変数を総和ゼロで標準化して推定し、必要に応じてカテゴリ係数を無視して予測する」アプローチが、実務上もっとも堅牢で柔軟であり、最も高い汎用性を持つということになります。
特に近年のビジネス現場では、LLM や深層学習で生成された特徴量(例:セグメント、クラスタ、潜在表現)が推論時に必ずしも利用できない状況がますます増えています。そのような環境においても破綻しないモデル設計として、カテゴリ変数の標準化(総和ゼロ制約)は非常に有用です。
本記事が、データサイエンス現場でのモデル構築における「カテゴリ変数の扱い」の理解を深め、より柔軟で実践的なモデリング戦略の一助になれば幸いです。
最後に、私たちと一緒に働きたい方はぜひ下記のリンクもご確認ください: