はじめまして、りょーつといいます。高専出身の大学院2年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。今年度のキャチロボバトルコンテストでモデル予測制御を使用予定なのですが、その前準備としてモータのパラメータ同定の手法についてまとめたものになります。
目次
1.はじめに
2.数学的準備
3.モータの物理モデルと差分方程式
4.二次元最小二乗法によるパラメータ同定
5.実験結果
6.おわりに
7.参考文献
1. はじめに
今回の記事では、最小二乗法によるモータのパラメータ同定についてまとめます。特に理論的背景についてしっかりまとめる予定です。少し数学的な部分が出てきますが、丁寧に書くので追ってみていただけると嬉しいです。
2. 数学的準備
最小二乗法の説明時に、スカラー値をベクトルで微分するという操作が発生するため、それに関する計算式をいくつか導出しておきます。基本的に本章では後述する(3)式と(4)式の証明を行います。導出過程が気にならない方は本章を飛ばして3章に進んでください。
スカラー値をベクトルで微分するという操作は、勾配$grad$の計算と同様に、ベクトルの各成分で微分した結果をベクトルにまとめるという風に定義します。
文章で書いても分かりづらいので数式で表すと、スカラー値$\phi$をベクトル$\boldsymbol{x}$で微分した結果は以下のようになります。
\frac{d\phi}{d\boldsymbol{x}}
=
{\begin{bmatrix}
\frac{d\phi}{x_1} & \frac{d\phi}{x_2} & \cdots & \frac{d\phi}{x_n}\\
\end{bmatrix}}^T
\tag{1}
ただし
\boldsymbol{x}
=
\begin{bmatrix}
x_1 \\
x_2 \\
\vdots\\
x_n
\end{bmatrix}
\tag{2}
とします。これらを前提に以下の2つの方程式を証明します。
\frac{d}{d\boldsymbol{x}}
\big(
\boldsymbol{x}^T Q \boldsymbol{x}
\big)
=
2Q\boldsymbol{x}
\tag{3}
\frac{d}{d\boldsymbol{x}}
\big(
\boldsymbol{x}^T \boldsymbol{q}
\big)
=
\boldsymbol{q}
\tag{4}
なお、$Q$は$n\times n$の対称行列、$q$は$n$次元ベクトルです。
まず(3)式を証明します。対称行列$Q = Q^T$を以下のように定義します。
Q
=
\begin{bmatrix}
Q_{11} & Q_{12} & \cdots & Q_{1n} \\
Q_{21} & Q_{22} & \cdots & Q_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
Q_{n1} & Q_{n2} & \cdots & Q_{nn} \\
\end{bmatrix}
,
\ \ \
Q_{ij} = Q_{ji}
\tag{5}
(3)式の左辺の括弧の中身を順を追って計算すると以下のスカラー値が得られます。
\boldsymbol{x}^T Q \boldsymbol{x}
=
\begin{bmatrix}
x_{1} & x_{2} & \cdots & x_{n} \\
\end{bmatrix}
\begin{bmatrix}
Q_{11} & Q_{12} & \cdots & Q_{1n} \\
Q_{21} & Q_{22} & \cdots & Q_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
Q_{n1} & Q_{n2} & \cdots & Q_{nn} \\
\end{bmatrix}
\begin{bmatrix}
x_{1} \\
x_{2} \\
\vdots \\
x_{n} \\
\end{bmatrix}
=
\begin{bmatrix}
x_{1} & x_{2} & \cdots & x_{n} \\
\end{bmatrix}
\begin{bmatrix}
Q_{11}x_{1} + Q_{12}x_{2} + \cdots Q_{1n}x_{n}\\
Q_{21}x_{1} + Q_{22}x_{2} + \cdots Q_{2n}x_{n}\\
\vdots \\
Q_{n1}x_{1} + Q_{n2}x_{2} + \cdots Q_{nn}x_{n}\\
\end{bmatrix}
=
\begin{bmatrix}
x_{1} & x_{2} & \cdots & x_{n} \\
\end{bmatrix}
\begin{bmatrix}
\sum_{j=1}^n Q_{1j}x_{j}\\
\sum_{j=1}^n Q_{2j}x_{j}\\
\vdots \\
\sum_{j=1}^n Q_{nj}x_{j}\\
\end{bmatrix}
=
x_1 \sum_{j=1}^n Q_{1j}x_{j}\\
+
x_2 \sum_{j=1}^n Q_{2j}x_{j}\\
+
\vdots \\
+
x_n \sum_{j=1}^n Q_{nj}x_{j}\\
=
\sum_{i=1}^n x_i \bigg( \sum_{j=1}^n Q_{ij}x_{j} \bigg)
\tag{6}
(6)式のように得られたスカラー値をベクトル$\boldsymbol{x}$の$k$番目の要素で微分すると、積の微分公式より
\frac{d}{d x_k}
\big(
\boldsymbol{x}^T Q \boldsymbol{x}
\big)
=
\frac{d}{d x_k}
\Bigg(
\sum_{i=1}^n x_i \bigg( \sum_{j=1}^n Q_{ij}x_{j} \bigg)
\Bigg)
=
\sum_{j=1}^n Q_{kj}x_{j}
+
\sum_{i=1}^n x_i Q_{ik}
=
\sum_{i=1}^n Q_{ki}x_{i}
+
\sum_{i=1}^n Q_{ik} x_i
=
2\sum_{i=1}^n Q_{ki}x_{i}
\tag{7}
が得られます。最後に(1)式で定義したスカラー値のベクトルによる微分をもとに、(3)式の左辺を計算すると、右辺に一致することが分かります。
\frac{d}{d\boldsymbol{x}}
\big(
\boldsymbol{x}^T Q \boldsymbol{x}
\big)
=
2
\begin{bmatrix}
\sum_{i=1}^n Q_{1i}x_{i}\\
\sum_{i=1}^n Q_{2i}x_{i}\\
\vdots \\
\sum_{i=1}^n Q_{ni}x_{i}\\
\end{bmatrix}
=
2
\begin{bmatrix}
Q_{11} & Q_{12} & \cdots & Q_{1n} \\
Q_{21} & Q_{22} & \cdots & Q_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
Q_{n1} & Q_{n2} & \cdots & Q_{nn} \\
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\vdots \\
x_{n}\\
\end{bmatrix}
\therefore
\frac{d}{d\boldsymbol{x}}
\big(
\boldsymbol{x}^T Q \boldsymbol{x}
\big)
=
2Q \boldsymbol{x}
次に(4)式の導出を行います。$n$次元ベクトル$\boldsymbol{q}$を以下のように定義します。
\boldsymbol{q}
=
\begin{bmatrix}
q_1\\
q_2\\
\vdots \\
q_{n}\\
\end{bmatrix}
\tag{8}
このとき、(4)式の左辺の括弧の中身は以下のスカラー値になります。
\boldsymbol{x}^T \boldsymbol{q}
=
\begin{bmatrix}
x_{1} & x_{2} & \cdots & x_{n} \\
\end{bmatrix}
\begin{bmatrix}
q_1\\
q_2\\
\vdots \\
q_{n}\\
\end{bmatrix}
=
q_1 x_1 + q_2 x_2 + \cdots + q_n x_n
=
\sum_{i=1}^n q_{i} x_{i}
\tag{9}
(7)式と同様に(9)式をベクトル$\boldsymbol{x}$の$k$番目の要素$x_k$で微分すると
\frac{d}{d x_k}
\big(
\boldsymbol{x}^T \boldsymbol{q}
\big)
=
\frac{d}{d x_k}
\sum_{i=1}^n q_{i} x_{i}
=
q_k
\tag{10}
であることから、(4)式の左辺と右辺が以下のように一致することが示されます。
\therefore
\frac{d}{d \boldsymbol{x}}
\big(
\boldsymbol{x}^T \boldsymbol{q}
\big)
=
\begin{bmatrix}
q_1\\
q_2\\
\vdots \\
q_{n}\\
\end{bmatrix}
=
\boldsymbol{q}
以上により、数学的な準備が完了します。
3. モータの物理モデルと差分方程式
モータのパラメータ同定を行うために、モータの物理モデルが必要です。本章ではそれらについて軽く説明しようと思います。名前を聞いてピンとくる方もいるかもしれませんが、モータは「1次遅れ系」というモデルで近似されることが多いです。詳細な説明については過去に書いたこちらの記事や、参考文献を参照いただきたいです。1次遅れ系を仮定した場合、モータの角速度$\omega$と入力電圧$u$の間には、以下の微分方程式がなりたちます。
\frac{d\omega}{dt}
+
a \omega
=
b u
\tag{11}
なお、定数$a$と$b$はモータ固有の値であり、製品によって違う値を取ります。逆に言うと、モータのパラメータ同定とは、これら2つの値を求める操作であると言い換えることもできます。
モータの状態をサンプリング周期$\Delta t$で測定することを仮定し、(11)式を離散化してみましょう。微分を単純な差分に置き換えることで、(11)式は以下のように離散化されます。
\frac{\omega_{k+1} - \omega_k}{\Delta t}
+
a \omega_k
=
b u_k
\therefore
\omega_{k+1}
=
(1 - a \Delta t) \omega_k
+
b \Delta t\ u_k
\tag{12}
(12)式の解釈についてですが、ある時刻$k\Delta t$において角速度$\omega_k$で回転しているモータに入力$u_k$を与えると、時刻$(k+1)\Delta t$での角速度が$\omega_{k+1}$になるということを意味しています。(12)式の関係を行列にまとめると以下のようになります。
\begin{bmatrix}
\omega_1\\
\omega_2\\
\vdots \\
\omega_{n+1}\\
\end{bmatrix}
=
\begin{bmatrix}
(1 - a \Delta t) \omega_0 + b \Delta t\ u_0\\
(1 - a \Delta t) \omega_1 + b \Delta t\ u_1\\
\vdots \\
(1 - a \Delta t) \omega_n + b \Delta t\ u_n\\
\end{bmatrix}
=
\begin{bmatrix}
\omega_0 & u_0\\
\omega_1 & u_1\\
\vdots \\
\omega_n & u_n\\
\end{bmatrix}
\begin{bmatrix}
1 - a \Delta t\\
b \Delta t\\
\end{bmatrix}
\tag{13}
さらに分かりやすくまとめるために以下のように行列とベクトルを定義することで、モータの物理モデルが行列の積の形式で記述できます。
A
=
\begin{bmatrix}
\omega_0 & u_0\\
\omega_1 & u_1\\
\vdots \\
\omega_n & u_n\\
\end{bmatrix}
\tag{14}
\boldsymbol{x}
=
\begin{bmatrix}
1 - a \Delta t\\
b \Delta t\\
\end{bmatrix}
\tag{15}
\boldsymbol{b}
=
\begin{bmatrix}
\omega_1 \\
\omega_2 \\
\vdots \\
\omega_{n+1} \\
\end{bmatrix}
\tag{16}
\therefore
A\boldsymbol{x}
=
\boldsymbol{b}
\tag{17}
4. 二次元最小二乗法によるパラメータ同定
本章では3章で導出した差分方程式をもとに、最小二乗法を使用してモータのパラメータ$a$と$b$を導出する方法をまとめます。
まず、3章に登場した行列$A$、ベクトル$\boldsymbol{x}$、$\boldsymbol{b}$について考察します。モータに入力$u_k$を与えた時の角速度$\omega_{k+1}$を測定する実験を行った場合、行列$A$とベクトル行列$\boldsymbol{b}$は実験結果をまとめたものであるとみなすことができます。実験結果とモデルの間には誤差があるので、ここでは以下のベクトルの大きさが最小になるような$\boldsymbol{x}$を求めることでモータのパラメータ同定を行います。
\boldsymbol{e}
=
A\boldsymbol{x}
-
\boldsymbol{b}
\tag{18}
先に結論を提示しておくと、$\boldsymbol{e}$の大きさを最小化する$\boldsymbol{x}$は以下の式で計算できます。
\boldsymbol{x}
=
{
\big(
A^T A
\big)
}^{-1}
A^T
\boldsymbol{b}
\tag{19}
まずは(19)式を導出します。$\boldsymbol{e}$の大きさが最小化するとき、$\boldsymbol{e}^2 = \boldsymbol{e}^T \boldsymbol{e}$も最小化するため、まずは$\boldsymbol{e}^T \boldsymbol{e}$を計算します。
\boldsymbol{e}^T \boldsymbol{e}
=
{
\big(
A\boldsymbol{x} - \boldsymbol{b}
\big)
}^T
\big(
A\boldsymbol{x} - \boldsymbol{b}
\big)
=
\boldsymbol{x}^T A^T A \boldsymbol{x}
-
2 \boldsymbol{x}^T A^T \boldsymbol{b}
+
\boldsymbol{b}^T \boldsymbol{b}
\tag{20}
ここで、$A^T A$が対称行列であることに注意してください。
{(A^T A)}^T = A^T (A^T)^T = A^T A
\tag{21}
$\boldsymbol{e}$が最小(極小)になるとき、(20)式の勾配が$\boldsymbol{0}$になるため、所望の$\boldsymbol{x}$は以下の関係を満たします。なお、以下の計算には(3)式と(4)式の関係を使用しました。
\frac{d}{d\boldsymbol{x}} \big( \boldsymbol{e}^T \boldsymbol{e} \big)
=
2 A^T A \boldsymbol{x}
-
2 A^T \boldsymbol{b}
=
\boldsymbol{0}
\tag{22}
あとは対称行列$A^T A$が正則であると仮定し、(22)式を$\boldsymbol{x}$について解くことで(19)式が得られます。
A^T A \boldsymbol{x}
-
A^T \boldsymbol{b}
=
\boldsymbol{0}
A^T A \boldsymbol{x}
=
A^T \boldsymbol{b}
\therefore
\boldsymbol{x}
=
{(A^T A) }^{-1}
A^T \boldsymbol{b}
最後に、ベクトル$\boldsymbol{x}$からモータのパラメータ$a$、$b$を抽出する方法を考えます。単純な式変形により、以下の関係が成り立つことを利用します。
a = -\frac{1}{\Delta t} \times \big( (1 - a\Delta t )- 1 \big)
\tag{23}
b = \frac{1}{\Delta t} \times b\Delta t
\tag{24}
(23)式と(24)式を行列にまとめると以下のように単純化できます。
\begin{bmatrix}
a \\
b \\
\end{bmatrix}
=
\frac{1}{\Delta t}
\begin{bmatrix}
-1 & 0\\
0 & 1\\
\end{bmatrix}
\Biggl(
\begin{bmatrix}
1 - a\Delta t\\
b\Delta t\\
\end{bmatrix}
-
\begin{bmatrix}
1 \\
0 \\
\end{bmatrix}
\Biggr)
\tag{25}
最後に本記事の内容をまとめるとモータのパラメター$a$と$b$は以下の計算により同定できます。
\begin{bmatrix}
a \\
b \\
\end{bmatrix}
=
C\big({(A^T A) }^{-1}
A^T \boldsymbol{b} - \boldsymbol{d} \big)
\tag{26}
ただし
C
=
\frac{1}{\Delta t}
\begin{bmatrix}
-1 & 0\\
0 & 1\\
\end{bmatrix}
\tag{27}
\boldsymbol{d}
=
\begin{bmatrix}
1 \\
0 \\
\end{bmatrix}
\tag{28}
です。
5. 実験結果
本章では(26)式を使ってパラメータ同定をした結果についてまとめます。Arduinoを使ったので、入力$u$には電圧値ではなく、デューティー比$\eta \in \mathbb{Z}, (-256 < \eta < 256)$を使用しています。実験には以下の4種類の入力を使用しました。
\eta_1
=
200\sin{(10t + \alpha_1)}
\tag{29}
\eta_2
=
200\sin{(20t + \alpha_2)}
\tag{30}
\eta_3
=
200\sin{(30t + \alpha_3)}
\tag{31}
\eta_4
=
200\sin{(40t + \alpha_4)}
\tag{32}
それぞれの入力における$\eta$と$\omega$[rad/s]の関係について図1~図4にまとめました。なお、角速度$omega$[rad/s]はモータに取り付けられた16667[ppr]のロータリーエンコーダで取得した角度を完全微分した値を用いています。

図1 $\eta_1$と$\omega$[rad/s]の関係
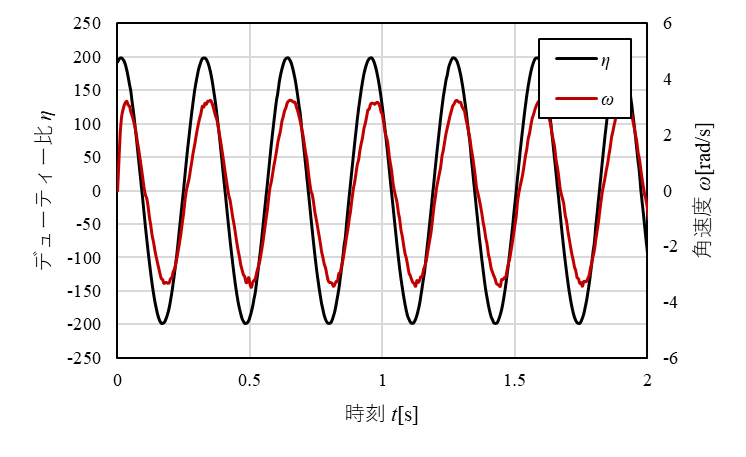
図2 $\eta_2$と$\omega$[rad/s]の関係

図3 $\eta_3$と$\omega$[rad/s]の関係
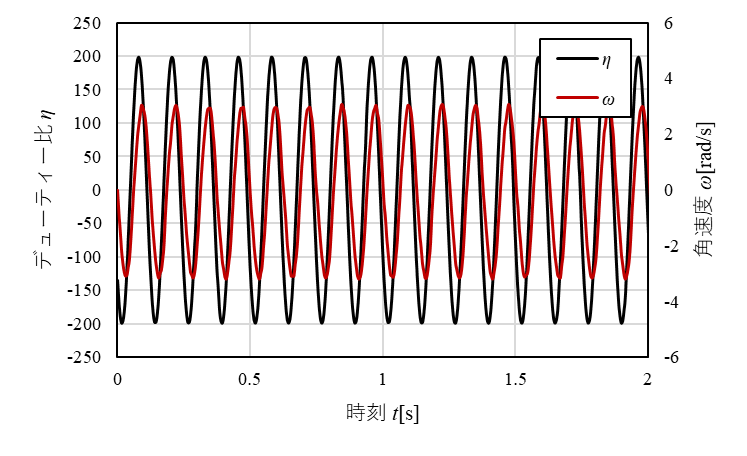
図4 $\eta_4$と$\omega$[rad/s]の関係
図1~図4のように計測した値をそれぞれ行列にまとめ、(26)式を計算し、パラメータ$a$と$b$を求めました。行列の計算にはMatlab R2023aを使用しました。
各入力におけるパラメータ$a$と$b$の計算結果を表1にまとめました。ほとんど誤差がなく、かなり高い精度でパラメータ同定できていることが分かります。
6. おわりに
本稿では、差分方程式と最小二乗法を用いたモータのパラメータ同定についてまとめました。来週は、同定したパラメータ$a$と$b$を用いて1ステップのモデル予測制御(MPC)の実装についてまとめたいと考えています。
今週も最後まで読んでいただききありがとうございました。
7. 参考文献
① 川田昌克:物理法則に基づくモデリング、システム/制御/情報、Vol56、No.4、pp.166-169 (2012)
② 川田昌克:MATLAB/Simulinkによる現代制御入門、森北出版 (2015)
③ 高校数学の美しい物語:最小二乗法の行列表現、最終閲覧日2025/07/19
